京都府立医科大学 2024年 問題2
$以下のような硬貨投げを行う。$
$1\ 枚の硬貨を投げて裏が出たら硬貨投げを終了し、表が出たら \ 1\ 枚の硬貨を加え \ 2\ 枚の硬貨を同時に投げる。$
$2\ 枚の硬貨のうち \ 1\ 枚でも裏が出たら硬貨投げを終了し、全部が表ならば \ 1\ 枚の硬貨を加え \ 3\ 枚の硬貨を同時$
$に投げる。3\ 枚のうち \ 1\ 枚でも裏が出たら硬貨投げを終了し、全部が表ならば \ 1\ 枚の硬貨を加え \ 4\ 枚の硬貨を$
$同時に投げる。以下同様にして全部が表ならば \ 1\ 枚の硬貨を加えて硬貨投げを続ける。$
$1\ 枚の硬貨から始めて、硬貨が \ n\ 枚のときに硬貨投げが終了する確率を \ p_n \ \ (n \geqq 1)\ \ とする。$
$(1)\ \ p_n \ を \ n\ を用いて表せ。$
\[(2)\ \ 無限級数の和 \ \ \sum_{n=1}^{\infty} p_n \ \ を求めよ。\]
frac$\quad 用いてよい。$
(1)
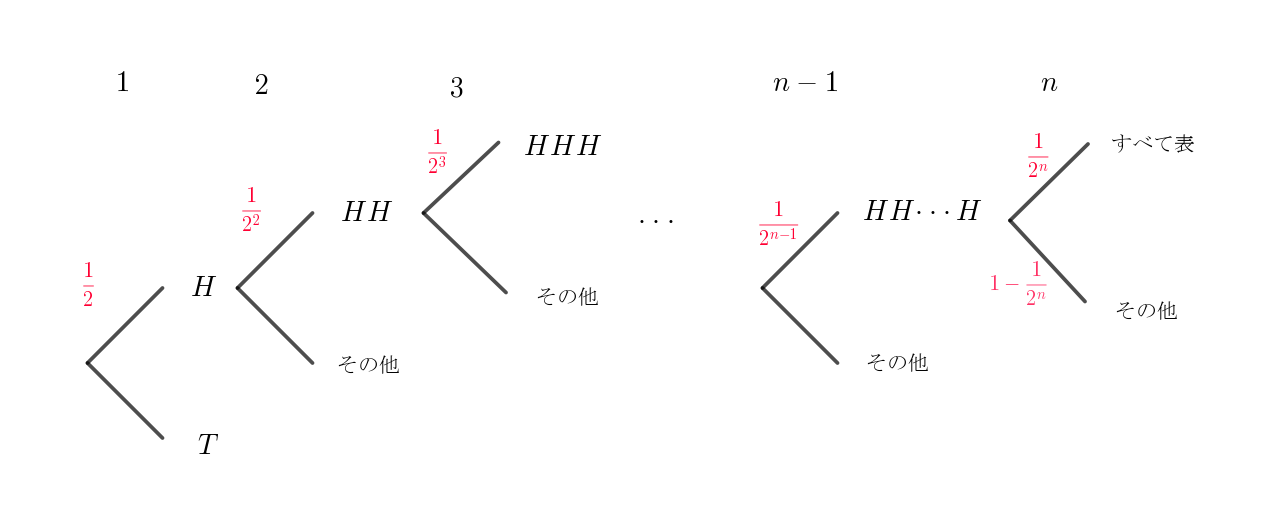
$(n-1)\ 枚までは連続してすべて表が出て、n\ 枚のとき初めて少なくとも \ 1\ 枚裏が出る場合であるから$
\begin{eqnarray*} p_n &=&\cfrac{1}{2} \times \cfrac{1}{2^2} \times \cdots \times \cfrac{1}{2^{n-1}} \times \big(1-\cfrac{1}{2^n}\big)\\ \\ &=&\cfrac{1}{2^{1+2+\cdots + (n-1)}} \times \big(1-\cfrac{1}{2^n}\big)\\ \\ &=&\cfrac{1}{2^{1+2+\cdots + (n-1)}} - \cfrac{1}{2^{1+2+\cdots + n}} \\ \\ &=&\cfrac{1}{2^{\scriptsize{\dfrac{(n-1)n}{2}}}} - \cfrac{1}{2^{\scriptsize{\dfrac{n(n+1)}{2}}}} \\ \\ \end{eqnarray*}
(2)
\begin{eqnarray*} \sum_{k=1}^n p_k &=&\sum_{k=1}^n \Big(\cfrac{1}{2^{\scriptsize{\dfrac{(k-1)k}{2}}}} - \cfrac{1}{2^{\scriptsize{\dfrac{k(k+1)}{2}}}}\Big) \\ \\ &=&\Big(\cfrac{1}{2^{\scriptsize{\dfrac{0 \times 1}{2}}}} - \cfrac{1}{2^{\scriptsize{\dfrac{1 \times 2}{2}}}}\Big)+ \Big(\cfrac{1}{2^{\scriptsize{\dfrac{1 \times 2}{2}}}} - \cfrac{1}{2^{\scriptsize{\dfrac{2 \times 3}{2}}}}\Big)+ \cdots + \Big(\cfrac{1}{2^{\scriptsize{\dfrac{(n-1)n}{2}}}} - \cfrac{1}{2^{\scriptsize{\dfrac{n(n+1)}{2}}}}\Big) \\ \\ &=&\cfrac{1}{2^{\scriptsize{\dfrac{0 \times 1}{2}}}} - \cfrac{1}{2^{\scriptsize{\dfrac{n(n+1)}{2}}}} \\ \\ &=&1 - \cfrac{1}{2^{\scriptsize{\dfrac{n(n+1)}{2}}}} \end{eqnarray*}
\[n \longrightarrow \infty \quad のとき \quad \cfrac{1}{2^{\scriptsize{\dfrac{n(n+1)}{2}}}} \longrightarrow 0 \quad だから \quad \sum_{n=1}^{\infty} p_n=1\]
(3)
\[P_n=\sum_{k=1}^n p_k \ \ とおくと\]
$p_1=1-\cfrac{1}{2}=\cfrac{1}{2}=0.5$
$p_3=\cfrac{1}{2^3} - \cfrac{1}{2^6}=\cfrac{1}{8}-\cfrac{1}{64}=\cfrac{7}{64}=0.109 $
$p_n > 0 \quad だから$
$P > p_1+p_3 =0.5+0.109=0.609 > 0.6$
$また$
$p_5=\cfrac{1}{2^{10}} - \cfrac{1}{2^{15}}=\cfrac{1}{1024}-\cfrac{1}{1024 \times 32} < \cfrac{1}{1000}=0.001$
$p_7=\cfrac{1}{2^{21}} - \cfrac{1}{2^{28}}$
$2^{21}=2^{10} \times 2^{10} \times 2=1024 \times 1024 \times 2> 10^6 \times 2 >10^6 \quad だから$
$p_7 < \cfrac{1}{2^{21}} < 10^{-6}$
\[p_{2n-1}\ \ は正で、単調減少、\sum_{n=1}^{\infty} p_{2n-1}\ \ は収束することから\]
$p_7+p_9+ \cdots \ \ =K\ \ (定数) \ \ は小数第 \ 2\ 位に影響を与えないほど小さい。$
\begin{eqnarray*} P &=&p_1+p_3+p_5 +K\\ \\ &<&0.5+0.109+0.001 +K\\ \\ &=&0.610+K\\ \\ &<&0.62 \end{eqnarray*}
$後半が数学的論理展開として納得がいかない場合は次のように考えるとよいでしょう。$
$(別解)$
\[Q=\sum_{n=1}^{\infty} p_{2n} \quad とおく\]
\[(2)より \quad \sum_{n=1}^{\infty} p_n \ \ は収束し、\sum_{n=1}^{\infty} p_{2n-1} \quad も収束するから \ Q\ も収束し、P+Q=1\ \ が成りたつ。\]
$p_2=\cfrac{1}{2} \times \big(1-\cfrac{1}{2^2}\big)=\cfrac{3}{8}=0.375 $
$p_4=\cfrac{1}{2} \times \cfrac{1}{2^2} \times \cfrac{1}{2^3} \times \big(1-\cfrac{1}{2^4}\big)=\cfrac{15}{2^{10}} =\cfrac{15}{1024}=0.0146 $
$Q >p_2+p_4=0.375 + 0.0146=0.3896$
$P=1-Q<1-0.3896=0.6104 < 0.62$
メインメニュー に戻る