神戸大学(理系) 2025年 問題5
$連続関数 \ f(x)\ は \ x \geqq 0\ で \ f(x) \geqq 0 \ を満たし、x > 0 \ で微分可能であり、その導関数 \ f'(x) \ は連続であると$
$する。t \geqq 1 \ を満たす \ t\ に対して、原点 \ O\ と点 \ P(t,\ f(t))\ の距離を \ g(t)\ とする。また、t > 1\ を満たす \ t\ に$
$対して、y=f(x) \ \ (1 \leqq x \leqq t)\ \ で表される曲線の長さを \ h(t)\ とし、t=1\ のときは \ h(1)=0 \ とする。以下の$
$問に答えよ。$
$(1)\ \ t > 1 \ とする。開区間\ (1,\ t)\ で常に\ \ f(x)-xf'(x)=0 \ \ が成り立つならば、閉区間 \ [1,\ t]\ で \ \ \dfrac{f(x)}{x} \ \ は$
$\quad 定数であることを示せ。$
$(2)\ \ t \geqq 1 \ を満たす任意の \ t\ に対して、g(t)=h(t)+2 \ \ が成り立つとする。このとき、f(1)\ の値を求めよ。$
$\quad また、t \geqq 1 \ のとき \ f(t)\ を \ t\ を用いて表せ。$
(1)
$\cfrac{d}{dx} \cfrac{f(x)}{x}=\cfrac{xf'(x)-f(x)}{x^2} =0$
$よって、開区間\ (1,\ t)\ で常に\ \ f(x)-xf'(x)=0 \ \ が成り立つならば、閉区間 \ [1,\ t]\ で \ \ \dfrac{f(x)}{x} \ \ は定数である。$
$(別解)$
$f(x)-xf'(x)=0 \ \ より \ \ \cfrac{f'(x)}{f(x)}=\cfrac{1}{x}$
$両辺 \ x\ で積分して \quad \log f(x)=\log x +\log C \quad ただし \ \ \log C\ は積分定数$
$よって \quad f(x)=Cx \quad すなわち \quad \cfrac{f(x)}{x}=C$
(2)
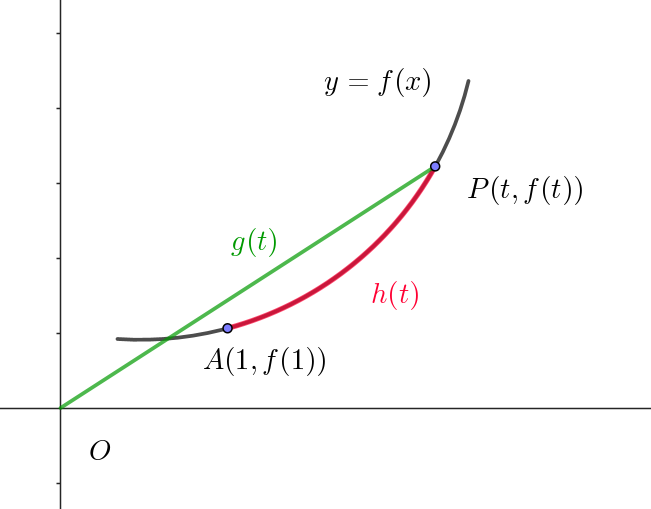
$\quad g(t)=\sqrt{t^2+(f(t))^2} \hspace{7.5em}①$
$h(t)\ は曲線 \ \ y=f(x) \ \ (1 \leqq x \leqq t)\ \ の長さだから$
\[\quad h(t)=\int_1^t \sqrt{1+(f'(x))^2}dx \hspace{5em}②\] $与えられた条件より$
$\quad g(t)=h(t)+2 \hspace{10em}③$
$①、②を③に代入して$
\[\sqrt{t^2+(f(t))^2}=\int_1^t \sqrt{1+(f'(x))^2}dx +2 \hspace{5em} ④\] $この式で \ t=1\ とおくと$
\[\sqrt{1+(f(1))^2}=\int_1^1 \sqrt{1+(f'(x))^2}dx +2 \] $\sqrt{1+(f(1))^2}=2$
$(f(1))^2=3$
$f(x) \geqq 0 \ \ だから \ \ f(1)=\sqrt{3}$
$④を \ t\ で微分して $
$\cfrac{t+f(t)f'(t)}{\sqrt{t^2+(f(t))^2}}=\sqrt{1+(f'(t))^2}$
$t+f(t)f'(t) =\sqrt{1+(f'(t))^2} \sqrt{t^2+(f(t))^2} $
$両辺平方して$
$\big(t+f(t)f'(t)\big)^2 =\big(1+(f'(t))^2 \big)\big(t^2+(f(t))^2\big)$
$展開してまとめると$
$(f(t))^2-2tf(t)f'(t)+t^2(f'(t))^2=0$
$\big(f(t)-tf'(t) \big)^2=0$
$よって \quad f(t)-tf'(t)=0$
$(1)より \ \ \cfrac{f(t)}{t}\ \ は定数だからこれを \ C\ とおくと$
$\cfrac{f(t)}{t} =C$
$f(t)=Ct$
$f(1)=\sqrt{3} \ \ だから \ \ C=\sqrt{3}$
$\therefore \ \ f(t)=\sqrt{3}t$
メインメニュー に戻る