神戸大学(理系) 2025年　問題4


$x,\ y\ を実数とする。座標空間に \ 3\ 点 \ A(-4,\ -1,\ 0),\ B(-3,\ 0,\ -1),\ P(s,\ t,\ -2s+t-1)\ がある。$
$以下の問に答えよ。$
$(1)\ \ 3\ 点 \ A,\ B,\ P\ は一直線上にないことを示せ。$
$(2)\ \ 点 \ P\ から直線 \ AB\ に下した垂線を \ PHと\ する。点Hの座標を \ s\ を用いて表せ。$
$(3)\ \ s,\ t\ が変化するとき、三角形 \ ABP\ の面積の最小値を求めよ。$


(1)


$\vec{AB}=\vec{OB}-\vec{OA}=(-3,\ 0,\ -1)- (-4,\ -1,\ 0)=(1,\ 1,\ -1)$

\begin{eqnarray*} \vec{AP} &=&\vec{OP}-\vec{OA}\\ \\ &=&(s,\ t,\ -2s+t-1)- (-4,\ -1,\ 0)\\ \\ &=&(s+4,\ t+1,\ -2s+t-1) \end{eqnarray*} $3\ 点 \ A,\ B,\ P\ が一直線上にあれば、\vec{AP}=k\vec{AB}\ \ をみたす実数 \ k\ が存在するから$

$(s+4,\ t+1,\ -2s+t-1)=k(1,\ 1,\ -1)$

\[ \hspace{1em} \left\{ \begin{array}{l} s+4=k \hspace{9em}①\\ t+1=k \hspace{9em}②\\ -2s+t-1=-k \hspace{5.3em}③\\ \end{array} \right. \]
$①、②より \ \ s=k-4,\ \ t=k-1 \quad これらを③に代入して$

$-2(k-4)+(k-1)-1=-k$

$-k+6=-k$

$これをみたす実数 \ k\ は存在」しない。$

$よって、3\ 点 \ A,\ B,\ P\ は一直線上にない。$


(2)

　

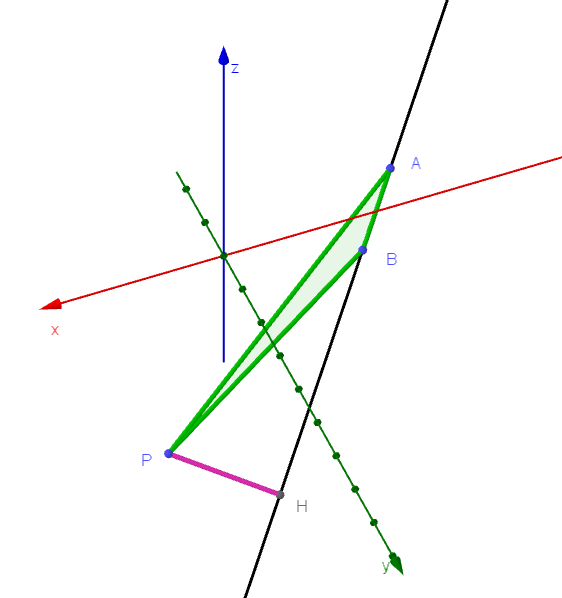
$点 \ H\ は直線 \ AB\ 上にあるから \ \ \vec{AH}=u\vec{AB}\ \ を満たす実数 \ u\ が存在する。$

$\vec{OH}-\vec{OA}=u\vec{AB}\ \ より$

$\vec{OH}=\vec{OA}+u\vec{AB}=(-4,\ -1,\ 0)+(u,\ u,\ -u)=(u-4,\ u-1,\ -u)$

\begin{eqnarray*} \vec{PH} &=&\vec{OH}-\vec{OP}\\ \\ &=&(u-4,\ u-1,\ -u) - (s,\ t,\ -2s+t-1)\\ \\ &=&(u-s-4,\ u-t-1,\ -u+2s-t+1) \end{eqnarray*}
$\vec{PH} \perp \vec{AB} \quad だから$

$(u-s-4,\ u-t-1,\ -u+2s-t+1) \cdot (1,\ 1,\ -1)=0$

$(u-s-4)+(u-t-1)-(-u+2s-t+1)=0$

$u=s+2$

$\vec{OH}=(u-4,\ u-1,\ -u)=(s-2,\ s+1,\ -s-2)$

$よって \quad H(s-2,\ s+1,\ -s-2)$


(3)


$\triangle ABP=\cfrac{1}{2} \times AB \times PH =\cfrac{\sqrt{3}}{2}PH \ \ だから \ PH\ が最小のとき、\triangle ABP \ は最小となる。$

$\vec{PH}=(u-s-4,\ u-t-1,\ -u+2s-t+1)\ \ において　垂直条件から \quad u=s+2 \ \ だから$

$\vec{PH}=(-2,\ s-t+1,\ s-t-1)$

$PH^2=|\vec{PH}|^2=(-2)^2 +(s-t+1)^2+(s-t-1)^2=2(s-t)^2+6$

$よって \quad PH\ は \ s=t \ のとき \ \ 最小値 \ \ \sqrt{6}\ \ をとる。$

$ゆえに、三角形 \ ABP\ の面積は、s=t \ のとき最小となり、$

$最小値は \quad \cfrac{1}{2} \times \sqrt{3} \times \sqrt{6}=\cfrac{3\sqrt{2}}{2}$


ページの先頭へ↑




メインメニュー　に戻る