神戸大学(理系) 2025年　問題3


$媒介変数 \ \theta \ を用いて \ \ x=\sin \theta,\ \ y=\cos \theta +|\sin \theta | \ \ (0 \leqq \theta \leqq 2\pi)\ \ で表される曲線を \ C\ とする。$
$以下の問に答えよ。$
$(1)\ \ 曲線 \ C\ の概形をかけ。$
$(2)\ \ 曲線 \ C\ で囲まれた部分の面積を求めよ。$


$◎\ \ 類似の問題が \ 2023\ 年度にも出題されています。($2023神戸大学(理系)問5$)をご覧ください。$

(1)

\[ 0 \leqq \theta \leqq \pi \ \ に対して、w=2\pi - \theta \ \ とおくと \quad \begin{array}{c|c} \theta & 0 \rightarrow \pi \\ \hline w & 2\pi \rightarrow \pi \\ \end{array} \] $x'=\sin w =\sin(2\pi -\theta)=-\sin \theta=-x$

$y'=\cos w + |\sin w |=\cos(2\pi \theta)+ |\sin(2\pi -\theta)|=\cos \theta +|\sin \theta|=y$

$よって、グラフは \ y\ 軸に関して対称である。$

　

(i)$\ \ 0 \leqq \theta \leqq \dfrac{\pi}{2} \ \ のとき$

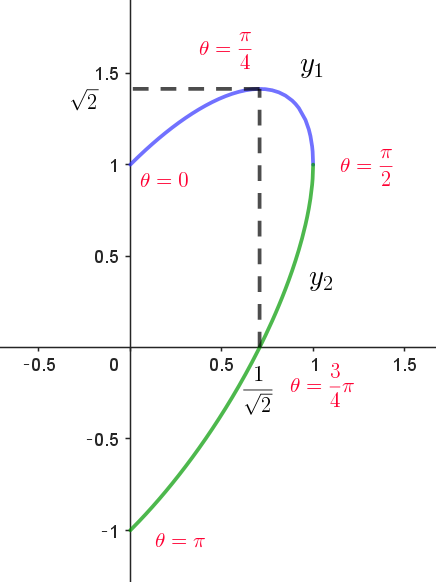
$\quad \sin \theta \geqq 0 ,\quad \cos \theta \geqq 0$

$\quad \cos ^2\theta=1-\sin ^2\theta=1-x^2 \qquad \therefore \ \ \cos \theta=\sqrt{1-x^2}$

$\quad 0 \leqq x \leqq 1 $

$\quad y_1=\cos \theta + \sin \theta=\sqrt{1-x^2}+x$

$\quad y_1'=-\cfrac{x}{\sqrt{1-x^2}}+1=\cfrac{\sqrt{1-x^2}-x}{\sqrt{1-x^2}}$

$\quad y'_1=0 \ \ より \ \ \sqrt{1-x^2}=x \qquad 1-x^2=x^2 \qquad \therefore \ \ x=\cfrac{1}{\sqrt{2}}$
\[ \quad \begin{array}{c||c|c|c|c|c} x & 0 & \cdots & \dfrac{1}{\sqrt{2}} & \cdots & 1\\ \hline y_1'& & + & 0 & - & \\ \hline y_1& & \nearrow & 極大 & \searrow & \\ \end{array} \]
$\quad x=\cfrac{1}{\sqrt{2}}\ \ で極大値 \ \ y_1=\sqrt{1-\dfrac{1}{2}}+\cfrac{1}{2}=\sqrt{2}\ \ をとる。$

$\quad x=0 \ \ のとき \ \ y_1=1,\quad x=1\ \ のとき \ \ y_1=1$

　

(ii)$\ \ \dfrac{\pi}{2} \leqq \theta \leqq \pi \ \ のとき$

$\quad \sin \theta \geqq 0 ,\quad \cos \theta \leqq 0$

$\quad \cos ^2\theta=1-\sin ^2\theta=1-x^2 \qquad \therefore \ \ \cos \theta=-\sqrt{1-x^2}$

$\quad 0 \leqq x \leqq 1 $

$\quad y_2=\cos \theta + \sin \theta=- \sqrt{1-x^2}+x$

$\quad y_2'=\cfrac{x}{\sqrt{1-x^2}}+1>0 $

$\quad したがって \ y_2 \ はこの区間で単調増加$

$\quad x=0 \ \ のとき \ \ y_2=-1 ,\quad x=1\ \ のとき \ \ y_2=1$

$\quad x\ 軸との交点は \quad \sqrt{1-x^2}=x \ \ より \ \ x=\cfrac{1}{\sqrt{2}}$


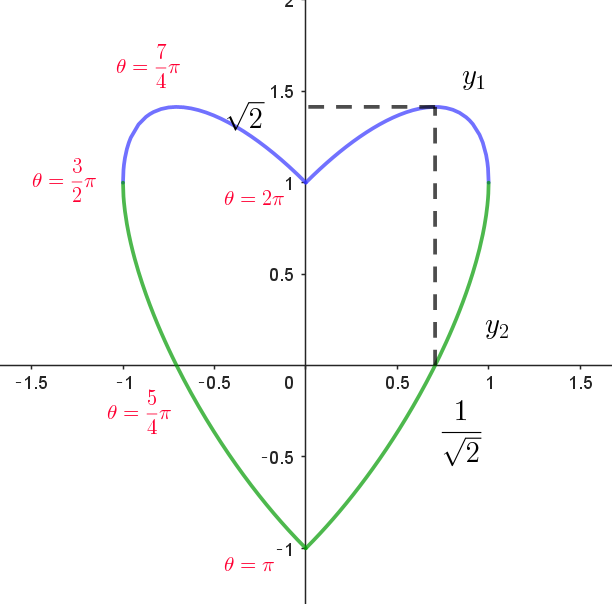
(i),(ii)$ \ \ のグラフを \ y\ 軸に関して対称移動したグラフをあわせると曲線 \ C\ となる。$


(2)


$曲線 \ C\ は \ y\ 軸に関して対称だから \ \ x \geqq 0 \ \ の部分の面積 \ T\ を求める。$

$y_1=\sqrt{1-x^2}+x,\quad y_2=-\sqrt{1-x^2}+x \quad だから$

\begin{eqnarray*} T &=&\int_0^1(y_1-y_2)dx\\ \\ &=&\int_0^1\big\{(\sqrt{1-x^2}+x)-(-\sqrt{1-x^2}+x)\big\}dx\\ \\ &=&\int_0^12\sqrt{1-x^2}dx \hspace{5em}(定積分は半径1の円の面積の\dfrac{1}{4})\\ \\ &=&2 \times \dfrac{1}{4} \times \pi \times 1^2 \\ \\ &=&\dfrac{\pi}{2} \end{eqnarray*}
$よって求める面積 \ S\ は \quad S=~2T=\pi$


$(別解)$

$曲線が媒介変数表示だから \ \theta \ で積分する。$

\begin{eqnarray*} T &=&\int_0^1(y_1-y_2)dx\\ \\ &=&\int_0^{\scriptsize{\dfrac{\pi}{2}}}(\cos \theta +\sin \theta)\cos \theta d\theta - \int_{\pi}^{\scriptsize{\dfrac{\pi}{2}}}(\cos \theta +\sin \theta)\cos \theta d\theta\\ \\ &=&\int_0^{\scriptsize{\dfrac{\pi}{2}}}(\cos \theta +\sin \theta)\cos \theta d\theta + \int_{\scriptsize{\dfrac{\pi}{2}}}^{\pi}(\cos \theta +\sin \theta)\cos \theta d\theta\\ \\ &=&\int_0^{\pi}(\cos \theta +\sin \theta)\cos \theta d\theta\\ \\ &=&\int_0^{\pi}(\cos ^2\theta +\sin \theta \cos \theta) d\theta\\ \\ &=&\int_0^{\pi}(\dfrac{1}{2}(1+\cos 2\theta ) + \dfrac{1}{2}\sin 2\theta ) d\theta\\ \\ &=&\dfrac{1}{2}\big[\theta + \dfrac{1}{2}\sin 2\theta - \dfrac{1}{2}\cos 2\theta \big]_0^{\pi}\\ \\ &=&\dfrac{1}{2}(\big[\theta + \dfrac{1}{2}\sin 2\theta - \dfrac{1}{2}\cos 2\theta \big]_0^{\pi}\\ \\ &=&\cfrac{\pi}{2} \end{eqnarray*}

ページの先頭へ↑




メインメニュー　に戻る