神戸大学(理系) 2025年　問題2


$実数 \ a\ に対して、a\ を超えない最大の整数を \ k\ とするとき、a-k\ を \ a\ の小数部分という。n\ を自然数とし、$
$a_n=\sqrt{n^2+1}-n \ \ とおく。以下の問に答えよ。$
$(1)\ \ 0 < a_n < 1 \ \ が成り立つことを示せ。$
$(2)\ \ b_n \ を \ (3n-\dfrac{1}{a_n}) \ の小数部分とする。b_n \ を \ n\ を用いて表せ。$
$(3)\ \ b_n \ を(2) で定めたものとする。m, \ n\ を異なる \ 2\ つの自然数とするとき、a_m +b_n \ne 1 \ \ であることを示せ。$


(1)


(i)$\ \ 自然数 \ n\ に対して \ \ n^2+1 > n^2 \ \ だから、両辺の平方根をとって \quad \sqrt{n^2+1} > n$

$\therefore \ \ a_n=\sqrt{n^2+1}-n > 0$

(ii) \begin{eqnarray*} & &1-a_n\\ \\ &=&1-(\sqrt{n^2+1}-n)\\ \\ &=&n+1-\sqrt{n^2+1}\\ \\ &=&\cfrac{(n+1)^2-(n^2+1)}{(n+1)+\sqrt{n^2+1}}\\ \\ &=&\cfrac{2n}{n+1+\sqrt{n^2+1}}\\ \\ &>&0 \end{eqnarray*} $\therefore \ \ a_n < 1$

(i),(ii)$\ \ より \quad 0 < a_n < 1$


(2)

\begin{eqnarray*} & &3n-\dfrac{1}{a_n}\\ \\ &=&3n-\dfrac{1}{\sqrt{n^2+1}-n}\\ \\ &=&3n-(\sqrt{n^2+1}+n)\\ \\ &=&n-(\sqrt{n^2+1}-n)\\ \\ &=&n-a_n\\ \\ &=&(n-1)+(1-a_n) \end{eqnarray*}
$(1)より \ \ 0 < a_n < 1 \ \ だから \quad 0 < 1-a_n < 1$

$n-1 \ は自然数だから、1-a_n \ \ は小数部分となり$

$b_n=1-a_n=1-(\sqrt{n^2+1}-n)=n+1-\sqrt{n^2+1}$


(3)


$(2)より$

$a_m+b_n-1=a_m+(1-a_n)-1=a_m-a_n$

$ここで、x\ を実数として、関数 \ f(x)=\sqrt{x^2+1}-x \ \ (x > 0)$

$を考える。$

$f'(x)=\cfrac{x}{\sqrt{x^2+1}}-1=\cfrac{x-\sqrt{x^2+1}}{\sqrt{x^2+1}} < 0$

$よって \ \ f(x)\ は単調減少で, \quad f(x) > 0,\quad f(0)=1 \quad だから$

$グラフは右図のとおり$

　

$グラフ上に点 \ M(m.\ a_m),\ \ N(n,\ a_n)\ \ をとると$

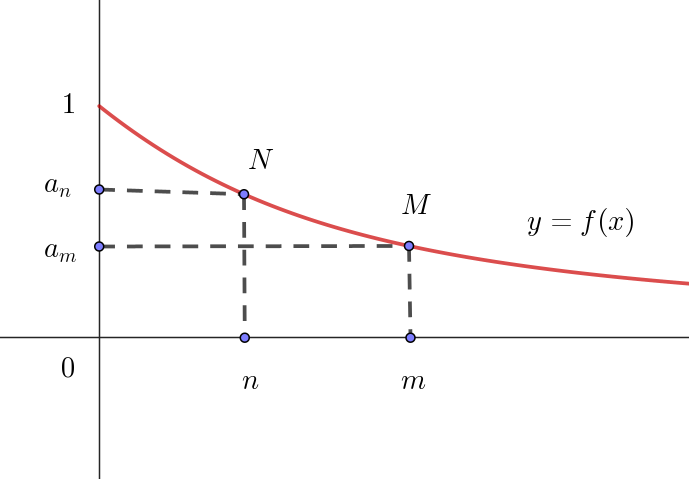
\[ \hspace{1em} \left\{ \begin{array}{l} a_m < a_n \hspace{5em}(n < m \ \ のとき)\\ a_m = a_n \hspace{5em}(n = m \ \ のとき)\\ a_m > a_n \hspace{5em}(n > m \ \ のとき)\\ \end{array} \right. \]
$したがって \quad m \ne n \ \ ならば \quad a_m \ne a_n$

$すなわち \quad m, \ n\ が異なる \ 2\ つの自然数ならば、a_m +b_n \ne 1 \ \ である。$


ページの先頭へ↑



メインメニュー　に戻る