神戸大学(理系) 2025年　問題1


$k\ を実数とする。f(x)\ と \ g(x)\ を \ \ f(x)=|x^3-x|,\ \ g(x)=k(x+1) \ \ とおき、曲線 \ y=f(x)\ を \ C,$
$直線 \ y=g(x)\ を \ \ell \ \ とする。以下の問に答えよ。$
$(1)\ \ 曲線 \ C\ の概形をかけ。ただし、関数 \ f(x)\ の極大値を調べる必要はない。$
$(2)\ \ 曲線 \ C\ と直線 \ \ell \ がちょうど \ 4\ つの共有点をもつような \ k\ の値を求めよ。$


(1)


$x^3-x=x(x+1)(x-1) \ \ より$

$y=x^3-x \ \ のグラフは \ x\ 軸と \ (-1,\ 0),\ \ (0,\ 0),\ \ (1,\ 0) \ \ で交わる \ 3\ 次関数のグラフであり、$

$y=x^3-x \ \ は奇関数だからグラフは原点について対称である。$

　

$f(x)=|x^3-x| \ \ のグラフは \ \ y=x^3-x \ \ の負の部分を$

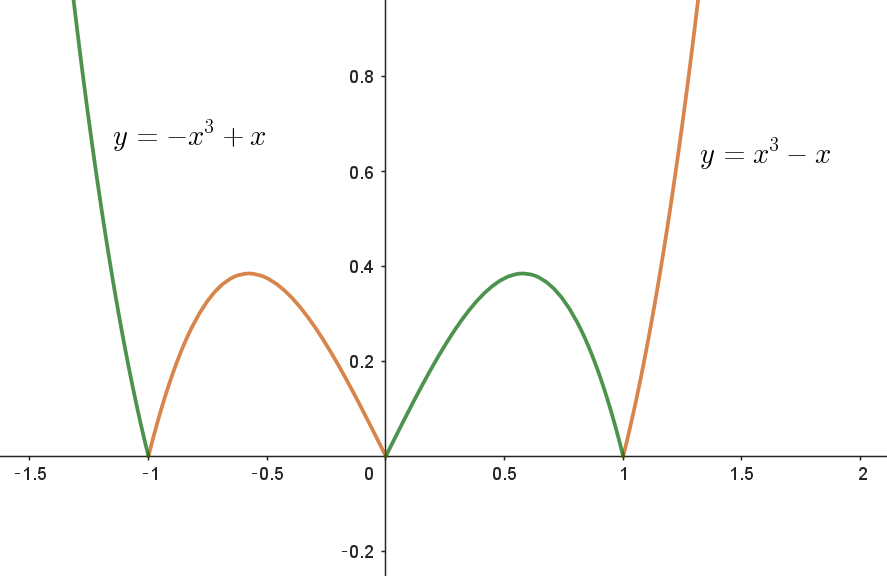
$x\ 軸に関して折り返したものである。$

$すなわち$
\[ \hspace{1em} |x^3-x|= \left\{ \begin{array}{l} -x^3+x \qquad (x \leqq -1,\ \ 0 \leqq x \leqq 1)\\ x^3-x \qquad \ \ (-1 \leqq x \leqq 0 , \ \ x \geqq 1)\\ \end{array} \right. \] $f(-x)=f(x) \ \ だから \ \ y＝f(x)\ は偶関数で、グラフは \ y\ 軸について対称である。$

$これらのことから、y=f(x) \ \ のグラフは右図のとおり$


(2)

　

$\ell : y=g(x)=k(x+1)\ \ は \ A(-1,\ 0)\ を通る傾き \ k\ の直線である。$

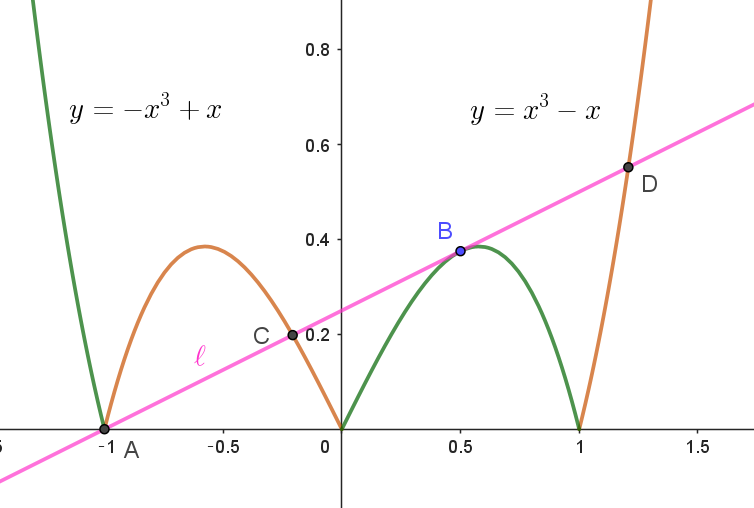
$曲線 \ C\ と直線 \ \ell \ がちょうど \ 4\ つの共有点をもつのは$

$右図のように、\ell \ が \ C\ に区間 \ (0,\ 1)\ の部分で接する場合である。$

$区間 \ (0,\ 1)\ では、C\ は \ \ f(x)=-x^3+x \ \ だから \ \ f'(x)=-3x^2+1$

$接点を \ B(a,\ -a^3+a) \ \ とおくと、B\ における接線は$

$y=(-3a^2+1)(x-a)-a^3+a \hspace{5em}①$

$これが点 \ A(-1,\ 0)\ \ を通るから$

$0=(-3a^2+1)(-1-a)-a^3+a$

$2a^3+3a^2-1=0$

$a=-1 \ \ を代入すると \ \ 左辺=0\ \ となるので \ \ (a+1)\ を因数にもつ。$

$割り算を行ってっ商を求めると$

$(a+1)(2a^2+a-1)=0$

$(a+1)^2(2a-1)=0$

$0 < a < 1 \ \ だから \ \ a=\cfrac{1}{2}$

$このとき \quad -a^3+a=-\cfrac{1}{8}+\cfrac{1}{2}=\cfrac{3}{8} \qquad \therefore\ \ B(\dfrac{1}{2},\ \dfrac{3}{8})$

$\ell \ の傾き \ \ k=\cfrac{\dfrac{3}{8}}{\dfrac{1}{2}+1}=\cfrac{1}{4}$

$接線 \ \ell \ \ は \quad y=\cfrac{1}{4}(x+1)$


ページの先頭へ↑



メインメニュー　に戻る