神戸大学(理系) 2018年 問題2
$k\ を \ 2\ 以上の整数とする。また、f(x)=\cfrac{1}{k}\big((k-1)x+\cfrac{1}{x^{k-1}}\big)\ \ とおく。以下の問いに答えよ。$
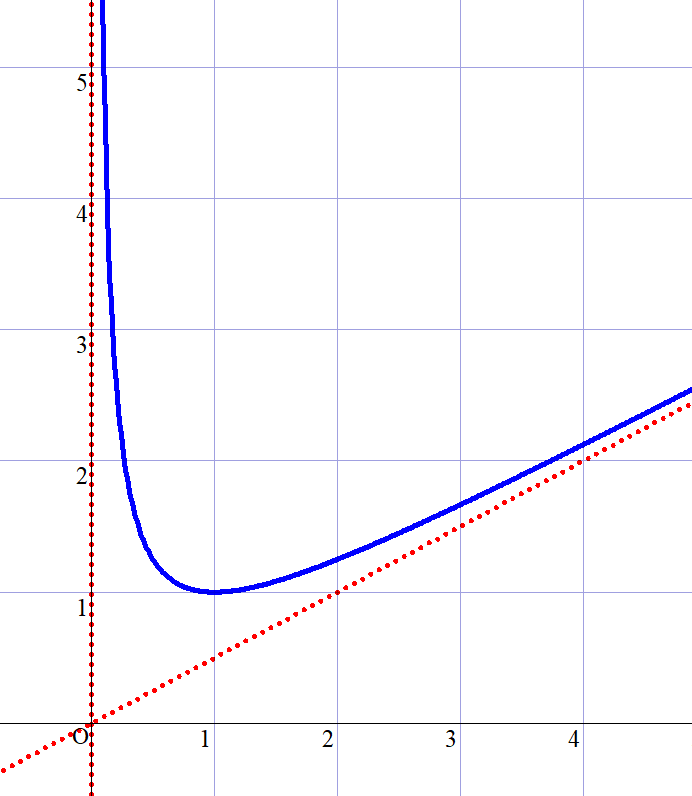
$\qquad (1)\ \ x > 0 \ \ において、関数 \ y=f(x)\ の増減と漸近線を調べてグラフの概形をかけ。$
$\qquad (2)\ \ 数列 \ \{x_n\}\ が \ x_1 > 1 ,\ \ x_{n+1}=f(x_n) \ \ (n=1,\ 2,\ \cdots )\ \ を満たすとき、x_n > 1 \ \ を示せ。$
\[(3)\ \ (2)の数列 \ \{x_n\}\ に対し、x_{n+1}-1 < \cfrac{k-1}{k}(x_n-1)\ \ を示せ。また \ \ \lim _{n \rightarrow \infty}x_n \ \ を求めよ。\]
$(解説)$
$(1)\ \ 漸近線をきちんと求めるのは意外にやっかいです。$
$(2)\ \ グラフをみれば明らかですが、数学的帰納法をつかってきちんと証明しましょう。$
$(3)\ \ この不等式をつかって極限値が求められます。$
(1)
$\quad f'(x)=\cfrac{1}{k}\big(k-1-\cfrac{k-1}{x^k}\big)=\cfrac{k-1}{k}\big(1-\cfrac{1}{x^k}\big)$
$\quad f'(x)=0 \quad より \quad 1-\cfrac{1}{x^k}=0 \qquad x^k=1 \qquad x > 0 \quad だから \quad x=1$
$増減表は$
\[ \begin{array}{c||c|c|c|c|c} \hline x& 0 & \cdots & 1 & \cdots \\ \hline f'(x)& & - & 0 & + & \\ \hline f(x)& & \searrow & 極小 & \nearrow & \\ \hline \end{array} \]
$\quad x=1\ で \ f(x)\ は極小となり、極小値は \quad f(1)=\cfrac{1}{k}(k-1+1)=1$
$\qquad (漸近線については($漸近線$)を参考にしてください。)$
$\quad x \longrightarrow +0 \quad のとき \quad \cfrac{1}{x^{k-1}} \longrightarrow +\infty \quad だから \quad f(x) \longrightarrow +\infty \quad よって \ \ x=0\ は漸近線$
$また、y=mx+n \ \ が漸近線とすると$
\[m=\lim _{x \rightarrow +\infty}\cfrac{f(x)}{x}=\lim _{x \rightarrow +\infty}\big(\cfrac{k-1}{k}+\cfrac{1}{kx^k}\big)=\cfrac{k-1}{k}\]
\[n=\lim _{x \rightarrow +\infty}\big(f(x)-\cfrac{k-1}{k}x\big)=\lim _{x \rightarrow +\infty}\cfrac{1}{kx^{k-1}}=0\]
$よって \quad y=\cfrac{k-1}{k}x \ \ は漸近線である。$
$したがって \ y=f(x)\ の漸近線は \quad x=0 \ \ と \ \ y=\cfrac{k-1}{k}x$
$グラフの概形は右図のとおりです。$
(2)
$数学的帰納法で示します。$
(i)$\ \ 仮定より \quad x_1 > 1 \quad だから \quad n=1\ \ のとき成りたつ。$
(ii)$\ \ n=k \ \ (k \geqq 2)\ \ のとき成りたつとすると \quad x_k > 1$
$\quad (1)より \quad x \ne 1 \quad ならば \quad f(x) > 1 \quad だから$
$\quad x_{k+1}=f(x_k) > 1 \quad よって \quad n=k+1 \quad のときも成りたつ。$
(i),(ii)$\ \ よりすべての自然数について \quad x_n >1 $
(3)
$\quad x_{n+1}-1=f(x_n)-1=\cfrac{1}{k}\big((k-1)x_n+\cfrac{1}{x_n^{k-1}}\big)-1=\cfrac{k-1}{k}x_n+\cfrac{1}{k}\cdot \cfrac{1}{x_n^{k-1}}-1$
$(2)より \quad x_n > 1 \quad だから \quad \cfrac{1}{x_n^{k-1}} <1$
$よって$
$\quad x_{n+1}-1 < \cfrac{k-1}{k}x_n+\cfrac{1}{k}-1=\cfrac{k-1}{k}x_n+\cfrac{1-k}{k}=\cfrac{k-1}{k}(x_n-1)$
$この不等式を繰り返して$
\begin{eqnarray*} x_n-1 &<&\cfrac{k-1}{k}(x_{n-1}-1)\\ &<&\big(\cfrac{k-1}{k}\big)^2(x_{n-2}-1)\\ & & \vdots \\ &<&\big(\cfrac{k-1}{k}\big)^{n-1}(x_1-1)\\ \end{eqnarray*} $\quad 0 < \cfrac{k-1}{k} < 1 \quad だから \quad n \longrightarrow \infty \quad のとき \quad \big(\cfrac{k-1}{k}\big)^{n-1} \longrightarrow 0 \qquad よって \qquad 右辺 \longrightarrow 0$
$\quad また (2)より \quad x_n > 1 \quad だから \quad 左辺 > 0$
\[はさみうちの原理により \quad x_n -1 \longrightarrow 0 \quad となり \quad \lim _{n \rightarrow \infty}x_n =1\]
メインメニュー に戻る