慶応大学(理系) 2025年 問題2
$座標平面上の点P(1,\ 1) と\ Q(1,\ -1)\ および曲線 \ C:y=\dfrac{1}{x-4}\ \ (x > 4)\ \ を考える。$
$(1)\ \ 曲線 \ C\ の接線で点 \ Q\ を通るものは存在しないことを証明しなさい。$
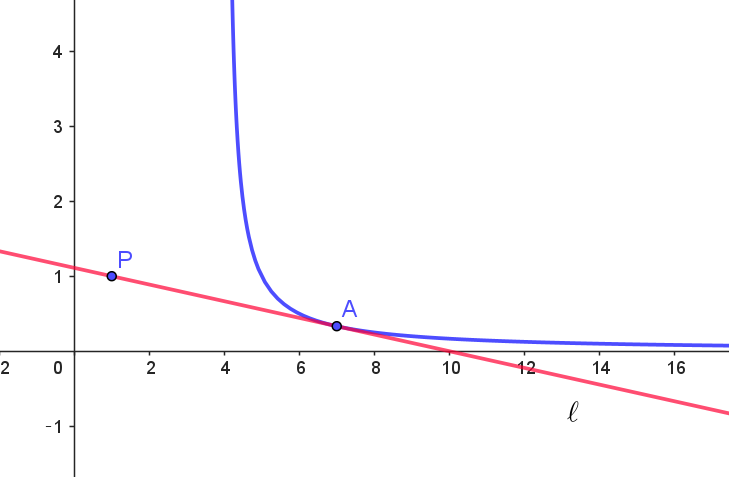
$(2)\ \ 曲線 \ C\ の接線で点 \ P\ を通るものを \ \ell \ とし、C\ と \ \ell \ の接点を \ A\ とする。このとき、\ell \ の方程式は$
$\quad y=\fbox{$\quad (キ) \quad \ $}であり、点 \ A\ の座標は \fbox{$\quad (ク) \quad \ $}である。また、曲線 \ C\ 上の点 \ B\ が$
$\quad \vec{PB}\cdot \vec{PA} + \vec{PA}\cdot \vec{AQ} + \vec{AB}\cdot \vec{AQ}=-\dfrac{2}{3}\ \ を満たすとき、点 \ B\ の座標は\fbox{$\quad (ケ) \quad \ $}である。$
$(3)\ \ A,\ B\ を(2)で定めた点とする。正の数 \ t\ に対し、曲線 \ C\ 上の点 \ R(t+4,\ \dfrac{1}{t})\ は点 \ A\ と異なるものとする。$
$\quad 線分 \ AR\ を \ 2:1\ に内分する点を \ S\ とし、線分 \ BS\ を \ 3:2\ に内分する点を \ T(u,\ v)\ とするとき、u\ を \ t\ の式$
$\quad で表すと \ \ u=\fbox{$\quad (コ) \quad \ $}である。また、uv\ の値は \ t=\fbox{$\quad (サ) \quad \ $}のとき最小となる。$
(1)
$C:y=\dfrac{1}{x-4}\ \ (x > 4)\ \ より \ \ y'=-\cfrac{1}{(x-4)^2}\ \ だから曲線 \ C\ 上の点 \ A(a,\ \dfrac{1}{a-4}) \ \ (a > 4)\ \ における接線は$
$y=-\cfrac{1}{(a-4)^2}(x-a)+ \cfrac{1}{a-4} \hspace{5em}①$
$これが \ Q(1,\ -1)\ を通るとすると$
$-1=-\cfrac{1}{(a-4)^2}(1-a)+ \cfrac{1}{a-4}$
$-(a-4)^2=(a-1)+(a-4)$
$a^2-6a+11=0$
$(a-3)^2+2=0 $
$これを満たす実数 \ a\ は存在しないから\ C\ の接線で点 \ Q\ を通るものは存在しない。$
(2)
$1=-\cfrac{1}{(a-4)^2}(1-a)+ \cfrac{1}{a-4}$
$(a-4)^2=(a-1)+(a-4)$
$a^2-10a+21=0$
$(a-3)(a-7)=0$
$a > 4 \ \ だから \ \ a=7$
$\cfrac{1}{a-4}=\cfrac{1}{7-4}=\cfrac{1}{3} \ \ よって \quad A(7,\ \dfrac{1}{3})$
$このとき、\ell \ の方程式は①より$
$y=-\cfrac{1}{(7-4)^2}(x-7)+ \cfrac{1}{7-4} $
$\ell : y=-\cfrac{1}{9}x+\cfrac{10}{9}$
$B(s,\ t)\ とおくと$
$\vec{PA}=(7,\ \dfrac{1}{3})-(1,\ 1)=(6,\ -\dfrac{2}{3})$
$\vec{AQ}=(1,\ -1)-(7,\ \dfrac{1}{3})=(-6,\ -\dfrac{4}{3})$
$\vec{PB}\cdot \vec{PA} + \vec{PA}\cdot \vec{AQ} + \vec{AB}\cdot \vec{AQ}=-\dfrac{2}{3} \ \ は$
$(s-1,\ t-1)\cdot (6,\ -\dfrac{2}{3})+ (6,\ -\dfrac{2}{3}) \cdot (-6,\ -\dfrac{4}{3})+(s-7,\ t-\dfrac{1}{3}) \cdot (-6,\ -\dfrac{4}{3})=-\cfrac{2}{3}$
$6(s-1)-\dfrac{2}{3}(t-1) + (-36+\dfrac{8}{9}) -6(s-7)-\dfrac{4}{3}(t-\dfrac{1}{3})=-\cfrac{2}{3}$
$2t=\cfrac{8}{3}$
$\therefore \ \ t=\cfrac{4}{3}$
$t=\cfrac{1}{s-4} \ \ に代入して \quad s=\cfrac{1}{t}+4=\cfrac{3}{4}+4=\cfrac{19}{4}$
$よって \quad B(\dfrac{19}{4},\ \dfrac{4}{3})$
(3)
$A(7,\ \dfrac{1}{3}),\quad B(\cfrac{19}{4},\ \cfrac{4}{3}),\quad R(t+4,\ \dfrac{1}{t}) \ \ (t > 0,\ \ t \ne 3)$
$\vec{OS}=\cfrac{1 \times \vec{OA} + 2 \times \vec{OR}}{2+1}=\cfrac{1}{3}(7,\ \dfrac{1}{3})+\cfrac{2}{3}(t+4,\ \dfrac{1}{t})=(\dfrac{2t+15}{3},\ \dfrac{t+6}{9t})$
$\vec{OT}=\cfrac{2 \times \vec{OB} + 3 \times \vec{OS}}{3+2}=\cfrac{2}{5}(\dfrac{19}{4},\ \dfrac{4}{3})+\cfrac{3}{5}(\dfrac{2t+15}{3},\ \dfrac{t+6}{9t})=(\dfrac{4t+49}{10},\ \dfrac{3t+2}{5t})$
$したがって \quad u=\dfrac{4t+49}{10}, \quad v=\dfrac{3t+2}{5t}$
\begin{eqnarray*} uv &=&\dfrac{4t+49}{10} \times \dfrac{3t+2}{5t}\\ \\ &=&\dfrac{12t^2+155t+98}{50t}\\ \\ &=&\dfrac{1}{50}(12t+\dfrac{98}{t})+\cfrac{155}{50}\\ \\ & \geqq& \dfrac{1}{25}\sqrt{12t \times \dfrac{98}{t}} +\cfrac{31}{10} \hspace{5em} (相加相乗平均の不等式より)\\ \\ &=&\dfrac{14\sqrt{6}}{25} +\cfrac{31}{10}\\ \end{eqnarray*} $ただし等号は \quad 12t=\cfrac{98}{t} \ \ のとき、すなわち \quad t^2=\cfrac{98}{12}=\cfrac{49}{6} \ \ のときだから$
$uv \ の値は \ \ t=\cfrac{7}{\sqrt{6}}=\cfrac{7\sqrt{6}}{6} \ \ のとき最小となる。$
メインメニュー に戻る