慶応大学(理系) 2025年　問題1-2


$n\ を自然数とする。1\ から \ n\ までの自然数の中で \ 6\ または \ 8\ または \ 9\ で割り切れるものの個数を \ a_n \ で表す。$
$このとき、a_{30}=\fbox{$\quad (ウ) \quad \ $}\ となる。また、a_n=1000\ を満たす最大の \ n\ は \ \fbox{$\quad (エ) \quad \ $}\ である。$


$1\ から \ n\ までの自然数の中で \ 6,\ 8,\ 9\ で割り切れるものの集合をそれぞれ \ A,\ B,\ C\ とすると$

$A \cap B ,\ \ B \cap C ,\ \ C \cap A \ \ はそれぞれ \ 24,\ 72,\ 18 \ で割り切れるものの集合,$

$A \cap B \cap C \ \ は \ 72\ で割り切れるものの集合である。したがって \ \ B \cap C=A \cap B \cap C$

$集合 \ A\ の要素の個数を \ n(A)\ と表すと \quad n(A)=\big[\dfrac{n}{6}\big] \quad ここに \ [p]\ は実数 \ p\ に対して、p\ を超えない最大の整数で、$

$ガウス記号である。他の集合も同様である。$

$6\ または \ 8\ または \ 9\ で割り切れるものの個数\ a_n \ は \ \ n(A \cup B \cup C)\ \ のことであるから$

\begin{eqnarray*} a_n &=&n(A \cup B \cup C)\\ \\ &=&n(A)+n(B)+n(C)-n(A \cap B)-n(B \cap C)-n(C \cap A)+n(A \cap B \cap C)\\ \\ &=&n(A)+n(B)+n(C)-n(A \cap B)-n(C \cap A)\\ \\ &=&\big[\dfrac{n}{6}\big]+\big[\dfrac{n}{8}\big]+\big[\dfrac{n}{9}\big]-\big[\dfrac{n}{24}\big] -\big[\dfrac{n}{18}\big]\\ \end{eqnarray*} $したがって$

\begin{eqnarray*} a_{30} &=&\big[\dfrac{30}{6}\big]+\big[\dfrac{30}{8}\big]+\big[\dfrac{30}{9}\big]-\big[\dfrac{30}{24}\big] -\big[\dfrac{30}{18}\big]\\ \\ &=&5+3+3-1-1\\ \\ &=&9 \end{eqnarray*}
$\big[\dfrac{n}{6}\big] + \big[\dfrac{n}{8}\big] + \big[\dfrac{n}{9}\big] -\big[\dfrac{n}{24}\big]- \big[\dfrac{n}{18}\big] =A \ \ とおくと \ \ 一般に、 p-1 < [p] \leqq p \quad だから$

$\big(\dfrac{n}{6}-1\big) + \big(\dfrac{n}{8}-1\big) +\big(\dfrac{n}{9}-1\big) - \dfrac{n}{24} - \dfrac{n}{18} < A < \dfrac{n}{6} + \dfrac{n}{8} + \dfrac{n}{9} - \big(\dfrac{n}{24}-1 \big) - \big(\dfrac{n}{18}-1\big) $

$\cfrac{22}{72}n -3 < A < \cfrac{22}{72}n +2$

$\cfrac{11}{36}n -3 < A < \cfrac{11}{36}n +2$

$a_n=A=1000 \ \ を満たす自然数 \ n\ は$

(i)$\ \ \cfrac{11}{36}n -3 < 1000 \ \ より \quad n < \cfrac{1003 \times 36}{11}=3282.5$

(ii)$\ \ 1000 < \cfrac{11}{36}n +2 \ \ より \quad n > \cfrac{998 \times 36}{11}=3266.1$

　

$よって　\quad n=3267,\ 3268,\ \cdots , \ 3282$

$ただし、この \ n\ は \ \ A=1000 \ \ を満たす必要条件で、$

$これらすべての \ n\ が \ a_n=1000 \ を満たすわけではない。$

$最大の \ n\ を求めるには、n=3282\ から順次 \ a_n \ を計算$

$する必要があるが、少ない時間の中で、大変な根気と$

$労力がいる。$

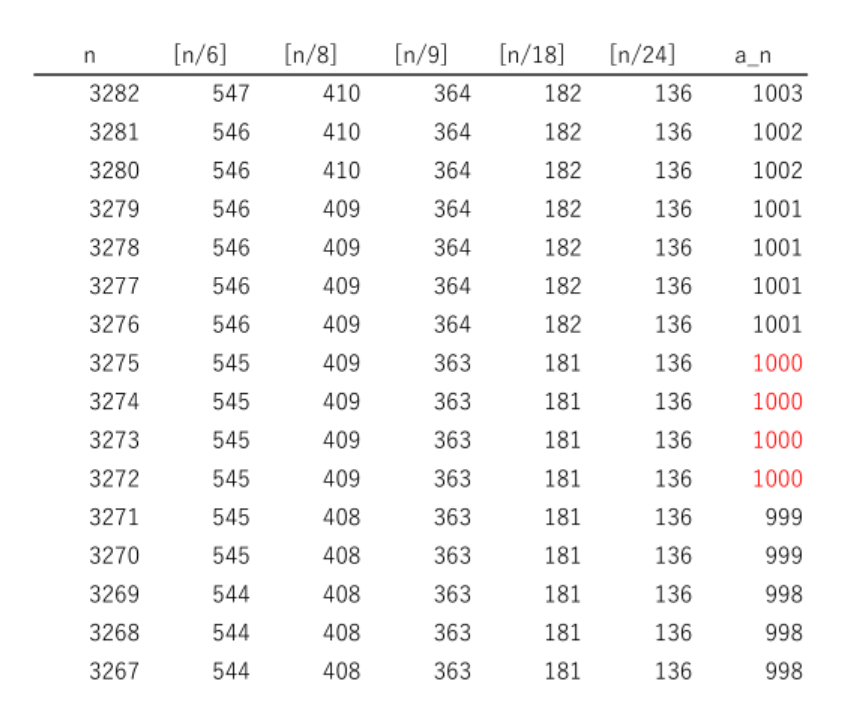
$右の表は \ Excel \ で \ a_n \ を計算したものである。$

$a_n=1000\ を満たす\ n\ は3272,\ 3273,\ 3274,\ 3275\ の \ 4\ 個ある$

$ことがわかる。このうち最大の \ n\ は \ \ 3275 \ \ である。$


$n=3275 \ を決定するもっとうまい解法があると思われるが、とりあえずこれにします。$


ページの先頭へ↑




メインメニュー　に戻る