慶応大学(理系) 2025年　問題1-1


$複素数平面上で、方程式\ |z+i|=2|z-\sqrt{3}|\ を満たす点 \ z\ 全体が表す図形は、中心が\fbox{$\quad (ア) \quad \ $}、半径が$
$\fbox{$\quad (イ) \quad \ $}の円である。$


$z=x+yi \ \ (x,\ y\ は実数) \ \ とおくと$

$|x+(y+1)i|=2|x-\sqrt{3}+yi|$

$x^2+(y+1)^2=4\big\{(x-\sqrt{3})^2+y^2\big\}$

$3x^2+3y^2-8\sqrt{3}x-2y+11=0$

$x^2+y^2-\cfrac{8\sqrt{3}}{3}x-\cfrac{2}{3}y+\cfrac{11}{3}=0$

$\big(x-\cfrac{4\sqrt{3}}{3}\big)^2+\big(y-\cfrac{1}{3}\big)^2=\cfrac{16}{9}$

$したがって\ \ z\ 全体が表す図形は、中心が \ \ \big(\cfrac{4\sqrt{3}}{3} + \cfrac{1}{3}i\big),\ \ 半径が \ \ \cfrac{4}{3}\ \ の円である。$


$(別解)$

$平面上で \ 2\ 定点からの距離の比が一定 \ (1:1\ は除く)\ な点の軌跡は$

$円となり、これを「アポロニウスの円」といいます。$

　

$|z+i|=2|z-\sqrt{3}|\ \ を満たす点 P(z)\ はA(-i),\ B(\sqrt{3})\ \ とおくと$

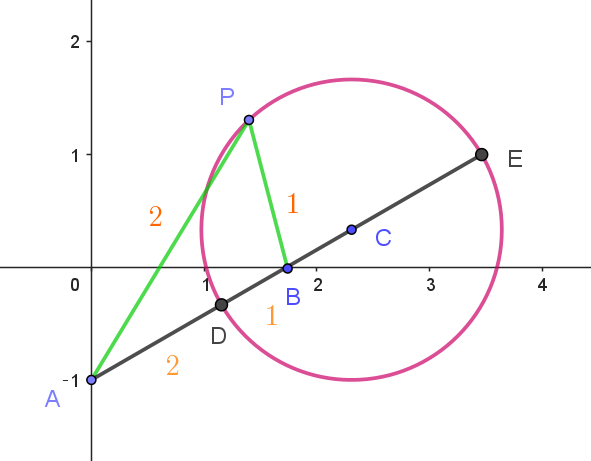
$PA=2PB \ \ すなわち \ \ PA:PB=2:1 \ \ だから円を描く。$

$線分 \ AB\ を \ 2:1 \ に内分する点 \ D\ は \quad \cfrac{1 \times (-i) +2 \times \sqrt{3}}{2+1}=\cfrac{2\sqrt{3}-i}{3}$

$線分 \ AB\ を \ 2:1 \ に外分する点 \ E\ は \quad \cfrac{(-1) \times (-i) +2 \times \sqrt{3}}{2-1}=2\sqrt{3}+i $

$点 \ D,\ E\ は直径の両端だから線分 \ DE\ の中点が円の中心 \ C\ である。$

$\cfrac{\dfrac{2\sqrt{3}-i}{3}+ 2\sqrt{3}+i}{2}=\cfrac{4\sqrt{3}}{3}+ \cfrac{1}{3}i$

$CD=\big(\cfrac{2\sqrt{3}-i}{3}\big)- \big(\cfrac{4\sqrt{3}}{3}+ \cfrac{1}{3}i\big)=-\cfrac{2\sqrt{3}}{3}- \cfrac{2}{3}i$

$半径 \ r\ は \quad r=CD=\sqrt{(-\cfrac{2\sqrt{3}}{3})^2+(- \cfrac{2}{3})^2}=\cfrac{4}{3}$

ページの先頭へ↑




メインメニュー　に戻る