関西学院大学(理系) 2025年 問題3
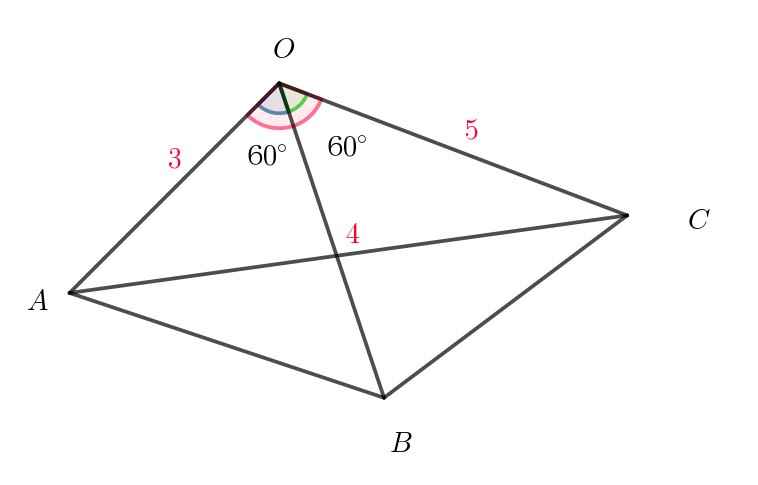
$四面体\ OABC\ は \ OA=3,\ OB=4,\ OC=5,\ \angle AOB=\angle BOC=\angle COA=60 °\ を満たしている。点 \ A\ から$
$平面 \ OBC\ に垂線を引き、平面 \ OBC\ との交点を \ H\ とする。また、\vec{OA}=\vec{a},\ \vec{OB}=\vec{b},\ \vec{OC}=\vec{c}\ とする。$
$(1)\ \ \vec{a} \cdot \vec{b},\ \ \vec{b} \cdot \vec{c},\ \ \vec{c} \cdot \vec{a}\ \ の値をそれぞれ求めよ。$
$(2)\ \ \vec{OH}=p\vec{b}+q\vec{c}\ \ (p,\ q \ は実数)\ \ と表すとき、p,\ q\ の値をそれぞれ求めよ。$
$(3)\ \ 線分 \ OH\ の長さを求めよ。また、\angle BOH=\angle COH \ \ が成り立つことを示せ。$
$(4)\ \ 直線 \ OH \ と辺 \ BC\ の交点を \ M\ とするとき、OH:OM \ \ を求めよ。また、四面体 \ ABCH \ の体積 \ V\ を$
$\quad 求めよ。$
(1)
$\vec{b} \cdot \vec{c}=|\vec{b}||\vec{c}|\cos 60 °=4 \times 5 \times \cos 60°=4 \times 5 \times \dfrac{1}{2}=10$
$\vec{c} \cdot \vec{a}=|\vec{c}||\vec{a}|\cos 60 °=5 \times 3 \times \cos 60°=5 \times 3 \times \dfrac{1}{2}=\cfrac{15}{2}$
(2)
$点\ H\ は平面 \ OBC\ 上にあるから、$
$\vec{OH}=p\vec{b}+q\vec{c} \ \ と表せる。$
$\vec{AH}=\vec{OH}-\vec{OA}=p\vec{b}+q\vec{c}-\vec{a}$
$AH は平面 \ OBC\ に垂直だから$
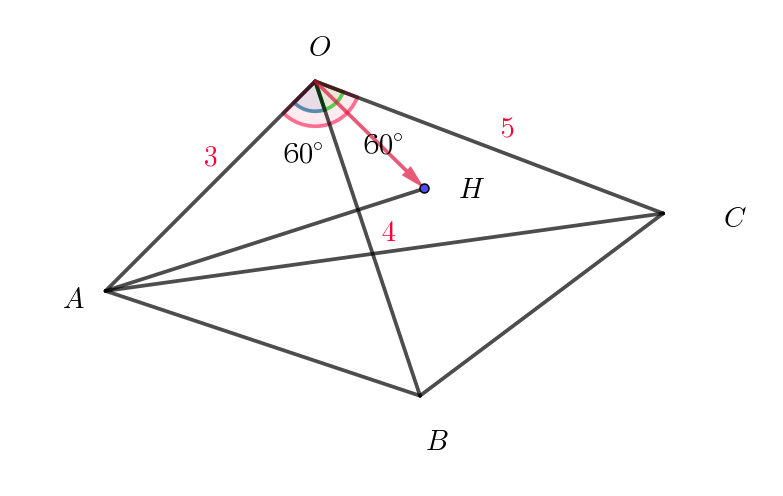
$\quad \vec{AH} \cdot \vec{OB}=0$
$\quad (p\vec{b}+q\vec{c}-\vec{a}) \cdot \vec{b}=0$
$\quad p|\vec{b}|^2 +q\vec{c} \cdot \vec{b}- \vec{a} \cdot \vec{b}=0$
$\quad (1)より \quad 16p+10q-6=0 \hspace{5em}①$
(ii)$\ \ \vec{AH} \perp \vec{OC} \ \ より$
$\quad \vec{AH} \cdot \vec{OC}=0$
$\quad (p\vec{b}+q\vec{c}-\vec{a}) \cdot \vec{c}=0$
$\quad p\vec{b} \cdot \vec{c} +q |\vec{c}|^2 - \vec{a} \cdot \vec{c}=0$
$\quad 10p+25q-\cfrac{15}{2}=0$
$\quad 4p+10q-3=0 \hspace{5em}②$
$①-②より \quad 12p-3=0 \qquad p=\cfrac{1}{4}$
$①に代入して \quad 16 \times \cfrac{1}{4} + 10 q -6=0 \qquad q=\cfrac{1}{5}$
(3)
$(2)より \quad \vec{OH}=\cfrac{1}{4}\vec{b} + \cfrac{1}{5}\vec{c} \quad だから$
\begin{eqnarray*} |\vec{OH}|^2 &=&\big|\cfrac{1}{4}\vec{b} + \cfrac{1}{5}\vec{c}\big|^2\\ \\ &=&\cfrac{1}{16}|\vec{b}|^2 + \cfrac{1}{25}|\vec{c}\big|^2+ \cfrac{1}{10}\vec{b} \cdot \vec{c}\\ \\ &=&\cfrac{1}{16} \times 16 + \cfrac{1}{25} \times 25 + \cfrac{1}{10} \times 10\\ \\ &=&3 \end{eqnarray*} $\therefore \ \ OH=\sqrt{3}$
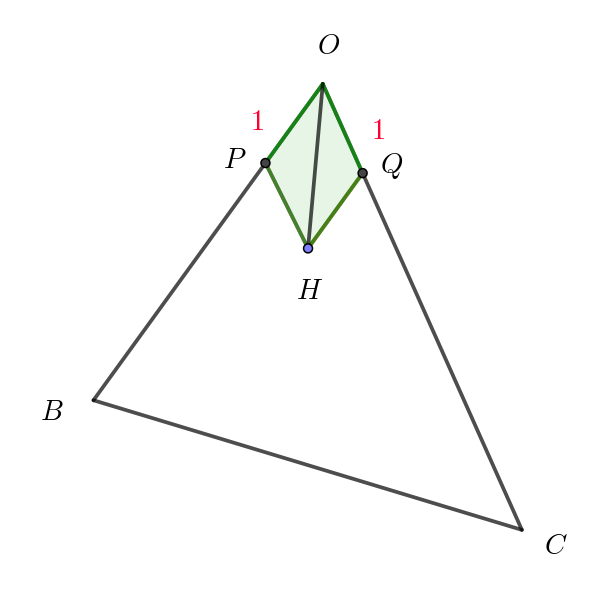
$辺 \ OB上、OC\ 上にとる。$
$\vec{OH}=\cfrac{1}{4}\vec{b} + \cfrac{1}{5}\vec{c} \ \ だから$
$OP=\cfrac{1}{4}OB=\cfrac{1}{4} \times 4=1$
$OQ=\cfrac{1}{5}OQ=\cfrac{1}{5} \times 5=1$
$OP=OQ \ \ だから平行四辺形OPHQ \ はひし形である。$
$したがって \quad \angle POH=\angle QOH \ \ すなわち \ \ \angle BOH=\angle COH $
(4)
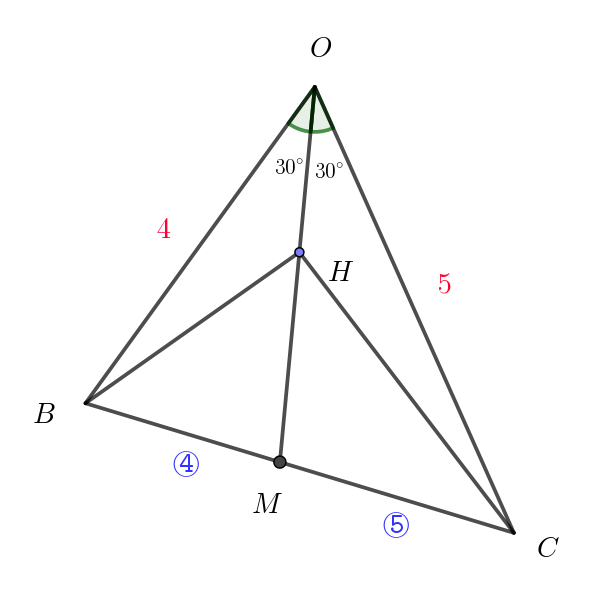
$OB:OC=BM:CM \ \ が成りたち \ \ BM:CM=4:5$
$\quad このことについては($三角形の内角・外角の二等分線の性質$)$
$\quad を参考にしてください。$
$\vec{OM}=\cfrac{5\vec{OB}+4\vec{OC}}{4+5}=\cfrac{1}{9}(5\vec{b}+4\vec{c})$
$一方、3\ 点 \ O,\ H,\ M\ は一直線上にあるから$
$\vec{OM}=k\vec{OH}=k(\cfrac{1}{4}\vec{b} + \cfrac{1}{5}\vec{c})=\cfrac{k}{20}(5\vec{b}+4\vec{c})$
$よって \quad \cfrac{1}{9}=\cfrac{k}{20} \qquad \therefore \ \ k=\cfrac{20}{9}$
$OH:OM=1:k=1:\cfrac{20}{9}=9:20$
$(別解)$
$三角形の内角・外角の二等分線の性質を使わずに、ベクトルのみで求めることもできます。$
$点Mは線分BC上にあるから$
$\vec{OM}=t\vec{OB}+(1-t)\vec{OC}=t\vec{b}+(1-t)\vec{c}\ \ (t\ は実数)\ \ とおける。$
$3\ 点 \ O,\ H,\ M\ は一直線上にあるから$
$\vec{OM}=k\vec{OH}=k(\cfrac{1}{4}\vec{b} + \cfrac{1}{5}\vec{c})=\cfrac{k}{4}\vec{b}+\cfrac{k}{5}\vec{c}$
$よって \quad t\vec{b}+(1-t)\vec{c}=\cfrac{k}{4}\vec{b}+\cfrac{k}{5}\vec{c}$
$\vec{b} \ と \ \vec{c}\ は互いに平行でないから(一次独立)$
\[ \hspace{1em} \left\{ \begin{array}{l} t=\cfrac{k}{4}\\ 1-t=\cfrac{k}{5}\\ \end{array} \right. \]
$これを解いて \quad t=\cfrac{5}{9},\quad k=\cfrac{20}{9}$
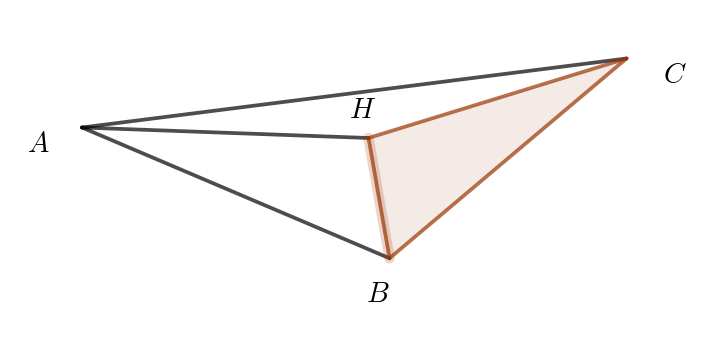
$\triangle HBC \ と \ \triangle OBC \ は底辺 \ BC\ が共通だから面積比は$
$高さの比である。$
$\triangle HBC : \triangle OBC=HM : OM=11:20$
\begin{eqnarray*} \triangle HBC &=&\triangle OBC \times \cfrac{11}{20}\\ \\ &=&\cfrac{1}{2} \times 4 \times 5 \times \sin 60°\times \cfrac{11}{20}\\ \\ &=&\cfrac{11\sqrt{3}}{4} \end{eqnarray*} $AH \perp OH \ \ より \ \ \triangle OAH \ は直角三角形だから$
$AH^2=OA^2-OH^2=3^2-3=6$
$AH \perp \triangle HBC \ \ だから、四面体 \ ABCH \ の体積 \ V\ は$
$V=\cfrac{1}{3} \times \triangle HBC \times AH=\cfrac{1}{3} \times \cfrac{11\sqrt{3}}{4} \times \sqrt{6}=\cfrac{11\sqrt{2}}{4}$
メインメニュー に戻る