関西学院大学(理系) 2025年 問題2
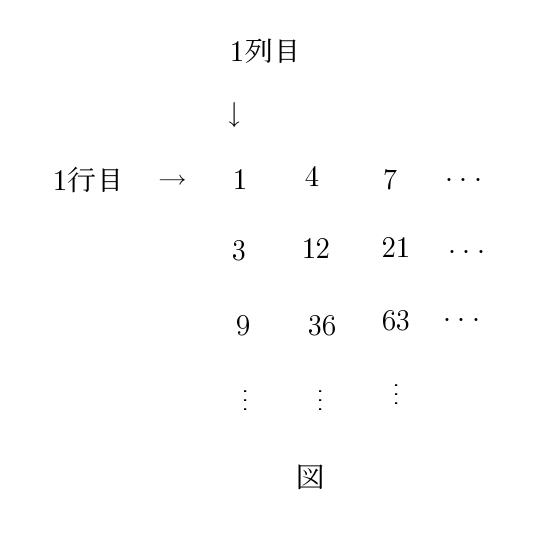
$規則(A)\ \ 1\ 行目は初項 \ 1、公差 \ 3\ の等差数列が、初項から並んでいる。$
$規則(B)\ \ 2\ 行目以降の行は、1\ つ上の行の各数を \ 3\ 倍した数が並んでいる。$
$また、各行に対して、左から順に \ 1\ 列目,\ 2\ 列目,\ \cdots \ とする。例えば、$
$2\ 行目かつ \ 3\ 列目の数は \ 21\ である。\ell,\ m,\ n\ を自然数として、次の \ \fbox{$\quad \quad $}$
$をうめよ。$
$(1)\ \ m\ 行目かつ \ n\ 列目の数を \ m,\ n\ を用いて表すと、\fbox{$\quad ① \quad $}\ である。また、$
$\quad 19521\ は \ \fbox{$\quad ② \quad $}\ 行目かつ \ \fbox{$\quad ③ \quad $}\ 列目の数である。$
$(2)\ \ 1\ 行目の数の中で \ 3^{\ell}\ より小さいものの個数を \ \ell \ を用いて表すと、\fbox{$\quad ④ \quad $}\ である。$
$\quad また、2\ 行目以降も同様に考えて、図に現れる自然数で \ 3^{\ell}\ より小さいものの個数を \ a_{\ell}\ と表す。$
$\quad a_{\ell} \ を \ \ell \ を用いて表すと、a_{\ell}=\fbox{$\quad ⑤ \quad $}\ である。$
$(3)\ \ (2)で求めた \ a_{\ell} \ に対して、\cfrac{1}{a_{\ell} a_{\ell+1}} =\fbox{$\quad ⑥ \quad $} \big(\dfrac{1}{a_{\ell}}-\dfrac{1}{a_{\ell +1}}\big) \ \ が成り立つ。$
\[\quad また、和 \ \ \sum_{k=1}^{\ell} \cfrac{3^k}{a_ka_{k+1}}\ \ を \ \ell \ を用いて表すと、\fbox{$\quad ⑦ \quad $}\ である。\]
(1)
$1\ 行目は初項 \ 1、公差 \ 3\ の等差数列だから第 \ n\ 列目の数は \ \ 1+(n-1) \times 3=3n-2$
$2\ 行目以降の行は、1\ つ上の行の各数を \ 3\ 倍した数が並んでいるから$
$第 \ m\ 行目の数は、第 \ 1\ 行目の数を \ \ 3^{m-1}\ 倍した数が並んでいる。$
$したがって、 m\ 行目かつ \ n\ 列目の数は、(3n-1)3^{m-1}\ \ である。$
$19521 \ を可能な限り \ 3\ で割っていくと \quad 19521=3^4 \times 241=3^4 \times (3 \times 81-2)$
$よって \quad m=5,\quad n=81$
(2)
$(2)\ \ 1\ 行目,第 \ n\ 列の数は \ \ 3n-2 \ \ だから、\ 3^{\ell}\ より小さいものの個数は$
$3n-2 < 3^{\ell} < 3n+1 \ \ を満たす自然数 \ n\ である。$
$両辺を \ 3\ で割って \quad n-\cfrac{2}{3} < 3^{\ell -1} < n +\cfrac{1}{3}$
$3^{\ell -1}\ は自然数だから、区間 \ (n-\dfrac{2}{3} , \ n +\dfrac{1}{3}) \ 内の自然数をさがすと \ n\ だけである。$
$\therefore \ \ n=3^{\ell -1}$
$よって \ \ 3^{\ell}\ \ より小さいものの個数 \ n\ は \quad n=3^{\ell-1}$
$同様にして$
$2\ 行目の数で、\ 3^{\ell}\ より小さいものの個数は \quad 3(3n-2) < 3^{\ell} < 3(3n+1) \ \ を満たす自然数 \ n\ だから $
$n-\cfrac{2}{3} < 3^{\ell -2} < n +\cfrac{1}{3} \qquad \therefore \ \ n=3^{\ell -2}$
$\ell \ 行目の数で、\ 3^{\ell}\ より小さいものの個数は \quad 3^{\ell -1}(3n-2) < 3^{\ell} < 3^{\ell -1}(3n+1) \ \ を満たす自然数 \ n\ だから$
$n-\cfrac{2}{3} < 3^0 < n +\cfrac{1}{3} \qquad \therefore \ \ n=3^0=1$
$図に現れる自然数で \ \ 3^{\ell}\ \ より小さいものの個数 \ a_{\ell}\ \ は$
$a_{\ell}=3^0+3^1+ \cdots + 3^{\ell-1}=\cfrac{3^{\ell}-1}{3-1}=\cfrac{3^{\ell}-1}{2}$
(3)
$\cfrac{1}{a_{\ell} a_{\ell+1}}=\cfrac{2}{3^{\ell}-1} \times \cfrac{2}{3^{\ell +1}-1}=\cfrac{4}{(3^{\ell}-1)(3^{\ell +1}-1)}$
$一方$
\begin{eqnarray*} & &\cfrac{1}{a_{\ell}} - \cfrac{1}{a_{\ell+1}}\\ \\ &=&\cfrac{2}{3^{\ell}-1} - \cfrac{2}{3^{\ell +1}-1}\\ \\ &=&\cfrac{2(3^{\ell +1}-1)-2(3^{\ell}-1)}{(3^{\ell} -1)(3^{\ell +1}-1)}\\ \\ &=&\cfrac{2(3^{\ell +1}-3^{\ell})}{(3^{\ell} -1)(3^{\ell +1}-1)}\\ \\ &=&\cfrac{3^{\ell +1}-3^{\ell}}{2} \times \cfrac{4}{(3^{\ell} -1)(3^{\ell +1}-1)}\\ \\ &=&\cfrac{(3-1)3^{\ell}}{2} \times \cfrac{1}{a_{\ell} a_{\ell+1}}\\ \\ &=&3^{\ell} \times \cfrac{1}{a_{\ell} a_{\ell+1}}\\ \end{eqnarray*} $よって \quad \cfrac{1}{a_{\ell} a_{\ell+1}}=\cfrac{1}{3^{\ell}}\big(\cfrac{1}{a_{\ell}} - \cfrac{1}{a_{\ell+1}}\big)$
$また$
\begin{eqnarray*} & &\sum _{k=1}^{\ell} \cfrac{3^k}{a_ka_{k+1}}\\ \\ & &\sum _{k=1}^{\ell} \big(\cfrac{1}{a_k} - \cfrac{1}{a_{k+1}}\big)\\ \\ &=&\big(\cfrac{1}{a_1} - \cfrac{1}{a_2}\big)+\big(\cfrac{1}{a_2} - \cfrac{1}{a_3}\big)+ \cdots + \big(\cfrac{1}{a_{\ell}} - \cfrac{1}{a_{\ell+1}}\big)\\ \\ &=&\cfrac{1}{a_1} - \cfrac{1}{a_{\ell+1}}\\ \\ &=&1-\cfrac{2}{3^{\ell+1}-1}\\ \\ &=&\cfrac{3^{\ell +1}-3}{3^{\ell +1}-1}\\ \\ &=&\cfrac{3(3^{\ell}-1)}{3^{\ell +1}-1}\\ \end{eqnarray*}
メインメニュー に戻る