関西学院大学(理系) 2025年　問題1


$座標平面上に \ x > 0\ で定義される \ 2\ つの関数 \ f(x)=\dfrac{\log x}{x} ,\ \ g(x)=\dfrac{1}{x}\ \ があり、曲線 \ y=f(x)\ と \ y=g(x)\ を$
$それぞれ \ C_1,\ C_2\ とする。また、C_1\ と \ C_2 \ の共有点の \ x\ 座標を \ \alpha \ とする。ただし、対数は自然対数とする。$
\[以下、必要ならば \ \ \lim _{x \rightarrow \infty} f(x)=0 \ \ を用いてよい。\] $(1)\ \ f(x)\ の増減を調べて、f(x)\ の最大値を求めよ。$
$(2)\ \ \alpha \ の値を求めよ。また、C_1\ と \ C_2\ の概形を解答欄の座標平面上に描け。$
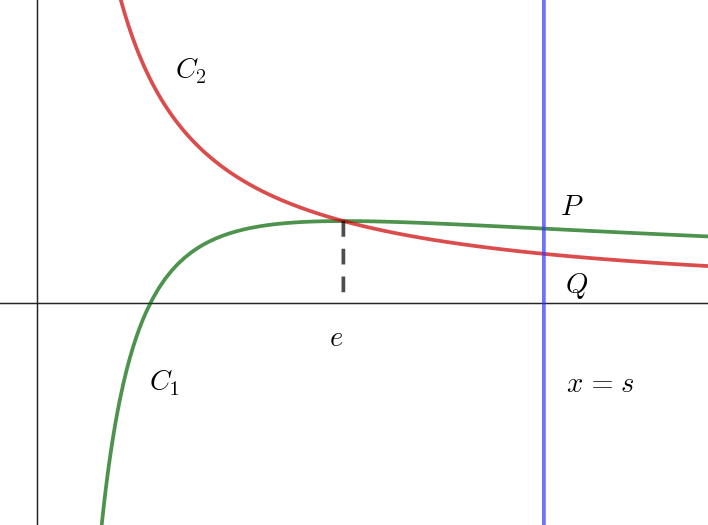
$(3)\ \ s > \alpha \ とし、直線 \ x=s \ と \ C_1,\ C_2\ の交点をそれぞれ \ P,\ Q\ とする。線分 \ PQ\ の長さの最大値とそのとき$
$\quad の \ s\ の値を求めよ。$
$(4)\ \ t > 0 \ とする。C_1,\ C_2\ および直線 \ x=t \ で囲まれる図形の面積が \ 2\ となるような \ t\ の値を求めよ。$


(1)


$f(x)=\dfrac{\log x}{x}\ \ より \ \ f'(x)=\cfrac{\dfrac{1}{x} \times x - \log x}{x^2}=\cfrac{1-\log x}{x^2}$

$f'(x)=0 \ \ より \ \ \log x=1 \qquad x=e$

$増減表$
\[ \begin{array}{c||c|c|c|c|c} x& 0 & \cdots & e & \cdots \\ \hline f'(x)& & + & 0 & - \\ \hline f(x)& & \nearrow & 極大 & \searrow \\ \end{array} \]
$x=e\ で \ f(x)\ は極大かつ最大となり、最大値は \ \ f(e)=\cfrac{1}{e}$


(2)


$x \longrightarrow +0 \ \ のとき \ \ f(x) \longrightarrow -\infty \ \ だから \ y\ 軸は漸近線$

$x \longrightarrow \infty \ \ のとき \ \ f(x) \longrightarrow 0 \ \ だから \ x\ 軸は漸近線$

　

$C_1\ と \ C_2 \ の共有点の \ x\ 座標 \ \alpha \ は$

$\cfrac{\log x}{x}=\cfrac{1}{x} \ \ より \ \ \log x=1 \quad \therefore \ \ x=e$

$よって \quad \alpha =e$

$0 < x < e \ \ のとき \ \ \log x < 1 \ \ より \ \ \cfrac{\log x}{x} < \cfrac{1}{x}$

$ x > e \ \ のとき \ \ \log x > 1 \ \ より \ \ \cfrac{\log x}{x} > \cfrac{1}{x}$

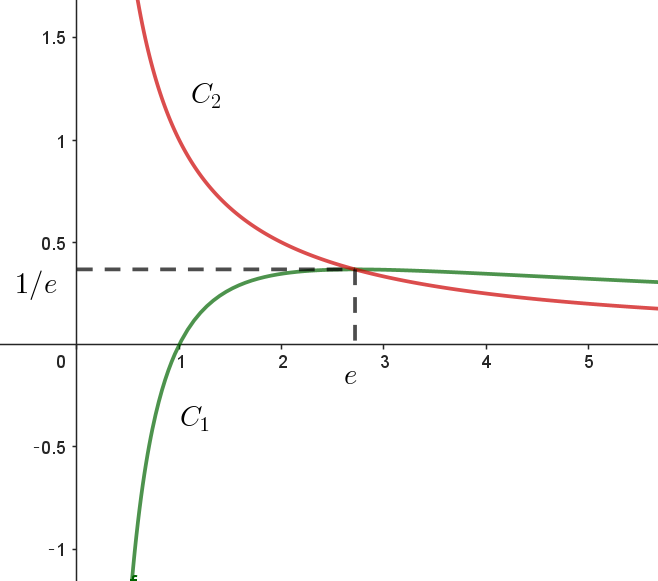
$これらのことから \ C_1\ と \ C_2\ の概形は右図のとおり$


(3)

　

$PQ=f(s)-g(s)=h(s) \quad とおくと$

$h(s)=\cfrac{\log s }{s}-\cfrac{1}{s}=\cfrac{\log s -1}{s}$

$h'(s)=\cfrac{\dfrac{1}{s} \times s -(\log s -1) \times 1}{s^2}=\cfrac{2-\log s}{s^2}$

$h'(s)=0 \ \ より \ \ \log s=2 \qquad s=e^2$

$増減表$
\[ \begin{array}{c||c|c|c|c|c} s& e & \cdots & e^2 & \cdots \\ \hline h'(s)& & + & 0 & - \\ \hline h(s)& & \nearrow & 極大 & \searrow \\ \end{array} \]
$f(e^2)=\cfrac{\log e^2 -1}{e^2}=\cfrac{1}{e^2}$

$線分 \ PQ\ の長さは s= \ \ e^2\ のとき最大値となり、最大値 \ \ \cfrac{1}{e^2}\ \ をもつ$


(4)


$C_1,\ C_2\ および直線 \ x=t \ で囲まれる図形の面積を \ S\ とすると$

　

(i)$\ \ 0 < t < e \ \ のとき$

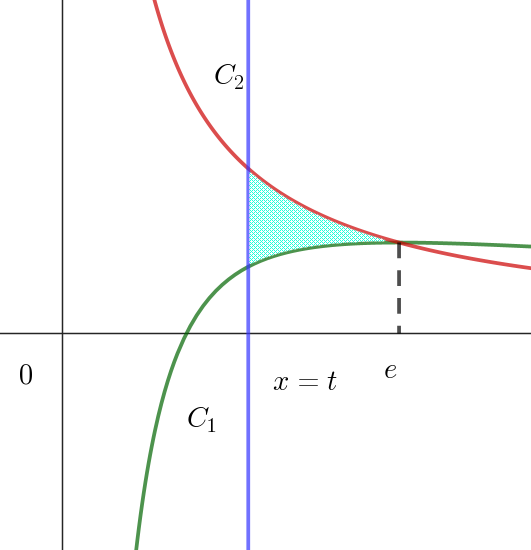
\[S=\int_t^e \big(\dfrac{1}{x}-\dfrac{\log x}{x}\big)dx=\int_t^e \dfrac{1-\log x}{x}dx\]
\[ \log x=u \ \ とおくと \quad \cfrac{dx}{x}=du \qquad \begin{array}{c|c} x & t\ \ \rightarrow \ e \\ \hline u & \ \log t \rightarrow 1 \\ \end{array} \]
\begin{eqnarray*} S &=&\int_{\log t}^1 (1-u)du\\ \\ &=&\big[u-\dfrac{u^2}{2}\big]_{\log t}^1\\ \\ &=&\big(1-\dfrac{1}{2}\big)-\big(\log t - \dfrac{(\log t)^2}{2}\big)\\ \\ &=&\dfrac{(\log t)^2}{2} - \log t +\dfrac{1}{2}\\ \end{eqnarray*} $S=2 \ \ だから$

$\dfrac{(\log t)^2}{2} - \log t +\dfrac{1}{2}=2$

$(\log t)^2 -2 \log t -3=0$

$(\log t +1)(\log t -3)=0$

$\log t=-1 \ \ のとき \ \ t=\cfrac{1}{e}$

$\log t=3 \ \ のとき \ \ t=e^3>e \ \ だから不適$


　

(ii)$\ \ t > e \ \ のとき$

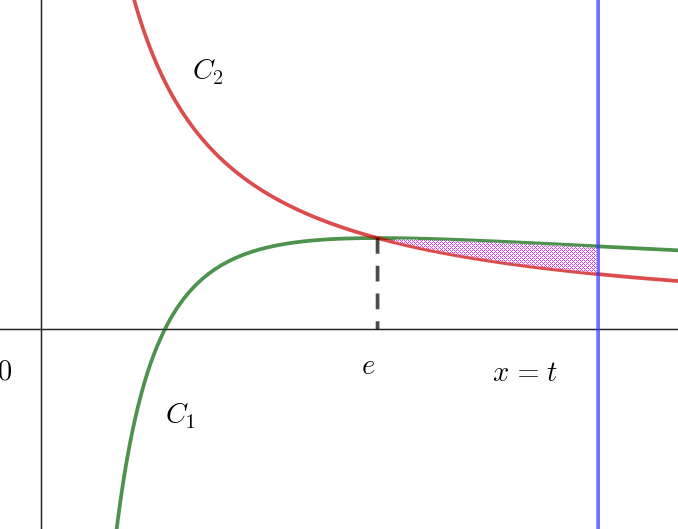
\[S=\int_e^t \big(\dfrac{\log x}{x} - \dfrac{1}{x}\big)dx=-\int_e^t \dfrac{1-\log x}{x}dx=\int_t^e \dfrac{1-\log x}{x}dx\]
(i)$\ \ に帰着するから$

$(\log t +1)(\log t -3)=0$

$\log t=-1 \ \ のとき \ \ t=\cfrac{1}{e} < e \ \ だから不適$

$\log t=3 \ \ のとき \ \ t=e^3$

(i),(ii)$\ \ より \quad t=\cfrac{1}{e},\quad e^3$


$(補充)$

$ x \rightarrow \infty \ \ のとき \ \ \dfrac{\log x}{x} \longrightarrow 0 \ \ については$ 不定形の極限値(1)$をご覧ください。$


ページの先頭へ↑




メインメニュー　に戻る