MY MATH NOTE

金沢大学(理系) 2018年　問題4

$座標空間において、原点 \ (0,\ 0,\ 0)\ と点 \ (1,\ 1,\ -3)\ を通る直線を \ l,\ 2\ つの点 \ (-6,\ 6,\ 0),\ (1,\ 2,\ 1)\ を通る$
$直線を \ m\ とする。直線 \ l\ 上の点 \ P\ と直線 \ m\ 上の点 \ Q\ を、直線 \ PQ\ が直線 \ l,\ m\ のいずれにも直交する$
$ようにとる。次の問いに答えよ。$
$(1)\ \ |\vec{PQ}|\ を求めよ。$
$(2)\ \ A\ を直線 \ l\ 上の点、B\ を直線 \ m\ 上の点とする。ただし、A \ne P\ とする。このとき、\angle APB=\cfrac{\pi}{2}\ で$
$\quad あることを示せ。$
$(3)\ \ 直線 \ l\ 上の2点 \ A,\ C\ をそれらの中点が \ P\ となるようにとる。同様に、直線 \ m\ 上の \ 2\ 点 \ B,\ D\ をそれ$
$\quad らの中点が \ Q\ となるようにとる。|\vec{PA}|=a,\ \ |\vec{QB}|=b\ のとき、三角形 \ BDP\ の面積と四面体 \ ABCD\ の$
$\quad 体積を求めよ。$

(1)

　
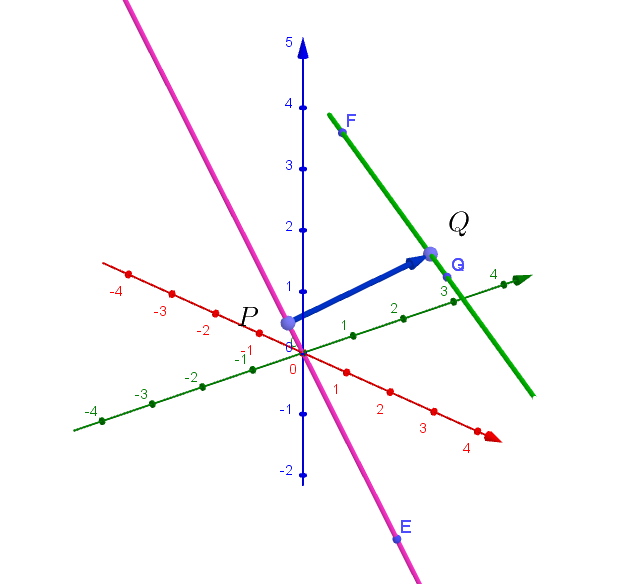
$点 \ E(1,\ 1,\ -3),\ F(-6,\ 6,\ 0),\ G(1,\ 2,\ 1)\ とすると、$
$直線 \ l,\ m\ の方向ベクトルはそれぞれ$
$\quad \vec{d_l}=\vec{OE}=(1,\ 1,\ -3)$
$\quad \vec{d_m}=\vec{FG}=(1,\ 2,\ 1)-(-6,\ 6,\ 0)=(7,\ -4,\ 1)$

$\vec{OP}=t\vec{d_l}=t(1,\ 1,\ -3)=(t,\ t,\ -3t)$
$\vec{OQ}=\vec{OG}+s\vec{d_m}=(1,\ 2,\ 1) + s(7,\ -4,\ 1)=(7s+1,\ -4s+2,\ s+1)$

$よって$
\begin{eqnarray*} \vec{PQ} &=&\vec{OQ}-\vec{OP}\\ &=&(7s+1,\ -4s+2,\ s+1) - (t,\ t,\ -3t)\\ &=&(7s-t+1,\ -4s-t+2,\ s+3t+1)\\ \end{eqnarray*}
(i)$\ \ PQ \perp l \quad より \quad \vec{PQ}\cdot \vec{d_l}=0 $
$\qquad (7s-t+1)\times 1+(-4s-t+2) \times 1+(s+3t+1) \times (-3)=0$
$\qquad \therefore \ \ t=0$

(ii)$\ \ PQ \perp m \quad より \quad 　\vec{PQ}\cdot \vec{d_m}=0 $
$\qquad (7s-t+1)\times 7+(-4s-t+2) \times (-4)+(s+3t+1) \times 1=0$
$\qquad \therefore \ \ s=0$

$したがって \quad \vec{OP}=(0,\ 0,\ 0),\quad \vec{OQ}=(1,\ 2,\ 1)\ となって点 \ P\ は原点、点 \ Q\ は \ G\ に一致する。$

$\vec{PQ}=(1,\ 2,\ 1) \quad より \quad |\vec{PQ}|=\sqrt{1+4+1}=\sqrt{6}$

(2)

　
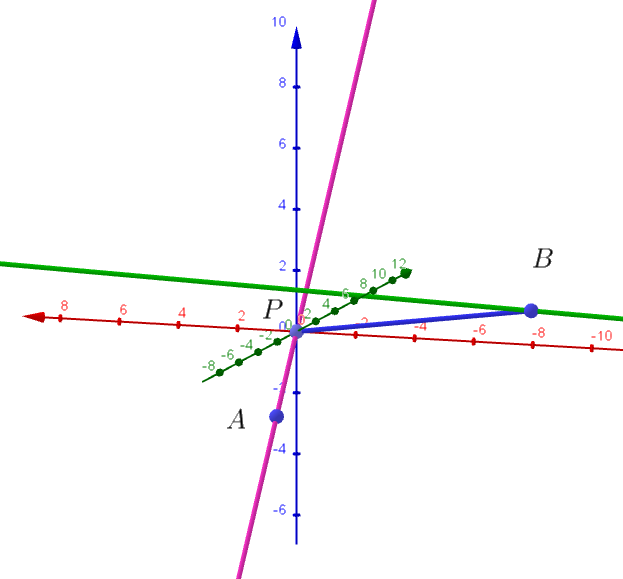
$A(t,\ t,\ -3t),\ B(7s+1,\ -4s+2,\ s+1),\ P(0,\ 0,\ 0)$
$とおけるから$

$\vec{PA}\cdot \vec{PB}=t(7s+1)+t(-4s+2)-3t(s+1)=0$

$よって \quad 　\vec{PA} \perp \vec{PB} \quad となり \quad \angle APB =\cfrac{\pi}{2}$

(3)

　
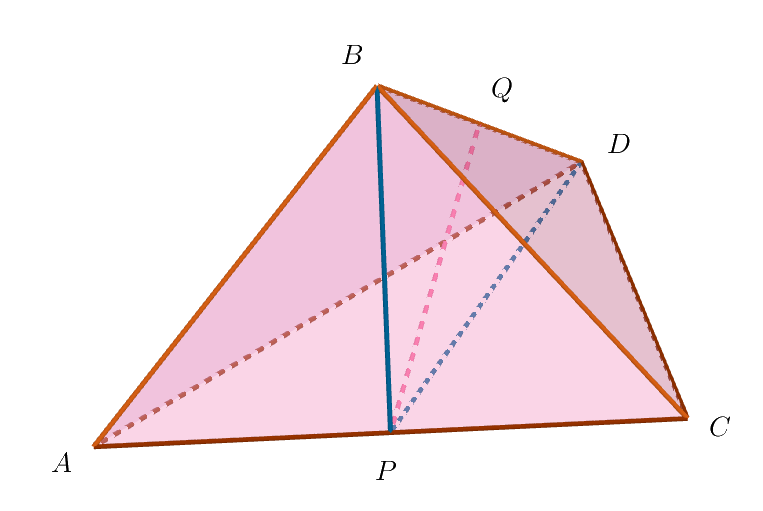
$仮定より、l \perp PQ \quad だから \quad AC \perp PQ $

$(2)より　PA \perp PB \quad だから　AC \perp PB$

$すると \quad AC\ は交わる \ 2\ 直線 \ PQ,\ PB\ に、それぞれ垂直となるから$
$AC\ は \ PQ\ と \ PB\ がつくる平面、すなわち \triangle BDP\ に垂直となる。$
$(このことについては($三垂線の定理$)を参考にしてください。)$

$四面体 \ ABCD \ を \ \triangle BDP \ で分割し、2\ つの四面体をつくる。$

$PC\ は四角錐 \ BDPC\ の高さになり、同様に、PA\ は四角錐 \ BDPA\ の高さになる。$

$よって、四角錐 \ ABCD\ の体積 \ V\ は$
\begin{eqnarray*} V &=&四角錐BDPC+四角錐BDPA\\ \\ &=&\cfrac{1}{3} \times PC \times \triangle BDP + \cfrac{1}{3} \times PA \times \triangle BDP\\ \\ &=&\cfrac{1}{3} \times (PC + PA) \times \triangle BDP \\ \\ &=&\cfrac{1}{3} \times AC \times \triangle BDP\\ \\ &=&\cfrac{1}{3} \times 2a \times \sqrt{6}b\\ \\ &=&\cfrac{2\sqrt{6}}{3}ab\\ \end{eqnarray*}

ページの先頭へ↑