じゃんけんで、ただ1人の勝者が決まるまでの回数の確率
1.2人で行う場合
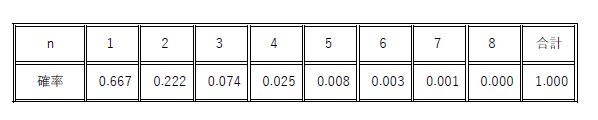
$(1)\ 2回目で勝敗が決まる確率 P(2)$
$\qquad 1回目があいこで、2回目に決まるから$
$\hspace{5em} P(2)=\cfrac{1}{3} \times \cfrac{2}{3}=\cfrac{2}{9}$
$(2)\ n回目で勝敗が決まる確率 p(n)$
$\qquad あいこが連続(n-1)回続き、n回目で勝敗が決まればよいから$
$\hspace{5em} P(n)=(\cfrac{1}{3})^{n-1} \times \cfrac{2}{3}=\cfrac{2}{3^n}$
$\qquad 8回目まで計算したのが下表です。$
$\hspace{2em}$
期待値は
\[E=\sum _{n=1}^\infty nP(n)=\sum _{n=1}^\infty n \times \cfrac{2}{3^n}=2 \sum _{n=1}^\infty \cfrac{n}{3^n}=2 \times \cfrac{3}{4}=\cfrac{3}{2}\hspace{9em}\]
\[\sum _{n=1}^\infty \cfrac{n}{3^n}=\cfrac{3}{4} になることは次を参照してください。\hspace{10em}\] $\hspace{20em}$($\sum_{n=1}^\infty n^ka^n の漸化式)$
2.3人で行う場合
$(1)\ 2回目で勝敗が決まる確率 P(2)$
$\quad $(i)$\ 1回目があいこで、2回目に3人のうち1人が勝つ場合$
$\hspace{5em} \cfrac{1}{3} \times \cfrac{1}{3}=\cfrac{1}{9}$
$\quad $(ii)$\ 1回目に2人勝ち、2回目に2人のうち1人が勝つ場合$
$\hspace{5em} \cfrac{1}{3} \times \cfrac{2}{3}=\cfrac{2}{9}$
よって
$\hspace{5em} P(2)=\cfrac{1}{9}+\cfrac{2}{9}=\cfrac{1}{3}$
$(2)\ 3回目で勝敗が決まる確率 P(3)$
$\quad $(i)$\ 1回目、2回目があいこで、3回目に3人のうち1人が勝つ場合$
$\hspace{5em} \cfrac{1}{3} \times \cfrac{1}{3} \times \cfrac{1}{3}=\cfrac{1}{27}$
$\quad $(ii)$\ 1回目があいこで、2回目に2人が勝ち、3回目に2人のうち1人が勝つ場合$
$\hspace{5em} \cfrac{1}{3} \times \cfrac{1}{3} \times \cfrac{2}{3}=\cfrac{2}{27}$
$\quad $(iii)$\ 1回目に2人が勝ち、2回目に2人があいこ、3回目に2人のうち1人が勝つ場合$
$\hspace{5em} \cfrac{1}{3} \times \cfrac{1}{3} \times \cfrac{2}{3}=\cfrac{2}{27}$
よって
$\hspace{5em} P(3)=\cfrac{1}{27}+\cfrac{2}{27}+\cfrac{2}{27}=\cfrac{5}{27}$
$(3)\ n回目で勝敗が決まる確率 P(n)$
$\quad $(i)$\ 1回目、……、(n-1)回目があいこで、n回目にn人のうち1人が勝つ場合$
$\hspace{5em} (\cfrac{1}{3})^{n-1} \times \cfrac{1}{3}$
$\quad $(ii)$\ r回までは3人のあいこ、次に3人のうち2人が勝ち、続いて(n-1)回目までは2人のあいこ、$
$\qquad n回目に2人のうち1人が勝つ場合$
$\qquad $3人のあいこを ◎ 、3人のうち2人が勝つを△、2人のあいこを ○ 、2人のうち1人が勝つを
$\qquad □とすると$
$\hspace{5em}$ ◎◎……◎△○○……○|□ となるが
$\qquad $ ◎と○の確率はともに $\cfrac{1}{3}$ で等しいので、◎を○とおきかえて
$\hspace{5em}$ ○○……○△○○……○|□ と考えると
$\qquad (n-1)回までは、(n-2)個の$ ○ と、1個の△$の同じものを含む順列となって$
$\hspace{5em} \cfrac{(n-1)!}{(n-2)!}=n-1 通りあるから (n-1) \times (\cfrac{1}{3})^{n-1} \times \cfrac{2}{3}$
よって
$\hspace{5em} P(n)=(\cfrac{1}{3})^{n-1} \times \cfrac{1}{3} + (n-1) \times (\cfrac{1}{3})^{n-1} \times \cfrac{2}{3}=\cfrac{2n-1}{3^n}$
$10$回目までの確率を計算したのが下表です。

期待値は
\[E=\sum _{n=1}^\infty n \times \cfrac{2n-1}{3^n}=2 \sum _{n=1}^\infty \cfrac{n^2}{3^n}- \sum _{n=1}^\infty \cfrac{n}{3^n} =2 \times \cfrac{3}{2}-\cfrac{3}{4}=\cfrac{9}{4}\hspace{10em}\]
\[ここで、\sum _{n=1}^\infty \cfrac{n^2}{3^n}=\cfrac{3}{2} になることは別項目で説明します。\hspace{12em} \] $\hspace{16em}$ (参照 $\sum_{n=1}^\infty n^ka^n の漸化式)$
3.4人で行う場合
$(1)\ 2回目で勝敗が決まる確率 P(2)$
$\quad $(i)$\ 1回目があいこで、2回目に4人のうち1人が勝つ場合$
$\hspace{5em} \cfrac{13}{27} \times \cfrac{_4C_1 \times 3}{3^4}=\cfrac{13}{27} \times \cfrac{4}{27}$
$\quad $(ii)$\ 1回目に3人勝ち、2回目に3人のうち1人が勝つ場合$
$\hspace{5em} \cfrac{_4C_3 \times 3}{3^4} \times \cfrac{_3C_1 \times 3}{3^3}=\cfrac{4}{27} \times \cfrac{1}{3}$
$\quad $(iii)$\ 1回目に2人勝ち、2回目に2人のうち1人が勝つ場合$
$\hspace{5em} \cfrac{_4C_2 \times 3}{3^4} \times \cfrac{_2C_1 \times 3}{3^2}=\cfrac{2}{9} \times \cfrac{2}{3}$
よって
$\hspace{5em} P(2)=\cfrac{13}{27} \times \cfrac{4}{27}+\cfrac{4}{27} \times \cfrac{1}{3}+\cfrac{2}{9} \times \cfrac{2}{3}=\cfrac{196}{729}$
$(2)\ 3回目で勝敗が決まる確率 P(3)$
$\quad $(i)$\ 1回目、2回目があいこで、3回目に4人のうち1人が勝つ場合$
$\hspace{5em} \cfrac{13}{27} \times \cfrac{13}{27} \times \cfrac{4}{27}=\cfrac{13^2 \times 4}{27^3}$
$\quad $(ii)$\ 1回目が4人のあいこで、2回目に4人のうち3人が勝ち、3回目に3人のうち1人が勝つ場合$
$\hspace{5em} \cfrac{13}{27} \times \cfrac{4}{27} \times \cfrac{1}{3}=\cfrac{13 \times 4}{27^2 \times 3}$
$\quad $(iii)$\ 1回目に4人のうち3人が勝ち、2回目が3人のあいこで、3回目に3人のうち1人が勝つ場合$
$\hspace{5em} \cfrac{4}{27} \times \cfrac{1}{3} \times \cfrac{1}{3}=\cfrac{4}{27 \times 3^2}$
$\quad $(iv)$\ 1回目が4人のあいこで、2回目に4人のうち2人が勝ち、3回目に2人のうち1人が勝つ場合$
$\hspace{5em} \cfrac{13}{27} \times \cfrac{2}{9} \times \cfrac{2}{3}=\cfrac{13 \times 2^2}{27^2}$
$\quad $(v)$\ 1回目が4人のうち2人が勝ち、2回目が2人のあいこで、3回目に2人のうち1人が勝つ場合$
$\hspace{5em} \cfrac{2}{9} \times \cfrac{1}{3} \times \cfrac{2}{3}=\cfrac{2^2}{3^4}$
$\quad $(vi)$\ 1回目に4人のうち3人が勝ち、2回目に3人のうち2人が勝ち、3回目に2人のうち1人が$
勝つ場合
$\hspace{5em} \cfrac{4}{27} \times \cfrac{1}{3} \times \cfrac{2}{3}=\cfrac{8}{27 \times 3^2}$
よって
$\hspace{5em} P(3)=\cfrac{4}{27^3} \times (13^2+13 \times 9+81+13 \times 27+9^2 \times 3+6 \times 27)=\cfrac{4 \times 1123}{27^3}$
このように、あいこの確率が変化する場合は確率の計算は格段にやっかいになります。
そこで、計算で求めることはあきらめて、Excel VBA でモンテカルロ法によるシミュレーションを
行いました。その結果が下表です。
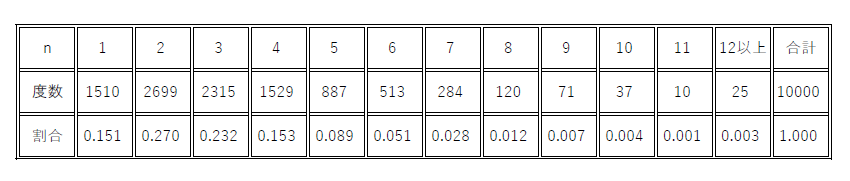
$\hspace{6em}$
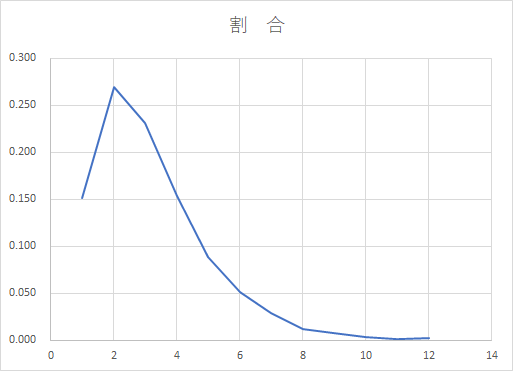
$\hspace{6em}期待値は E= 3.18$
4.5人で行う場合
シミュレーションの結果は下表です。
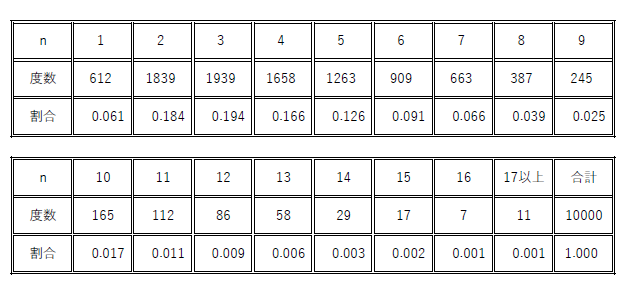
$\hspace{6em}$
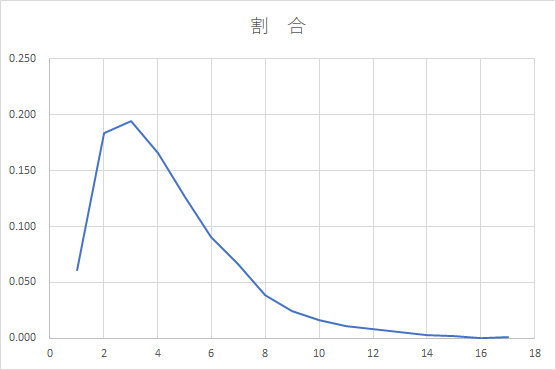
$\hspace{6em}期待値は E=4.41 $
5.$k$人の場合
$(1)\ 2回目で勝敗が決まる確率 P(2)のみ計算します。$
$\quad $(i)$\ 1回目があいこで、2回目にk人のうち1人が勝つ場合$
$\hspace{5em} \cfrac{3^{k-1}-2^k+2}{3^{k-1}} \times \cfrac{_kC_1}{3^{k-1}}$
$\quad $(ii)$\ 1回目に2人勝ち、2回目に2人のうち1人が勝つ場合$
$\hspace{5em} \cfrac{_kC_2}{3^{k-1}} \times \cfrac{2}{3}$
$\quad $(iii)$\ 1回目に3人勝ち、2回目に3人のうち1人が勝つ場合$
$\hspace{5em} \cfrac{_kC_3}{3^{k-1}} \times \cfrac{1}{3}$
$\quad $(iv)$\ 1回目にr人勝ち、2回目にr人のうち1人が勝つ場合$
$\hspace{5em} \cfrac{_kC_r}{3^{k-1}} \times \cfrac{_rC_1}{3^{r-1}}$
よって
\begin{eqnarray*} P(2)&=&\cfrac{3^{k-1}-2^k+2}{3^{k-1}} \times \cfrac{_kC_1}{3^{k-1}}+ \sum_{r=2}^{k-1} \cfrac{_kC_r}{3^{k-1}} \times \cfrac{_rC_1}{3^{r-1}} \hspace{22em}\\ &=&\cfrac{3^{k-1}-2^k+2}{3^{k-1}} \times \cfrac{_kC_1}{3^{k-1}}+ \sum_{r=2}^{k-1} \cfrac{r _kC_r}{3^{k+r-2}}\\ \end{eqnarray*}
じゃんけん に戻る
メインメニュー に戻る