n人で1回じゃんけんをする
1。r人が勝つ確率
2。「あいこ」となる確率
2人が1回だけじゃんけんをするとき
(1) 1人が勝ち、1人が負ける確率 $P_1$
2人のすべての手の出し方は $3^2$通り
勝つ1人の選び方は $_2C_1$ 通り
勝つ手の出し方は、グー、チョキ、パーの3通り
よって
$\hspace{2em} P_1=\cfrac{_2C_1 \times 3}{3^2}=\cfrac{2}{3}$
(2) あいことなる確率 $P_0$
全事象は、あいこ(0人勝つ)になる場合と1人勝つ場合だから
$\hspace{2em} P_0+P_1=1$ より
$\hspace{2em} P_0=1-P_1=1-\cfrac{2}{3}=\cfrac{1}{3}$
$\hspace{3em}$
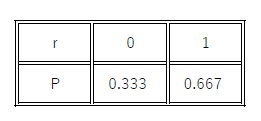
期待値は $E=0 \times \cfrac{1}{3}+1 \times \cfrac{2}{3}=\cfrac{2}{3}=0.667$
3人が1回だけじゃんけんをするとき
(1) 1人が勝ち、2人が負ける確率 $P_1$
3人のすべての手の出し方は $3^3$通り
勝つ1人の選び方は $_3C_1$ 通り
勝つ手の出し方は、グー、チョキ、パーの3通り
よって
$\hspace{2em} P_1=\cfrac{_3C_1 \times 3}{3^3}=\cfrac{1}{3}$
(2) 2人が勝ち、1人が負ける確率 $P_2$
勝つ2人の選び方は $_3C_2$ 通り
勝つ手の出し方は 3通り
よって
$\hspace{2em} P_2=\cfrac{_3C_2 \times 3}{3^3}=\cfrac{1}{3}$
(3) あいことなる確率 $P_0$
全事象は、あいこ(0人勝つ)、1人勝つ、2人勝つ場合だから
$\hspace{2em} P_0+P_1+P_2=1$ より
$\hspace{2em} P_0=1-P_1-P_2=1-\cfrac{1}{3}-\cfrac{1}{3}=\cfrac{1}{3}$
$\hspace{3em}$
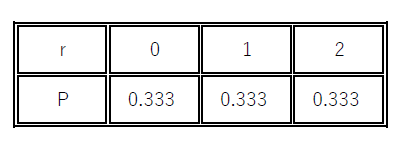
期待値は $E=0 \times \cfrac{1}{3}+1 \times \cfrac{1}{3}+2 \times \cfrac{1}{3}=1$
4人が1回だけじゃんけんをするとき
(1) 1人が勝ち、3人が負ける確率 $P_1$
4人のすべての手の出し方は $3^4$通り
勝つ1人の選び方は $_4C_1$ 通り
勝つ手の出し方は、グー、チョキ、パーの3通り
よって
$P_1=\cfrac{_4C_1 \times 3}{3^4}=\cfrac{4}{27}$
(2) 2人が勝ち、2人が負ける確率 $P_2$
勝つ2人の選び方は $_4C_2$ 通り
よって
$\hspace{2em} P_2=\cfrac{_4C_2 \times 3}{3^4}=\cfrac{2}{9}$
(3) 3人が勝ち、1人が負ける確率 $P_3$
勝つ3人の選び方は $_4C_3$ 通り
よって
$\hspace{2em} P_3=\cfrac{_4C_3 \times 3}{3^4}=\cfrac{4}{27}$
(4) あいことなる確率 $P_0$
全事象は、あいこ(0人勝つ)、1人勝つ、2人勝つ、3人勝つの場合だから
$\hspace{2em} P_0+P_1+P_2+P_3=1$ より
$\hspace{2em} P_0=1-P_1-P_2-P_3=1-\cfrac{4}{27}-\cfrac{2}{9}-\cfrac{4}{27}=\cfrac{13}{27}$
$\hspace{3em}$
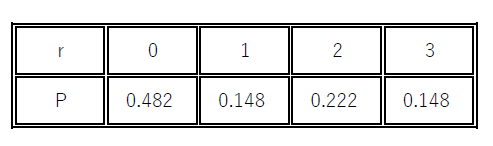
期待値は $E=0 \times \cfrac{13}{27}+1 \times \cfrac{4}{27}+2 \times \cfrac{2}{9}+3 \times \cfrac{4}{27}=\cfrac{28}{27}=1.037$
n人が1回だけじゃんけんをするとき
(1) 1人が勝ち、(n-1)人が負ける確率 $P_1$
n人のすべての手の出し方は $3^n$通り
勝つ1人の選び方は $_nC_1$ 通り
勝つ手の出し方は、グー、チョキ、パーの 3通り
よって
$P_1=\cfrac{_nC_1 \times 3}{3^n}=\cfrac{_nC_1}{3^{n-1}}$
(2) r人が勝ち、(n-r)人が負ける確率 $P_r$
勝つr人の選び方は $_nC_r$ 通り
よって
$P_r=\cfrac{_nC_r \times 3}{3^n}=\cfrac{_nC_r}{3^{n-1}}$
(3) あいことなる確率 $P_0$
全事象は、あいこ(0人勝つ)、1人勝つ、……、(n-1)人勝つ場合だから
$\hspace{2em} P_0+P_1+P_2+\cdots +P_{n-1}=1$ より
\begin{eqnarray*} P_0 &=&1-(P_1+P_2+\cdots +P_{n-1}) \hspace{30em}\\ &=&1-\sum_{r=1}^{n-1}P_r\\ &=&1-\sum_{r=1}^{n-1}\cfrac{_nC_r}{3^{n-1}}\\ &=&1-\cfrac{1}{3^{n-1}}\sum_{r=1}^{n-1}{_nC_r}\\ \end{eqnarray*} 二項定理
\[(a+b)^n=a^n+_nC_1a^{n-1}b+_nC_2a^{n-2}b^2+\cdots +_nC_{n-1}ab^{n-1}+b^n\hspace{15em}\] で、$a=b=1$ とおくと
\begin{eqnarray*} 2^n &=&1+_nC_1+_nC_2+\cdots +_nC_{n-1}+1 \hspace{23em}\\ &=&2+\sum_{r=1}^{n-1}{_nC_r}\\ \end{eqnarray*} \[\therefore \quad \sum_{r=1}^{n-1}{_nC_r}=2^n-2 \hspace{35em}\] $よって$
$\hspace{4em} P_0=1-\cfrac{2^n-2}{3^{n-1}}=\cfrac{3^{n-1}-2^n+2}{3^{n-1}}$
これらををつかうと簡単に計算できます。
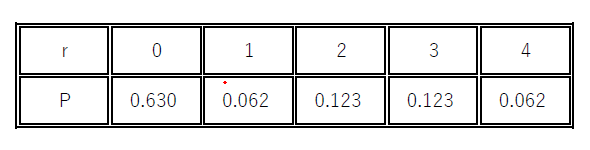
$\hspace{2em}$
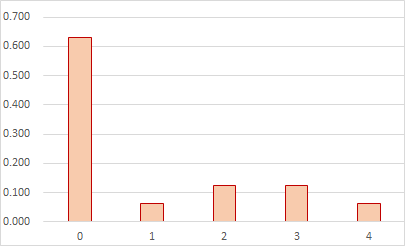
期待値は $E=0 \times \cfrac{17}{27}+1 \times \cfrac{5}{81}+2 \times \cfrac{10}{81}+3 \times \cfrac{10}{81}+4 \times \cfrac{5}{81}=\cfrac{75}{81}=0.926$
$\hspace{2em}$
$\hspace{2em}$
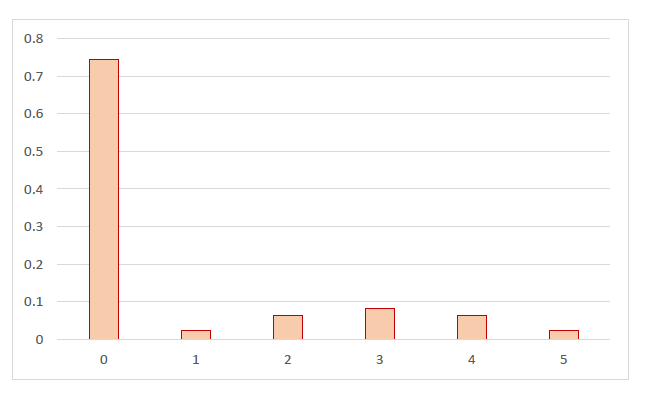
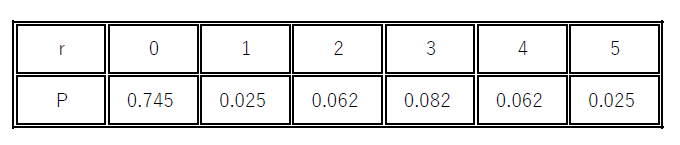
期待値は
$\hspace{1em} E=0 \times \cfrac{181}{3^5}+1 \times \cfrac{6}{3^5}+2 \times \cfrac{15}{3^5}+3 \times \cfrac{20}{3^5}+4 \times \cfrac{15}{3^4}+5 \times \cfrac{6}{3^5}=\cfrac{186}{3^5} =0.765$
このように$n$が大きくなるにつれて、あいこの確率が高くなり、勝つ人数の期待値(平均値)が
小さくなるが、経験的にも納得がいくものです。
これをもっとわかりやすくしたものが次の説明です。
n人が1回だけじゃんけんをするときのあいこになる確率

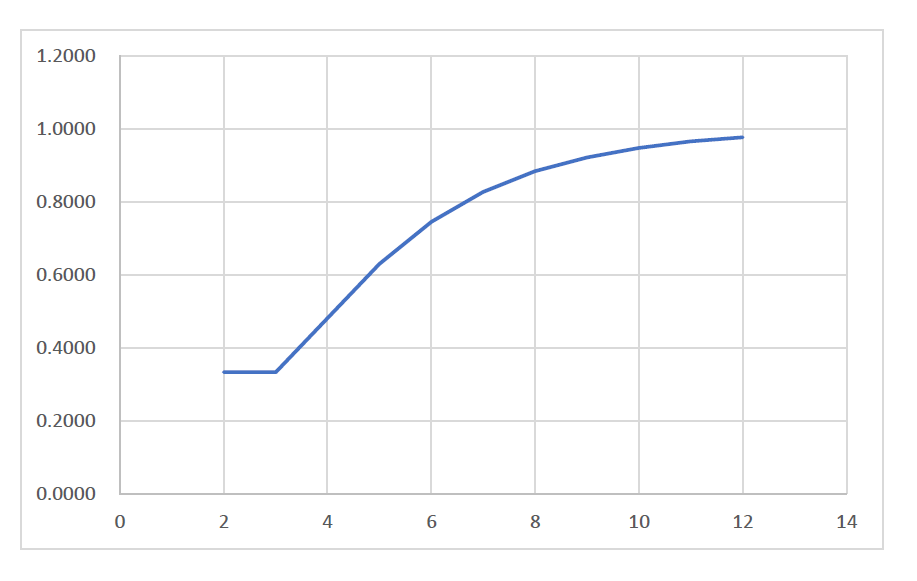
この表やグラフからわかるように、人数が多くなれば、あいこになる確率が高くなります。
例えば、10人では何と95%の割合であいこになってしまいます。
したがって、逆に勝つ人の割合は0に近づくことになります。
じゃんけん に戻る
メインメニュー に戻る