一筆書き
$第二次世界大戦まではドイツ領であった東プロシャに$
$ケーニヒスベルグという街がありました。$
$(現在はロシアでカリーニングラードという名になっているそうです。)$
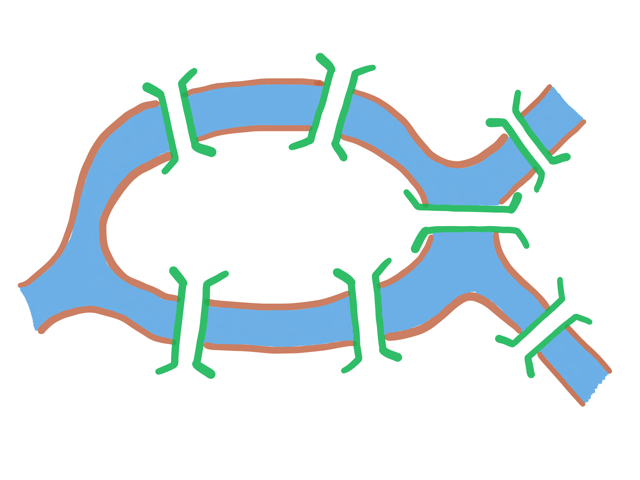
$この街には、2つの川にはさまれた島になっている部分がああり、$
$右図のように7つの橋がかかっていました。$
$ここで、ある人が「同じ橋を二度は通らないようにして、$
$この7つの橋を全部渡ることができるか」という問題を出しました。$
$これは「ケーニヒスベルグの橋」の問題といわれ、多くの人が挑戦$
$しましたが解答が得られませんでした。$
$そのうち、この問題を聞いたスイスの数学者レオンハルト・オイラー(1707~1783)はたちまちのうちに$
$「7つの橋をすべて渡ることは不可能である」ことを証明したのでした。$
$オイラーはどのようにしてこの問題を解いたのでしょうか。$
$2 \ \ 一筆書き$
$一度、書き始めたらペン先を紙から離さずに最後まで書く図形を一筆書きといいます。$
$ただし、一度通った線とは交わってもよいが、同じ線を2度通ってはいけません。$
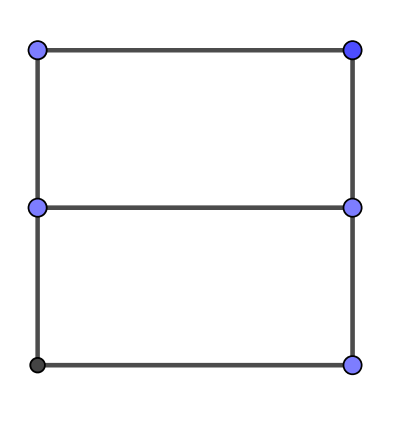
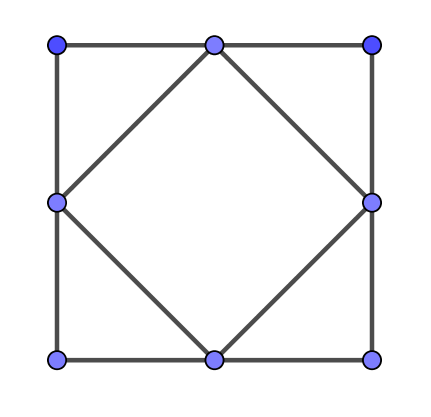
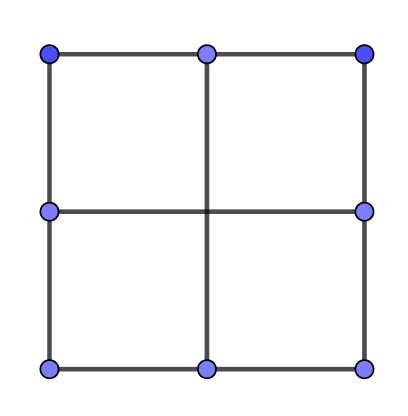
$問題 \ \ 次の図形は一筆書きで書けますか。書けるときは、書き始めと書き終わりの点に印をつけて$
$\hspace{3em} 書き方がわかるようにしておきましょう。$
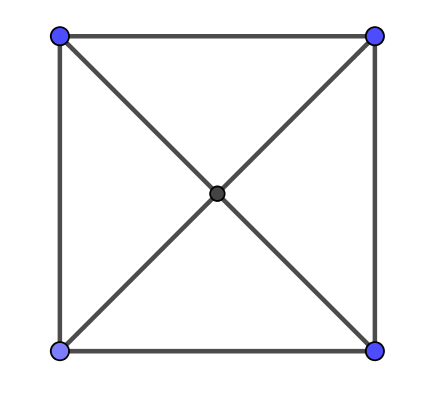
$3 \ \ 奇数点と偶数点$
$図形の頂点や交点から出ている線の本数が奇数のときこの点を奇数点、偶数のとき偶数点といいます。$


$問題の図形について、奇数点と偶数点の個数を調べてみましょう。$

$このように、図形には一筆書きで書けるものと、どんなに工夫$
$しても絶対に書けないものがあります。$
$それでは、一筆書きが可能な条件とは何でしょうか。$
$一筆書き可能な条件$
$\hspace{1em}(1)\ \ 頂点がすべて偶数点であるとき$
$\hspace{3em}このときは、どの頂点から出発してもよい。最後はまた出発点にもどる。$
$\hspace{1em}(2)\ \ 奇数点が2個で、他の頂点はすべて偶数点であるとき$
$\hspace{3em}奇数点の一方が出発点で、他方が終点となる。$
$4\ \ ケーニヒスベルグの橋(2)$
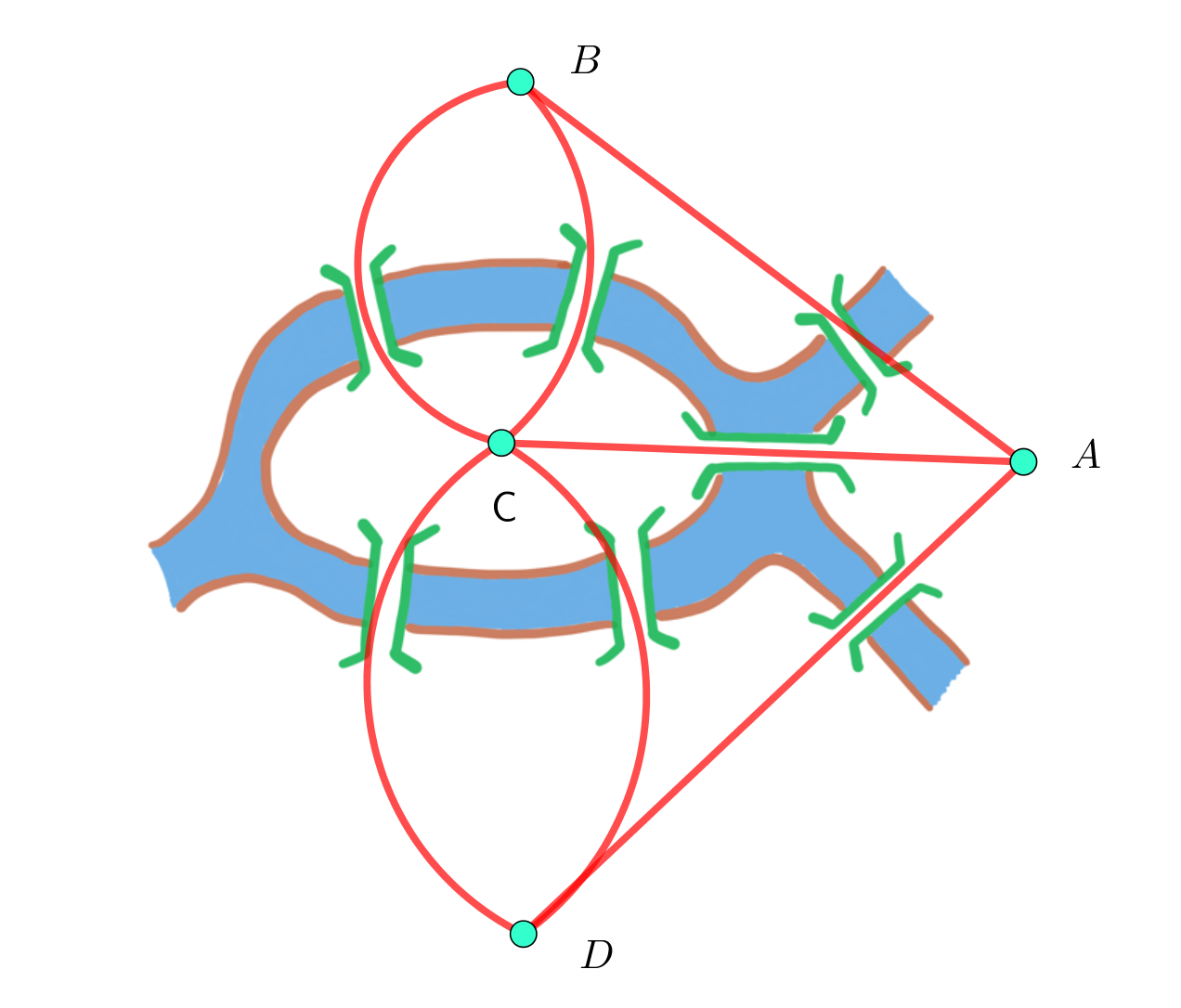
$オイラーは次のように、3段階に分けてこの問題を考えました。$
$(1)\ \ 問題の図をできるだけ単純なものに書き直す。$
$\hspace{2em}すなわちつながっている部分は一つの点に置き換えて$
$\hspace{2em}A,B,C,Dとする。$
$(2)\ \ 7つの橋を4つの点を結ぶ線分や弧としてとらえる。$
$(3)\ \ この図形が、一筆書きで書けるかどうかを調べる。$
$この点と線からなる図(点線図と名付けましょう)からわかるように$
$奇数点が4個あるから一筆書きは不可能です。$
$もしどの橋でも一つを閉鎖してしまえば難なく1回ずつ全部の橋を$
$渡ることができますし、もうひとつ橋をかけたとしてもよいわけ$
$です。$
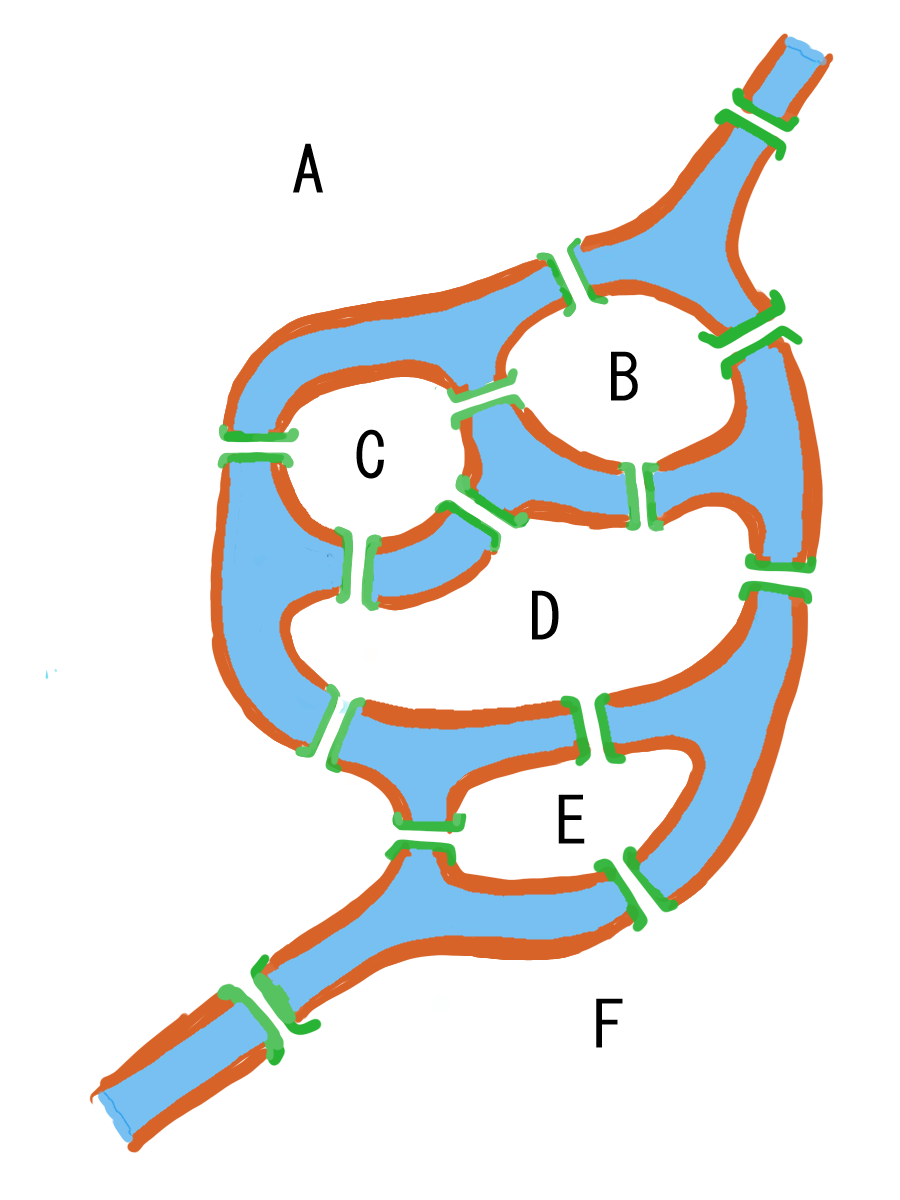
$それでは、私からの橋渡りの問題です。$
$右の図で、同じ橋を二度は通らないようにして、この14の橋を全部渡る$
$ことができるでしょうか。$
$考えるだけでもいやになりますね。$
$このように、複雑な図形で点線図を書くのは大変ですから、各点から出る$
$線分の数を表にまとめるとわかりやすくなります。$
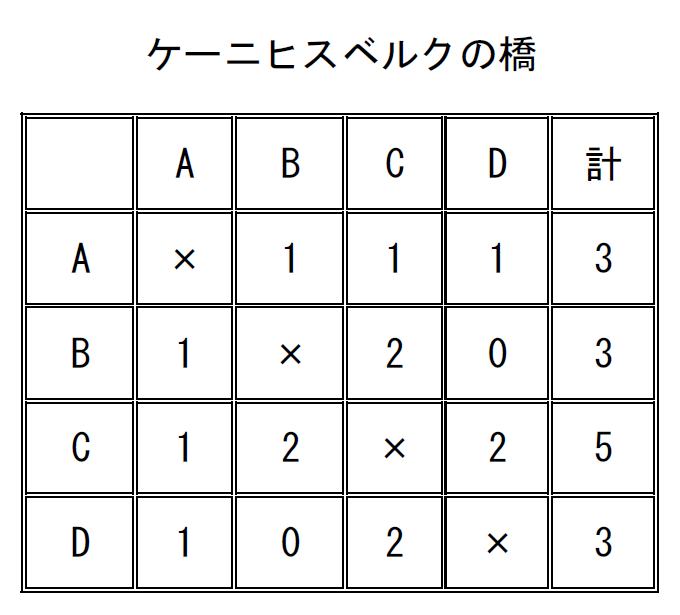
$\quad ケーニヒスベルグの橋の問題で、この表は左図のとおりです。$
$\quad 4つの点はすべて奇数点であることがわかります。$
$同様にして、この橋の問題を表にまとめてみると$
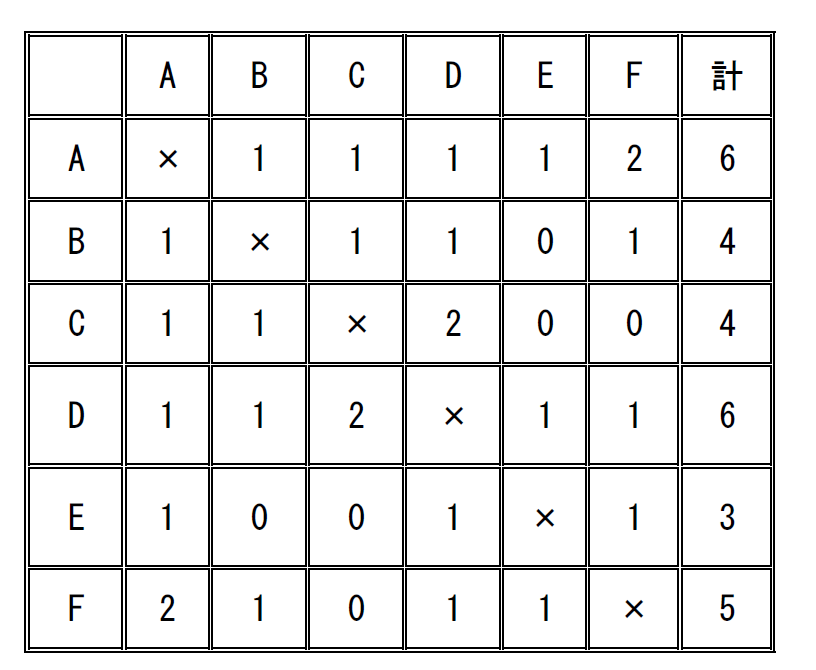
$奇数点がE,F2つありますから一筆書き可能であることがわかります。$
$例えば、Fから出発して、Eがゴールとなるようなルートの取り方は$
$\qquad F \rightarrow A \rightarrow F \rightarrow B \rightarrow A \rightarrow C \rightarrow B \rightarrow D \rightarrow A \rightarrow E \rightarrow F$
$\qquad \rightarrow D \rightarrow C \rightarrow D \rightarrow E$
$なお、一筆書きの問題は、現在ではグラフ理論やネットワーク理論として完成されています。$
メインメニュー に戻る