数学的帰納法による証明
$自然数 \ n\ についての命題 \ P(n)\ の数学的帰納法による証明は$
(i)$\ \ n=1\ のとき成りたつ。$
(ii)$\ \ n=k\ のとき成りたつとすると、n=k+1\ のときも成りたつ。$
$よって、すべての自然数 \ n\ について命題 \ P(n)\ は成りたつ。$
$とします。いわゆる将棋倒しのイメージです。図式で示すと次のとおりです。$
$\qquad P(1) \rightarrow P(2) \rightarrow P(3) \rightarrow \cdots \rightarrow P(k) \rightarrow P(k+1)\rightarrow \cdots $
$数学的帰納法による証明パターンはこの他に$
(i) $n=1,\ n=2\ のとき成りたつ。$
(ii)$n=k,\ n=k+1\ のとき成りたつとすると、n=k+2\ のときも成りたつ。$
$よって、すべての自然数 \ n\ について成りたつ。$
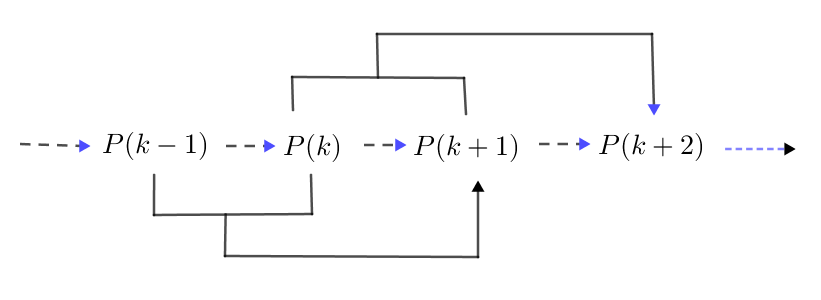
$のように、2つの仮定から結論を導く方法もあります。図式で示すと次のとおりです。$
$\qquad $
$例 \quad 命題:nが自然数のとき、x^n+\cfrac{1}{x^n} \ \ は \ \ x+\cfrac{1}{x}\ のn次式で表される。$
$(証明)$
$\quad X=x+\cfrac{1}{x} \ \ とおく$
(i)$\ \ n=1\ のとき 明らかに成りたつ。$
$\qquad n=2\ のとき \qquad x^2+\cfrac{1}{x^2}=(x+\cfrac{1}{x})^2-2=X^2-2 \quad はXの2次式だから成りたつ。$
(ii)$\ \ n=k,\ \ n=k+1\ のとき成りたつとすると$
$\hspace{4em} x^k+\cfrac{1}{x^k} ,\quad x^{k+1}+\cfrac{1}{x^{k+1}}\ \ はそれぞれXのk次式、k+1次式で表されるから$
$\hspace{4em} x^k+\cfrac{1}{x^k}=b_0X^k+b_1X^{k-1}+ \cdots +b_k$
$\hspace{4em} x^{k+1}+\cfrac{1}{x^{k+1}}=a_0X^{k+1}+a_1X^k+ \cdots +a_{k+1}$
$とおける。このとき$
$\qquad x^{k+2}+\cfrac{1}{x^{k+2}}$
\begin{eqnarray*} &=&(x+\cfrac{1}{x})(x^{k+1}+\cfrac{1}{x^{k+1}})-(x^k+\cfrac{1}{x^k})\\ \\ &=&X(a_0X^{k+1}+a_1X^k+ \cdots +a_kX+a_{k+1})-(b_0X^k+b_1X^{k-1}+ \cdots +b_{k-1}X+b_k)\\ \\ &=&a_0X^{k+2}+a_1X^{k+1}+(a_2-b_0)X^k+ \cdots +(a_{k+1}-b_{k-1})X-b_k\\ \end{eqnarray*}
$\qquad よって \quad x^{k+2}+\cfrac{1}{x^{k+2}}\ \ はXのk+2次式である。$
(i),(ii)$\ \ より、すべての自然数nについて、x^n+\cfrac{1}{x^n}\ は \ x+\cfrac{1}{x}\ のn次式で表される。$
$例えば \ \ n=3 \ のとき$
$\qquad x^3+\cfrac{1}{x^3}=(x+\cfrac{1}{x})(x^2+\cfrac{1}{x^2})-(x+\cfrac{1}{x})=X(X^2-2)-X=X^3-3X$
$あるいは$
$\qquad x^3+\cfrac{1}{x^3}=(x+\cfrac{1}{x})^3-3x\times \cfrac{1}{x}(x+\cfrac{1}{x})=X^3-3X$
$また \quad t_n=x^n+\cfrac{1}{x^n} \quad とおくと$
$証明につかった \quad x^{n+2}+\cfrac{1}{x^{n+2}}=(x+\cfrac{1}{x})(x^{n+1}+\cfrac{1}{x^{n+1}})-(x^n+\cfrac{1}{x^n}) \ \ より$
$\hspace{3em} t_{n+2}=t_1t_{n+1}-t_n$
$なる隣接3項間の漸化式が得られる。ただし \ \ t_1=X,\quad t_2=X^2-2$
$この漸化式をつかって計算すると$
$\qquad x^3+\cfrac{1}{x^3}=t_3=t_1t_2-t_1=X(X^2-2)-X=X^3-3X$
$\qquad x^4+\cfrac{1}{x^4}=t_4=t_1t_3-t_2=X(X^3-3X)-(X^2-2)=X^4-4X^2+2$
$と順次求めることができます。$
メインメニュー に戻る