茨城大学(数学) 2025年 問題3
$i\ を虚数単位とし、z\ を複素数とする。また、w=1+iz \ \ とする。複素数平面において、4\ 点O(0),\ \ A(z),$
$B(w),\ \ C(1) \ \ を考える。以下の各問に答えよ。$
$(1)\ \ OA=BC \ \ であることを示せ。また、z \ne 0 \ \ のとき、直線 \ OA\ と直線 \ BC\ は垂直に交わることを示せ。$
$(2)\ \ OA=AB \ \ を満たす点 \ z\ の全体は、どのような図形を表すか。$
$(3)\ \ 点 \ Z\ が(2)の図形上を動くとき、|z+w|\ \ の最大値と最小値を求めよ。ただし、最大値と最小値を与える$
$\quad z\ の値を求める必要はない。$
(1)
$OA=|z|$
$BC=|1-w|=|1-(1+iz)|=|-iz|=|z|$
$\therefore \ \ OA=BC$
$\arg (BC)=\arg(1-w)=\arg(-iz)=\arg(-i)+\arg(z)=-\dfrac{\pi}{2}+\arg(OA)$
$\therefore \arg(OA)-\arg(BC)=\dfrac{\pi}{2}$
$よって \quad OA \perp BC$
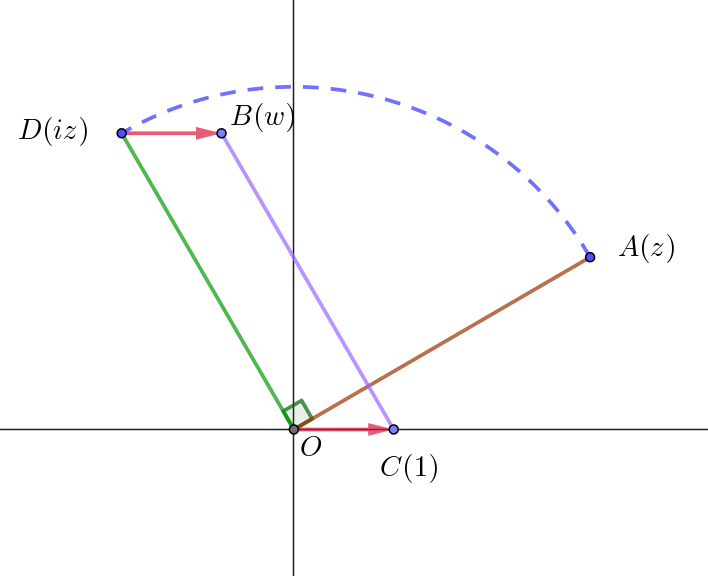
$点A(z)\ を原点 \ O\ のまわりに \ \ \dfrac{\pi}{2}\ 回転した点は \ D(iz)\ \ だから$
$点B(1+iz) \ \ は点D(iz)\ \ を \ 1\ 平行移動した点である。$
$点C(1)\ \ も原点(O)\ を \ 1\ 平行移動した点であるから$
$線分BC\ は線分DO \ を平行移動したものである。$
$したがって\quad OA=OD=BC,\quad OA \perp BC$
(2)
$z=x+yi \ \ (x,\ y\ は実数)\ \ とおくと$
$OA^2=|z|^2=x^2+y^2$
$AB^2=|w-z|^2=|1+iz-z|^2=|1+(i-1)(x+yi)|^2=|1-x-y+i(x-y)|^2=(1-x-y)^2+(x-y)^2$
$OA=AB \ \ より$
$x^2+y^2=(1-x-y)^2+(x-y)^2$
$1-2(x+y)+(x+y)^2-2xy=0$
$x^2+y^2-2x-2y+1=0$
$(x-1)^2+(y-1)^2=1$
$よって \quad z\ の全体は、(1+i)\ を中心とし、半径 \ 1\ の円を表す。$
$(別解)$
$OA=AB \ \ より \quad |z|=|w-z| \qquad |z|=|1+(-1+i)z|$
$|z|=|-1+i|\big|z+\dfrac{1}{-1+i}\big|$
$|z|=\sqrt{2}\big|z-\dfrac{1+i}{2}\big|$
$これより \ \ z\ は円(アポロニウスの円)をえがくことがわかる。$
$両辺を平方して$
$z\overline{z}=2\big(z-\dfrac{1+i}{2}\big)\big(\overline{z}-\dfrac{1-i}{2}\big)$
$z\overline{z}=2z\overline{z}-(1-i)z-(1+i)\overline{z}+1$
$z\overline{z}-(1-i)z-(1+i)\overline{z}+1=0$
$(z-(1+i))(\overline{z}-(1-i))=1$
$(z-(1+i))(\overline{z-(1+i)}=1$
$|z-(1+i)|^2=1$
$|z-(1+i)|=1$
$よって \ \ z\ の全体は、(1+i)\ を中心とし、半径 \ 1\ の円を表す。$
(3)
$よって \quad |z+w|\ は \ A(z)\ と点(\dfrac{-1+i}{2})\ の距離の \ \sqrt{2}\ 倍である。$
<
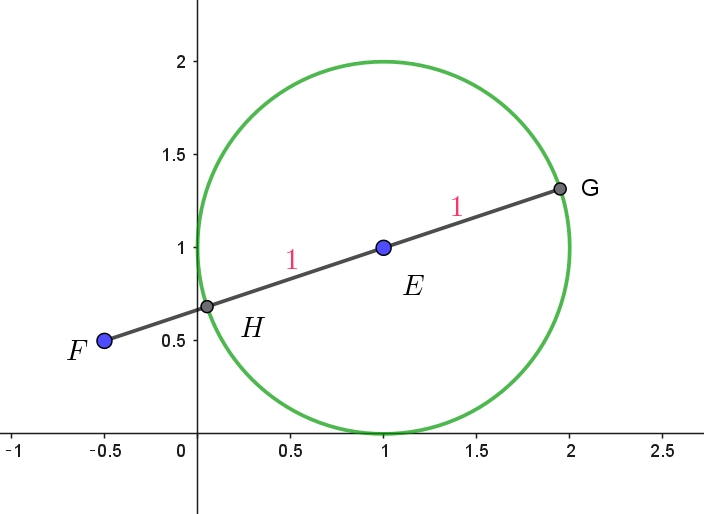
$円の中心を \ E(1+i),\ \ F(\dfrac{-1+i}{2})\ \ とすると$
$FE=\big|(1+i)-\dfrac{-1+i}{2}\big|=\big|\dfrac{3}{2}+\dfrac{1}{2}i\big|=\dfrac{\sqrt{10}}{2}$
$円と直線FE \ の交点を右図のように \ G,\ H\ \ とすると$
$|z+w|\ \ の$
$最大値は \quad \sqrt{2}FG=\sqrt{2}(FE+EG)=\sqrt{2}(\dfrac{\sqrt{10}}{2}+1)=\sqrt{5}+\sqrt{2}$
$最小値は \quad \sqrt{2}FH=\sqrt{2}(FE-HE)=\sqrt{2}(\dfrac{\sqrt{10}}{2}-1)=\sqrt{5}-\sqrt{2}$
$(別解)$
$z=x+yi \ \ (x,\ y \ は実数)\ \ とおくと$
\begin{eqnarray*} |z+w|^2 &=&|z+1+iz|^2\\ \\ &=&|x+yi+1+i(x+yi)|^2\\ \\ &=&|x-y+1+i(x+y)|^2\\ \\ &=&(x-y+1)^2+(x+y)^2\\ \\ &=&(x-y)^2+2(x-y)+1+(x+y)^2\\ \\ &=&2(x^2+y^2)+2(x-y)+1\\ \end{eqnarray*} $点 \ Z\ が(2)の図形上を動くとき、(x-1)^2+(y-1)^2=1 \quad だから$
$x=1+\cos \theta, \quad y=1+\sin \theta \quad とおける。$
\begin{eqnarray*} |z+w|^2 &=&2(x^2+y^2)+2(x-y)+1\\ \\ &=&2\big((1+\cos \theta)^2+(1+\sin \theta)^2\big)+2\big((1+\cos \theta)-(1+\sin \theta)\big)+1\\ \\ &=&2(1+2\cos \theta +\cos ^2\theta)+2(1+2\sin \theta+\sin^2\theta)+2(\cos \theta -\sin \theta)+1\\ \\ &=&2\sin \theta+ 6\cos \theta +7\\ \\ &=&\sqrt{40}\big(\dfrac{2}{\sqrt{40}}\sin \theta + \dfrac{6}{\sqrt{40}}\cos \theta)\big)+7\\ \end{eqnarray*} $ここで、\cos \alpha =\dfrac{2}{\sqrt{40}} , \quad \sin \alpha = \dfrac{6}{\sqrt{40}} \quad とおいて合成すると$
\begin{eqnarray*} |z+w|^2 &=&2\sqrt{10}(\cos \alpha \sin \theta + \sin \alpha \cos \theta)+7\\ \\ &=&2\sqrt{10}\sin(\theta +\alpha)+7\\ \\ \end{eqnarray*} $よって \quad |z+w|\ \ の$
$最大値は \quad \sqrt{2\sqrt{10}+7}=\sqrt{5}+\sqrt{2}$
$最小値は \quad \sqrt{-2\sqrt{10}+7}=\sqrt{5}-\sqrt{2}$
メインメニュー に戻る