茨城大学(数学) 2025年 問題2
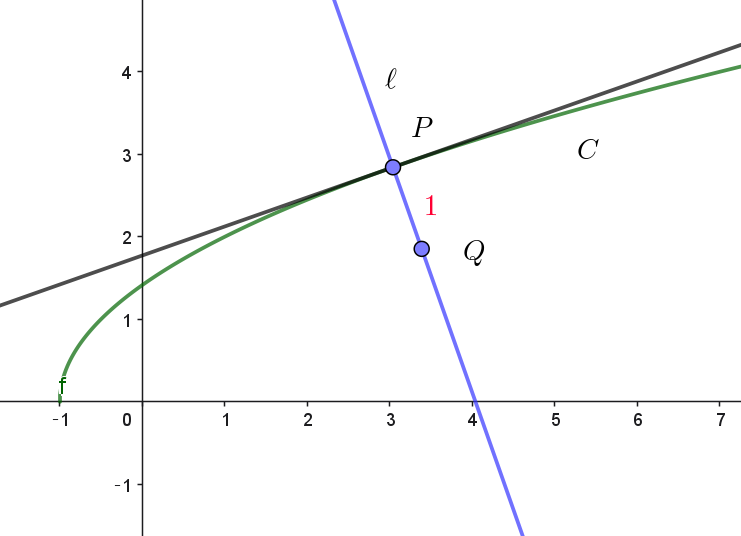
$a > 0,\ \ f(x)=\sqrt{2(x+1)}\ \ とする。座標平面において、曲線 \ C:y=f(x)\ \ 上の点P(\dfrac{a^2}{2}-1,\ a)\ を通る \ C\ の$
$法線を \ \ell \ とする。また、点Q(s,\ t)\ は法線 \ \ell \ 上にあり、PQ=1 \ \ かつ \ \ t < a\ \ を満たすとする。$
$以下の各問に答えよ。$
$(1)\ \ 導関数 \ f'(x)\ を求めよ。また、法線 \ \ell \ の方程式を求めよ。$
\[(2)\ \ s\ および \ t\ を \ a\ を用いて表せ。また、極限 \ \ \lim_{a \rightarrow +0} s \ \ を求めよ。\]
$(3)\ \ n\ を \ 0\ 以上の整数とする。a \longrightarrow +0 \ \ のとき、 \dfrac{t}{a^n} \ \ が収束するような \ n\ の値をすべて求めよ。また、$
$\quad そのときの極限値をそれぞれ求めよ。$
(1)
$f'(x)=\dfrac{2}{2\sqrt{2(x+1)}}=\dfrac{1}{\sqrt{2(x+1)}}$
$a > 0 \ \ だから \quad f'(\dfrac{a^2}{2}-1)=\dfrac{1}{\sqrt{2 \times \dfrac{a^2}{2}}}=\dfrac{1}{a}$
$よって \quad 法線 \ \ell \ の傾きは \ -a\ だから、その方程式は$
$y=-a\big(x-(\dfrac{a^2}{2}-1)\big)+a$
$\therefore \ \ y=-ax+\dfrac{a^3}{2}$
(2)
$点Q(s,\ t)\ は法線 \ \ell \ 上にあるから$
$t=-as+\dfrac{a^3}{2} \hspace{18em}①$
$PQ=1 \ \ より \quad (s-\dfrac{a^2}{2}+1)^2+(t-a)^2=1 \hspace{5em}②$
$①を②に代入して$
$(s-\dfrac{a^2}{2}+1)^2+\big(-as+\dfrac{a^3}{2}-a \big)^2=1$
$(s+1-\dfrac{a^2}{2})^2+a^2\big(s+1-\dfrac{a^2}{2} \big)^2=1$
$(a^2+1)\big(s+1-\dfrac{a^2}{2}\big)^2 =1$
$\big(s+1-\dfrac{a^2}{2}\big)^2 =\dfrac{1}{a^2+1}$
$a > 0 \ \ かつ \ \ t < a\ \ を満たすから①より \quad -as+\dfrac{a^3}{2} < a $
$-s+\dfrac{a^2}{2} < 1 \qquad \therefore s+1-\dfrac{a^2}{2} > 0 $
$よって \quad s+1-\dfrac{a^2}{2} =\dfrac{1}{\sqrt{a^2+1}}$
$s=\dfrac{a^2}{2}-1+\dfrac{1}{\sqrt{a^2+1}}$
$①に代入して$
$t=-a \times \big(\dfrac{a^2}{2}-1+\dfrac{1}{\sqrt{a^2+1}}\big) +\dfrac{a^3}{2}=a-\dfrac{a}{\sqrt{a^2+1}}$
\[\lim_{a \rightarrow +0} s=\lim_{a \rightarrow +0} \big(\dfrac{a^2}{2}-1+\dfrac{1}{\sqrt{a^2+1}}\big)=-1+1=0\]
(3)
$(2)より \quad t=a-\dfrac{a}{\sqrt{a^2+1}} \ \ だから \quad a \longrightarrow +0 \ \ とすると$
(i)$\ \ n=0 \ \ のとき$
$\quad \dfrac{t}{a^n}=t=a-\dfrac{a}{\sqrt{a^2+1}} \longrightarrow 0$
(ii)$\ \ n=1 \ \ のとき$
$\quad \dfrac{t}{a^n}=\dfrac{t}{a}=1-\dfrac{1}{\sqrt{a^2+1}} \longrightarrow 1-1=0$
(iii)$\ \ n=2 \ \ のとき$
\begin{eqnarray*} \dfrac{t}{a^n} &=&\dfrac{t}{a^2}\\ \\ &=&\dfrac{1}{a}\big(1-\dfrac{1}{\sqrt{a^2+1}}\big)\\ \\ &=&\dfrac{\sqrt{a^2+1}-1}{a\sqrt{a^2+1}}\\ \\ &=&\dfrac{(a^2+1)-1}{a\sqrt{a^2+1}(\sqrt{a^2+1}+1)}\\ \\ &=&\dfrac{a}{\sqrt{a^2+1}(\sqrt{a^2+1}+1)}\\ \\ & & \longrightarrow 0 \end{eqnarray*} (iv)$\ \ n=3\ \ のとき$
$\quad \dfrac{t}{a^n}=\dfrac{t}{a^3}=\dfrac{1}{\sqrt{a^2+1}(\sqrt{a^2+1}+1)} \longrightarrow \dfrac{1}{2}$
(v)$\ \ n \geqq 4 \ \ のとき$
$\quad \dfrac{t}{a^n}=\dfrac{1}{a^{n-3}\sqrt{a^2+1}(\sqrt{a^2+1}+1)} \longrightarrow +\infty$
$したがって \quad 収束するような \ n\ の値は、0,\ \ 1,\ \ 2,\ \ 3$
$そのときの極限値は$
\[ \hspace{1em} \lim_{a \rightarrow +0}\dfrac{t}{a^n}= \left\{ \begin{array}{l} 0 \hspace{5em}(n=0,1,2)\\ \dfrac{1}{2} \hspace{5em}(n=3)\\ \end{array} \right. \]
メインメニュー に戻る