茨城大学(数学) 2025年　問題1


$座標平面において、曲線 \ C:y=(x-2)^2 \ \ と、C\ 上の点A(2,\ 0)\ を通る傾き \ a\ の直線 \ \ell \ を考える。ただし、$
$a > 0 \ とする。曲線 \ C\ と \ y\ 軸および直線 \ \ell \ で囲まれた\ 図形を \ D_1\ とし、曲線 \ C\ と直線 \ \ell \ で囲まれた図形を$
$D_2\ とする。D_1,\ D_2 \ を \ y\ 軸のまわりに \ 1\ 回転してできる立体の体積をそれぞれ \ V_1(a),\ V_2(a)\ とする。$
$以下の各問に答えよ。$
$(1)\ \ 曲線 \ C\ と直線 \ \ell \ の交点のうち、点A\ と異なる点の座標を \ a\ を用いて表せ。$
$(2)\ \ V_1(a) \ および \ V_2(a)\ を求めよ。$
$(3)\ \ V(a)=V_1(a)-V_2(a) \ \ とする。関数 \ V(a) \ の極値を求めよ。$
$(4)\ \ 0 < a < 2 \ \ のとき、図形 \ D_1\ を \ x\ 軸のまわりに \ 1\ 回転してできる立体の体積を \ a\ を用いて表せ。$


(1)

　

$点A(2,\ 0)\ を通る傾き \ a\ の直線 \ \ell \ は$

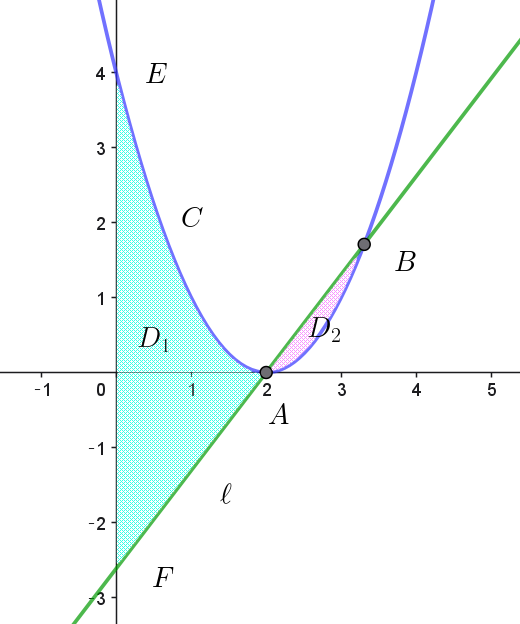
$y=a(x-2) \ \ だから、曲線 \ C\ と直線 \ \ell \ の交点 \ B\ の \ x\ 座標は$

$(x-2)^2=a(x-2) \ \ の解である。$

$(x-2)(x-2-a)=0$

$点A(2,\ 0)\ と異なる点の\ x座標は \quad x=a+2$

$よって \quad B(a+2,\ a^2)$


(2)


$曲線 \ C\ と直線 \ \ell \ の \ y\ 軸との交点はそれぞれ$

$E(0,\ 4),\ \ F(0,\ -2a)\ \ だから$

$図形 \ D_1\ を \ y\ 座標が \ \ [-2a,\ 0],\ \ [0,\ 4]\ \ の部分に分割すると$

$[-2a,\ 0]\ \ の部分は円錐になることに注意して、その体積は$

$\dfrac{1}{3}\times \pi OA^2 \times OF=\dfrac{\pi}{3}\times 2^2 \times 2a=\dfrac{8}{3}\pi a$

$[0,4] \ \ の部分は \quad x=2-\sqrt{y} \quad だからその体積は$
\begin{eqnarray*} & &\pi\int_0^4(2-\sqrt{y})^2dy\\ \\ &=&\pi\int_0^4(4-4\sqrt{y}+y)dy\\ \\ &=&\pi\big[4y-\dfrac{8}{3}y^{\scriptsize{\dfrac{3}{2}}}+\dfrac{1}{2}y^2\big]_0^4\\ \\ &=&\big(16-\dfrac{8}{3} \times 4^{\scriptsize{\dfrac{3}{2}}}+8\big)\pi\\ \\ &=&\dfrac{8}{3}\pi \end{eqnarray*}
$よって \quad V_1(a)=\dfrac{8}{3}\pi a+ \dfrac{8}{3}\pi=\dfrac{8}{3}\pi (a+1)$

$図形 \ D_2\ は曲線 \ C\ が \ \ x=2+\sqrt{y} ,\ \ 直線 \ \ell \ が \ \ x=2+\dfrac{y}{a}\ \ だから$

\begin{eqnarray*} V_2(a) &=&\pi\int_0^{a^2} (2+\sqrt{y})^2dy -\pi\int_0^{a^2} \big(2+\dfrac{y}{a}\big)^2dy\\ \\ &=&\pi\int_0^{a^2} \big((4+4\sqrt{y}+y) -(4+\dfrac{4}{a}y+\dfrac{y^2}{a^2})\big)dy\\ \\ &=&\pi\int_0^{a^2} \big(4\sqrt{y}+(1-\dfrac{4}{a})y-\dfrac{y^2}{a^2}\big)dy\\ \\ &=&\pi\big[\dfrac{8}{3}y^{\scriptsize{\dfrac{3}{2}}}+\dfrac{1}{2}(1-\dfrac{4}{a})y^2-\dfrac{y^3}{3a^2}\big]_0^{a^2}\\ \\ &=&\pi \big(\dfrac{8}{3}a^3+\dfrac{1}{2}(1-\dfrac{4}{a})a^4-\dfrac{a^6}{3a^2}\big)\\ \\ &=&\pi \big(\dfrac{8}{3}a^3+\dfrac{1}{2}a^4-2a^3-\dfrac{a^4}{3}\big)\\ \\ &=&\dfrac{\pi a^3}{6}(a+4) \end{eqnarray*}

(3)


\begin{eqnarray*} V(a) &=&V_1(a)-V_2(a)\\ \\ &=&\dfrac{8}{3}\pi (a+1) - \dfrac{\pi a^3}{6}(a+4)\\ \\ &=&-\dfrac{\pi}{6}(a^4+4a^3-16a-16)\\ \\ &=&-\dfrac{\pi}{6}(a+2)^3(a-2) \end{eqnarray*}
\begin{eqnarray*} V'(a) &=&-\dfrac{\pi}{6} \big(3(a+2)^2(a-2)+(a+2)^3\big)\\ \\ &=&-\dfrac{\pi}{6}(a+2)^2\big(3(a-2)+(a+2)\big)\\ \\ &=&-\dfrac{2\pi}{3} (a+2)^2(a-1) \end{eqnarray*}
$V'(a)=0 \ \ より \ \ a > 0 \ \ だから \quad a=1$

　

$増減表$
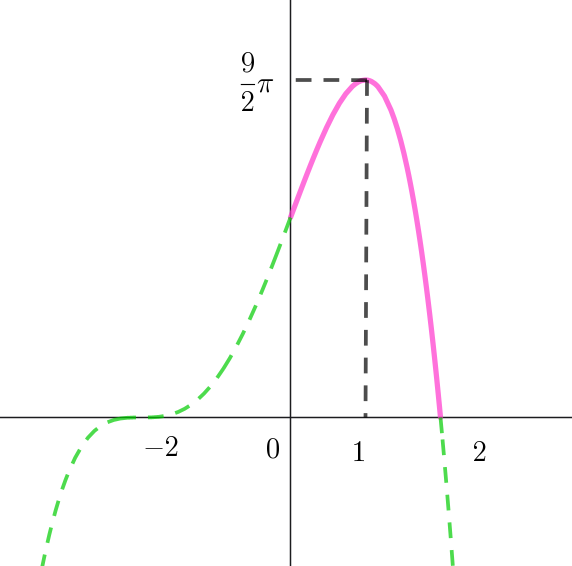
\[ \begin{array}{c||c|c|c|c|c} a& 0 & \cdots & 1 & \cdots \\ \hline V'(a) & & + & 0 & - \\ \hline V(a) & & \nearrow & 極大 & \searrow \\ \end{array} \]
$V(a)\ は \ a=1\ \ で極大となり、極大値$

$V(1)=- \dfrac{\pi}{6} \times 3^3 \times (-1)=\dfrac{9}{2}\pi \ \ をもつ$

$なお、V(a)\ のグラフは右図のとおり$


(4)

　

$\ell : y=a(x-2)\ を \ x\ 軸について折り返すと$

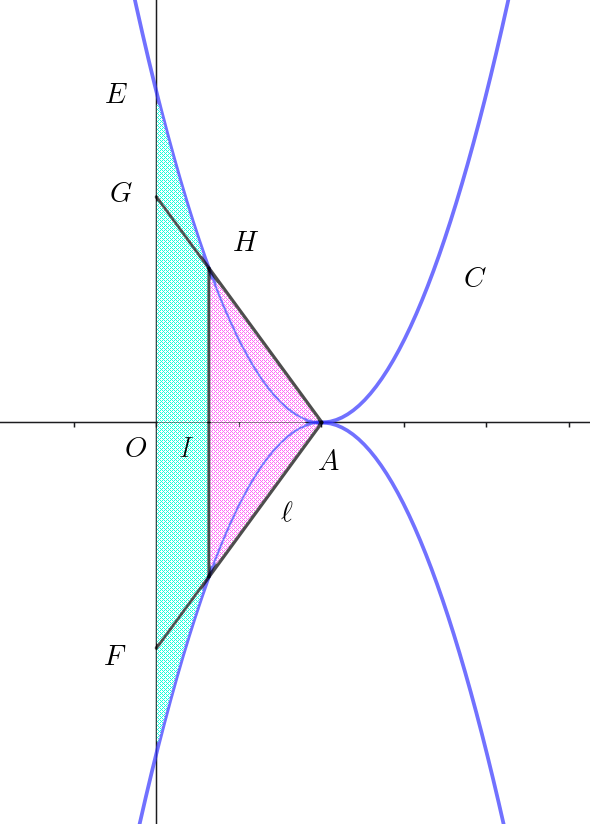
$-y=a(x-2) \qquad \ell ' : y=-a(x-2)$

$C\ と \ \ell ' \ の点 \ A\ 以外の共有点 \ H\ の座標は$

$(x-2)^2=-a(x-2)$

$(x-2)(x-2+a)=0$

$x=2-a,\quad y=(-a)^2=a^2 \qquad H(2-a,\ a^2)$

$0 < a < 2 \ \ だから \quad 0 < 2-a < 2$

$よって 点 \ H\ は線分 \ AG\ 上にある。$

$図形 \ D_1\ を \ x\ 軸のまわりに \ 1\ 回転してできる回転体のうち$

$線分\ AH\ による、底面の半径 \ HI,高さ \ AI\ の円錐の体積 \ V_3\ は$

$V_3=\dfrac{1}{3} \times \pi HI^2 \times AI=\dfrac{\pi}{3}(a^2)^2 \times a=\dfrac{\pi}{3}a^5$

$曲線 \ C\ の \ [0,\ 2-a] \ の部分による体積 \ V_4\ は$

\begin{eqnarray*} V_4 &=&\pi \int_0^{2-a}(x-2)^4dx\\ \\ &=&\pi\big[\dfrac{(x-2)^5}{5}]_0^{2-a}\\ \\ &=&\dfrac{\pi}{5}\big((-a)^5-(-2)^5\big)\\ \\ &=&\dfrac{\pi}{5}(-a^5+32)\\ \end{eqnarray*}
$よって求める体積 \ V\ は$

$V=V_3+V_4=\dfrac{\pi}{3}a^5+\dfrac{\pi}{5}(-a^5+32)=\dfrac{\pi}{15}(2a^5+96)$


ページの先頭へ↑



メインメニュー　に戻る