茨城大学(数学) 2024年　問題3


$半径 \ 1\ の円に内接する正八角形において、その \ 8\ つの頂点のうちの \ 1\ つを \ A\ とする。1\ 個のさいころを \ 1\ 回$
$投げ、出た目が \ x\ ならば、正八角形の \ 8\ つの頂点のうち \ A\ から反時計回りに \ x\ 個先にあるものを \ B\ とする。$
$さらに、１\ 個のさいころを \ 1\ 回投げ、出た目が \ y\ ならば、正八角形の \ 8\ つの頂点のうち \ B\ から反時計回り$
$に \ y\ 個先にあるものを \ C\ とする。以下の各問に答えよ。ただし、正八角形が円に内接するとは、正八角形の$
$すべての頂点がその円周上にあることをいう。$
$(1)\ \ 3点 \ A,\ B,\ C\ が三角形の \ 3\ つの頂点となる確率 \ p_1\ を求めよ。$
$(2)\ \ 3点 \ A,\ B,\ C\ が直角三角形の \ 3\ つの頂点となる確率 \ p_2\ を求めよ。$
$(3)\ \ 3点 \ A,\ B,\ C\ が三角形の \ 3\ つの頂点となるとき、その三角形の面積を \ S\ とする。S\ のとり得る値をすべて$
$\quad 求めよ。また、S\ のとり得る値の最大値を求めよ。$


(1)

　

$1\ 回目に出た目\ x\ 、2\ 回目に出た目\ y\ を\ (x,\ y)\ と表すことにする。$

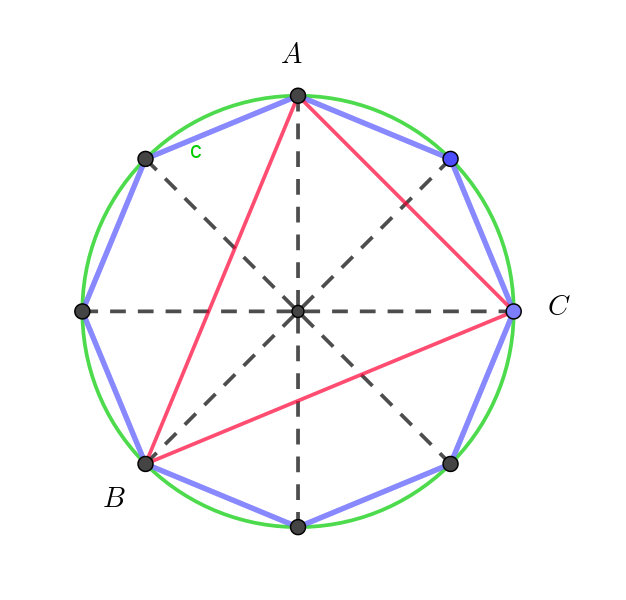
$右図は\ (3,\ 3)\ のときにできる三角形である。$

$このように、3点 \ A,\ B,\ C\ が三角形の \ 3\ つの頂点となるのは$

$(1,\ 1),\ (1,\ 2),\ (1,\ 3),\ (1,\ 4),\ (1,\ 5),\ (1,\ 6)$

$(2,\ 1),\ (2,\ 2),\ (2,\ 3),\ (2,\ 4),\ (2,\ 5)$

$(3,\ 1),\ (3,\ 2),\ (3,\ 3),\ (3,\ 4),\ (3,\ 6)$

$(4,\ 1),\ (4,\ 2),\ (4,\ 3),\ (4,\ 5),\ (4,\ 6)$

$(5,\ 1),\ (5,\ 2),\ (5,\ 4),\ (5,\ 5),\ (5,\ 6)$

$(6,\ 1),\ (6,\ 3),\ (6,\ 4),\ (6,\ 5),\ (6,\ 6)$

$以上の \ 31\ 通りだから \quad p_1=\cfrac{31}{36}$


(2)


$(1)の三角形のうち、直角三角形は次の2\ パターンがある。$

$\hspace{3em}$
$\hspace{6em}$


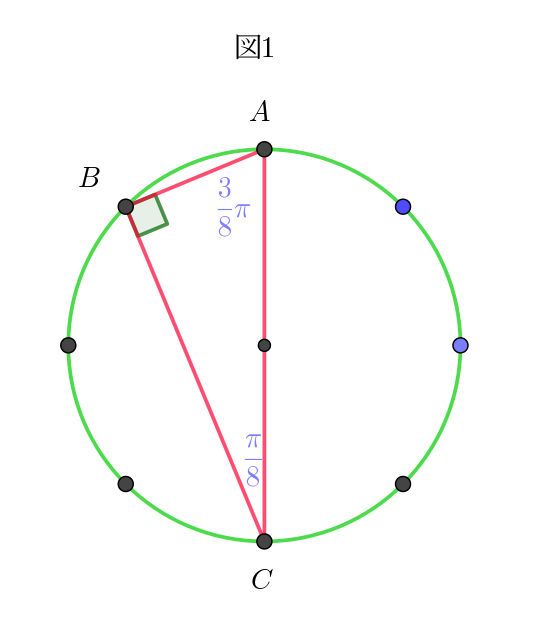
(i)$\ \ 図1は、(1,\ 3),\ \ (1,\ 4),\ \ (3,\ 1),\ \ (3,\ 4),\ \ (4,\ 1),\ \ (4,\ 3),\ \ (4,\ 5),\ \ (5,\ 4)\ \ の場合で$

$\qquad 内角が、\cfrac{\pi}{8},\ \ \cfrac{3}{8}\pi,\ \ \cfrac{\pi}{2}\ \ の直角三角形。$

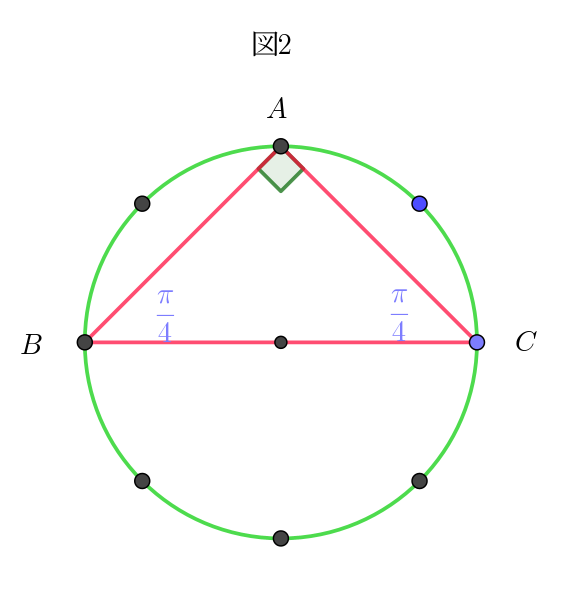
(ii)$\ \ 図2は、(2,\ 2),\ \ (2,\ 4),\ \ (4,\ 2),\ \ (4,\ 6),\ \ (6,\ 4),\ \ (6,\ )\ \ の場合で$

$\qquad 内角が、\cfrac{\pi}{4},\ \ \cfrac{\pi}{4},\ \ \cfrac{\pi}{2}\ \ の直角三角形。$

(i),(ii)$\ \ 全部で \quad 14\ 個だから \quad p_2=\cfrac{14}{36}=\cfrac{7}{18}$


(3)

　

$三角形の面積を求めるために、弦の長さを余弦定理を用いて求める。$

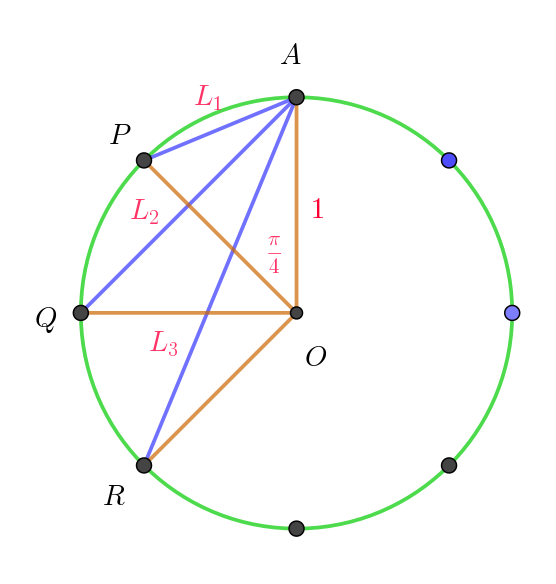
(i)$\ \ 頂点と隣の頂点を結んだ弦の長さL_1は$

$\quad L_1=\sqrt{1^2+1^2-2 \times 1 \times 1 \times \cos \dfrac{\pi}{4}}=\sqrt{2-\sqrt{2}}$

(ii)$\ \ 頂点と2つ先の頂点を結んだ弦の長さL_2は$

$\quad L_2=\sqrt{1^2+1^2}=\sqrt{2}$

(iii)$\ \ 頂点と3つ先の頂点を結んだ弦の長さL_3は$

$\quad L_3=\sqrt{1^2+1^2-2 \times 1 \times 1 \times \cos \dfrac{3}{4}\pi}=\sqrt{2+\sqrt{2}}$


$(1)で調べた\ 31\ 個の三角形を合同な三角形で類別して、それぞれについて面積を求める。$

　

(i)$\ \ (1,\ 1),\ \ (1,\ 6),\ \ (6,\ 1)\ \ のとき図3\ の場合で$

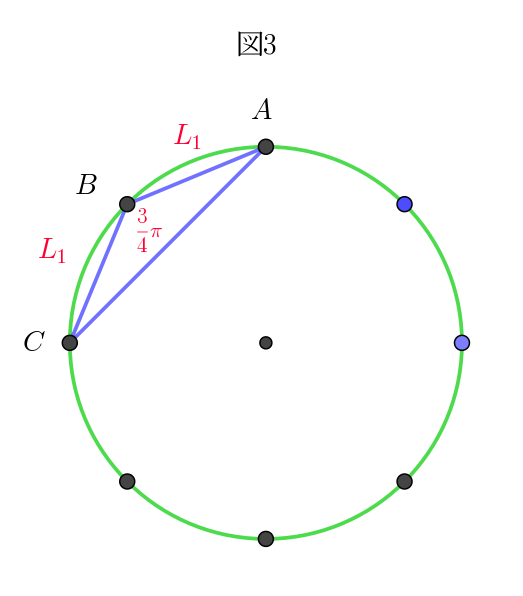
\begin{eqnarray*} S_1 &=&\cfrac{1}{2} \times \sqrt{2-\sqrt{2}} \times \sqrt{2-\sqrt{2}} \times \sin \dfrac{3}{4}\pi\\ \\ &=&\cfrac{1}{2} \times (2-\sqrt{2}) \times \cfrac{1}{\sqrt{2}}\\ \\ &=&\cfrac{\sqrt{2}-1}{2} \end{eqnarray*}
(ii)$\ \ (1,\ 2),\ \ (1,\ 5),\ \ (2,\ 1),\ \ (2,\ 5),\ \ (3,\ 6),\ \ (5,\ 1),\ \ (5,\ 2),\ \ (6,\ 3) \ \ のとき図4\ の場合で$

　

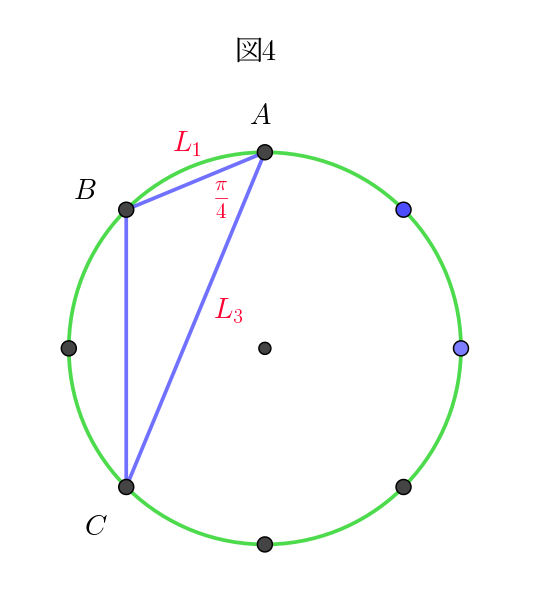
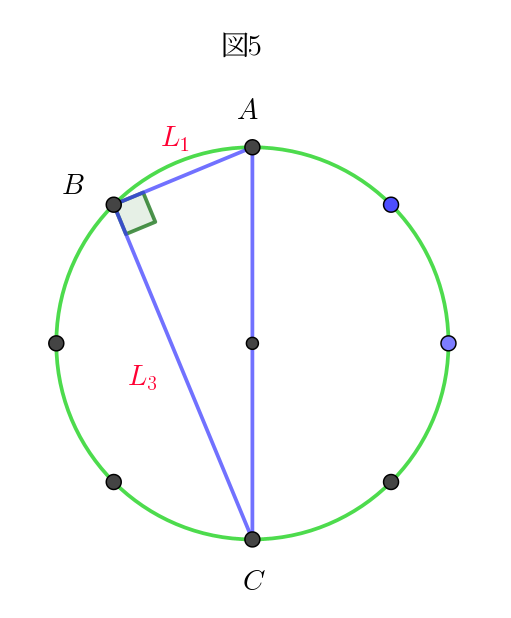
\begin{eqnarray*} S_2 &=&\cfrac{1}{2} \times \sqrt{2-\sqrt{2}} \times \sqrt{2+\sqrt{2}} \times \sin \dfrac{\pi}{4}\\ \\ &=&\cfrac{1}{2} \times \sqrt{4-2} \times \cfrac{1}{\sqrt{2}}\\ \\ &=&\cfrac{1}{2} \end{eqnarray*}
(iii)$\ \ (1,\ 3),\ \ (1,\ 4),\ \ (3,\ 1),\ \ (3,\ 4),\ \ (4,\ 1),\ \ (4,\ 3),\ \ (4,\ 5),\ \ (5,\ 4)\ \ のとき$

$\qquad 図5\ の場合で$

　

\begin{eqnarray*} S_3 &=&\cfrac{1}{2} \times \sqrt{2-\sqrt{2}} \times \sqrt{2+\sqrt{2}} \\ \\ &=&\cfrac{1}{2} \times \sqrt{4-2}\\ \\ &=&\cfrac{\sqrt{2}}{2} \end{eqnarray*}

(iv)$\ \ (2,\ 2),\ \ (2,\ 4),\ \ (4,\ 2),\ \ (4,\ 6),\ \ (6,\ 4),\ \ (6,\ 6)\ \ のとき図6\ の場合で$

　


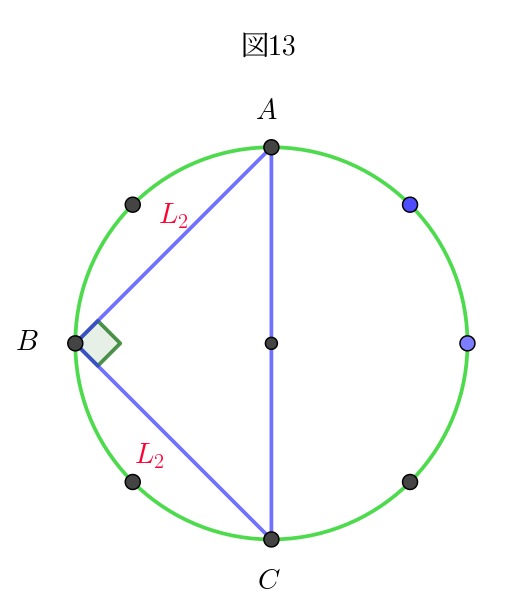
\begin{eqnarray*} S_4 &=&\cfrac{1}{2} \times \sqrt{2} \times \sqrt{2} \\ \\ &=&1 \end{eqnarray*}



(v)$\ \ (2,\ 3),\ \ (3,\ 2),\ \ (3,\ 3),\ \ (5,\ 5),\ \ (5,\ 6),\ \ (6,\ 5)\ \ のとき図7\ の場合で$

　

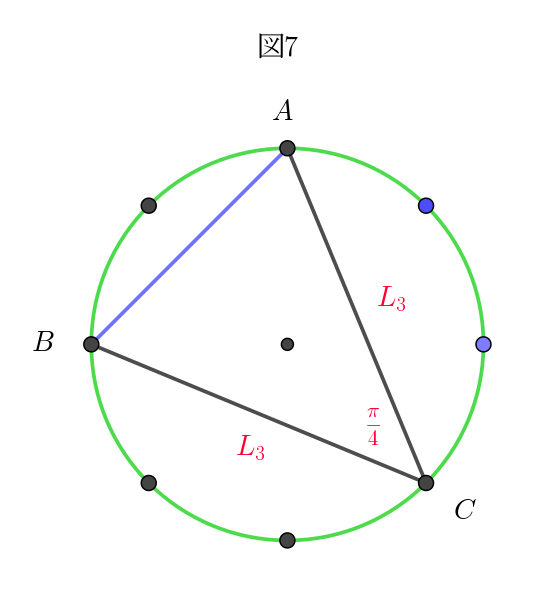
\begin{eqnarray*} S_5 &=&\cfrac{1}{2} \times \sqrt{2+\sqrt{2}} \times \sqrt{2+\sqrt{2}} \times \sin \dfrac{\pi}{4}\\ \\ &=&\cfrac{2+\sqrt{2}}{2} \times \cfrac{1}{\sqrt{2}}\\ \\ &=&\cfrac{\sqrt{2}+1}{2} \end{eqnarray*}
(i)$～$(v)$より \ S\ のとり得る値は \quad \cfrac{\sqrt{2}-1}{2},\quad \cfrac{1}{2},\quad \cfrac{\sqrt{2}}{2}, \quad 1,\quad \cfrac{\sqrt{2}+1}{2} \quad の \ 5\ 通り$

$S\ のとり得る値の最大値は \quad \cfrac{\sqrt{2}+1}{2}$


ページの先頭へ↑



メインメニュー　に戻る