茨城大学(理系) 2024年 問題3
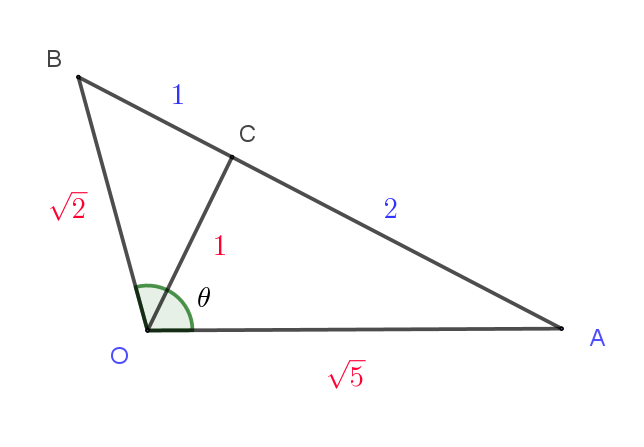
$三角形 \ OAB\ において、OA=\sqrt{5},\ \ OB=\sqrt{2}\ \ とする。辺 \ AB\ を \ 2:1\ に内分する点を \ C\ とおくと \ OC=1$
$であった。\vec{OA}=\vec{a},\ \ \vec{OB}=\vec{b},\ \ \vec{OC}=\vec{c}\ \ として、以下の各問に答えよ。$
$(1)\ \ \vec{c}\ を \ \vec{a},\ \ \vec{b}\ を用いて表せ。$
$(2)\ \ 内積 \ \ \vec{a}\cdot \vec{b} \ \ を求めよ。$
$(3)\ \ 内積 \ \ \vec{c}\cdot (\vec{b}- \vec{a})\ \ を求めよ。$
$(4)\ \ 三角形 \ OAB\ の面積 \ S\ を求めよ。$
(1)
$\vec{c}=\cfrac{1}{3}\vec{a}+\cfrac{2}{3}\vec{b}$
(2)
$OA=\sqrt{5},\quad OB=\sqrt{2},\quad OC=1 \quad より$
$|\vec{a}|=\sqrt{5},\quad |\vec{b}|=\sqrt{2},\quad |\vec{c}|=1$
$(1)より \quad \vec{c}=\cfrac{1}{3}\vec{a}+\cfrac{2}{3}\vec{b} \quad だから$
$3\vec{c}=\vec{a}+2\vec{b} $
$3|\vec{c}|=|\vec{a}+2\vec{b}|$
$9|\vec{c}|^2=|\vec{a}+2\vec{b}|^2$
$9|\vec{c}|^2=|\vec{a}|^2+4\vec{a} \cdot \vec{b} +4|\vec{b}|^2$
$9=5+4\vec{a} \cdot \vec{b} +4 \times 2$
$\therefore \ \ \vec{a} \cdot \vec{b}= -1$
(3)
\begin{eqnarray*} AB^2 &=&|\vec{AB}|^2\\ \\ &=&|\vec{b}-\vec{a}|^2\\ \\ &=&|\vec{b}|^2-2\vec{a} \cdot \vec{b}+|\vec{a}|^2\\ \\ &=&2-2 \times (-1) + 5\\ \\ &=&9 \end{eqnarray*} $\therefore \ \ AB=3$
$AC:CB=2:1 \quad だから \quad AC=2, \quad CB=1$
$\triangle OAC \quad において \quad OA^2=AC^2+OC^2 \quad 三平方の定理が成りたつから$
$OC \perp AC$
$よって \quad OC \perp AB \quad だから \quad \vec{OC} \perp \vec{AB}$
$\vec{OC} \cdot \vec{AB}=0$
$\therefore \vec{c} \cdot (\vec{b}-\vec{a})=0$
$(別解)$
\begin{eqnarray*} & &\vec{c} \cdot (\vec{b}-\vec{a})\\ \\ &=&\big(\cfrac{1}{3}\vec{a}+\cfrac{2}{3}\vec{b}\big) \cdot (\vec{b}-\vec{a})\\ \\ &=&\cfrac{1}{3}(\vec{a}+2\vec{b}) \cdot (\vec{b}-\vec{a})\\ \\ &=&\cfrac{1}{3}(-\vec{a} \cdot \vec{b}- |\vec{a}|^2 +2|\vec{b}|^2 )\\ \\ &=&\cfrac{1}{3}(1 - 5 + 2 \times 2 )\\ \\ &=&0 \end{eqnarray*}
$このことから \quad OC \perp AB \quad がいえる。$
(4)
\begin{eqnarray*} S &=&\cfrac{1}{2} \times AB \times OC\\ \\ &=&\cfrac{1}{2} \times 3 \times 1\\ \\ &=&\cfrac{3}{2} \end{eqnarray*}
メインメニュー に戻る