北海道大学(理系) 2025年　問題4


$a\ を正の実数とする。$
$(1)\ \ a\ が \ 1\ でないとき、複素数 \ z\ についての方程式 \ \ a|z-1|=|(a-2)z+a|\ \ を考える。この方程式を満たす$
$\quad z\ 全体の集合を複素数平面上に図示せよ。$
$(2)\ \ 方程式 \ \ |z|^2=6-a , \ \ a|z-1|=|(a-2)z+a|\ \ をともに満たす複素数 \ z\ が存在するような \ a\ の値の範囲を$
$\quad 求めよ。$

(1)


$a|z-1|=|(a-2)z+a| \ \ の両辺を平方して$

$a^2(z-1)(\overline{z}-1)=\{(a-2)z+a\}\{(a-2)\overline{z}+a\}$

$a^2(|z|^2-z-\overline{z}+1)=(a-2)^2|z|^2+a(a-2)z+a(a-2)\overline{z}+a^2$

$4a|z|^2-4|z|^2-2a^2z+2az-2a^2\overline{z} +2a\overline{z}=0$

$2(a-1)|z|^2-a(a-1)z-a(a-1)\overline{z} =0$

$a \ne 1 \quad だから \ \ 2(a-1)\ \ で割って$

　

$|z|^2-\dfrac{a}{2}z-\dfrac{a}{2}\overline{z} =0$

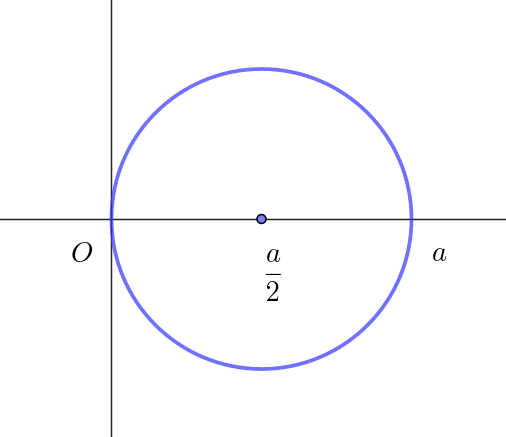
$\big(z-\dfrac{a}{2}\big)\big(\overline{z}-\dfrac{a}{2}\big)=\dfrac{a^2}{4}$

$\big|z-\dfrac{a}{2}\big|^2=\dfrac{a^2}{4}$

$\therefore \ \ \big|z-\dfrac{a}{2}\big|=\dfrac{a}{2}$

$点P(z)は、中心 \ \dfrac{a}{2},\ \ 半径 \ \dfrac{a}{2}\ \ の円を描く$

$z\ 全体の集合は右図のとおり$


$(補充)$

$a|z-1|=|(a-2)z+a| \ \ は \quad a|z-1|=|a-2||z+\dfrac{a}{a-2}|\ \ と変形すると$

$これは、2\ 定点 \ \ P(1),\ \ Q(-\dfrac{a}{a-2})\ \ からの距離の比が \ \ |a-2|:a \ \ と一定だからアポロニウスの円である。$


(2)


$|z|^2=6-a \ \ より \quad 6-a \geqq 0 \qquad 0 < a \leqq 6$

$このとき \quad |z|=\sqrt{6-a} \quad だから$

$Q(z)\ は原点中心、半径 \ \ \sqrt{6-a}\ \ の円を描く。$

$|z|^2=6-a , \quad a|z-1|=|(a-2)z+a|\ \ をともに満たす複素数 \ z\ が存在するとは$

$2\ つの円が共有点を持つことことだから$

　

$\sqrt{6-a} \leqq a$

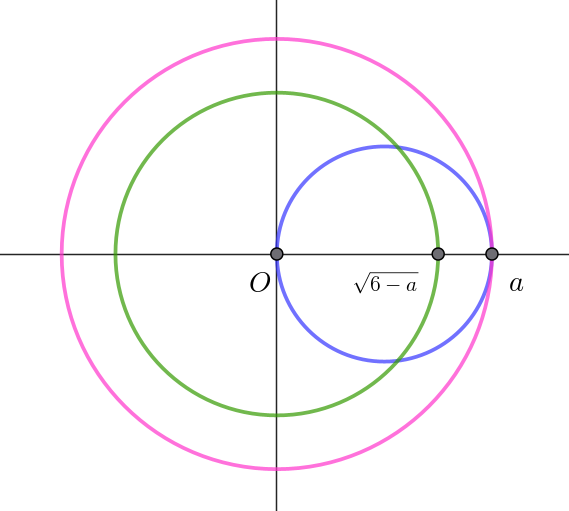
$(6-a) \leqq a^2$

$a^2+a-6 \geqq 0$

$(a-2)(a+3) \geqq 0$

$a > 0 \ \ だから \quad a \geqq 2 $

$ただし \quad 0 < a \leqq 6 \quad だから \quad 2 \leqq a \leqq 6$

$なお、a=1 \ のときは(1)の方程式を満たす \ z\ は複素数平面全体であるから、当然 \ \ |z|=\sqrt{6-a}\ \ を満たす。$

$したがって求める\ a\ の値の範囲は \quad 2 \leqq a \leqq 6,\ \ a=1$


ページの先頭へ↑



メインメニュー　に戻る