北海道大学(理系) 2025年 問題2
$円 \ C_1:x^2+y^2=1\ \ を考える。実数 \ p,\ q\ が \ \ p^2+q^2 > 1 \ \ を満たすとき、点P(p,\ q)\ から \ C_1 \ に引いた \ 2\ 本の$
$接線 \ \ell_1,\ \ \ell_2 \ の接点をそれぞれ \ Q_1(x_1,y_1),\ Q_2(x_2,\ y_2) \ とする。また、座標平面上の原点をO(0,\ 0) \ とする。$
$(1)\ \ 直線 \ \ell_1,\ \ell_2 ,\ 線分 \ OQ_1,\ OQ_2\ で囲まれた四角形の面積 \ S\ を \ p,\ q\ を用いて表せ。$
$(2)\ \ 点P\ が楕円 \ C_2: \ \dfrac{x^2}{2}+ \dfrac{y^2}{3}=1 \ \ の上を動くとき、(1)の四角形の面積 \ S\ の最大値と最小値を求めよ。$
(1)
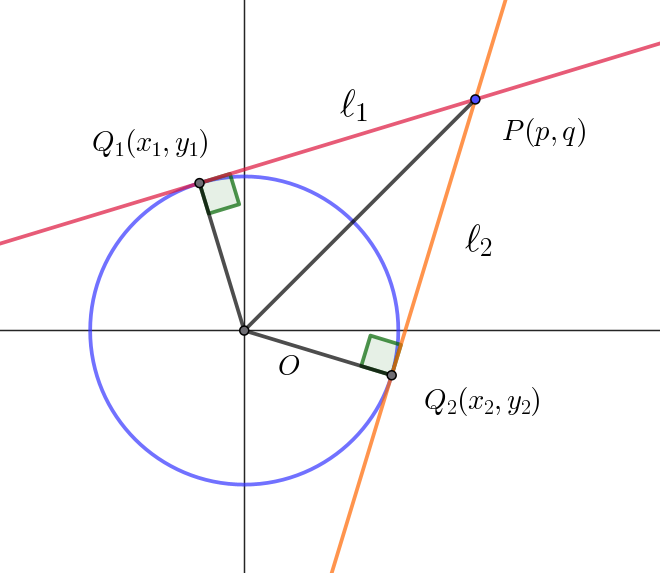
$OQ_1 \perp PQ_1,\quad OQ_2 \perp PQ_2$
$OQ_1=OQ_2$
$OP \ は共通$
$したがって \quad \triangle OPQ_1 \equiv \triangle OPQ_2 $
$PQ_1^2=OP^2-OQ_1^2=p^2+q^2-1$
$\therefore \ \ S=2\triangle OPQ_1=2 \times \dfrac{1}{2} \times OQ_1 \times P`Q_1=\sqrt{p^2+q^2-1}$
(2)
$点P\ が楕円 \ C_2: \ \dfrac{x^2}{2}+ \dfrac{y^2}{3}=1 \ \ の上を動くから$
$\dfrac{p^2}{2}+ \dfrac{q^2}{3}=1$
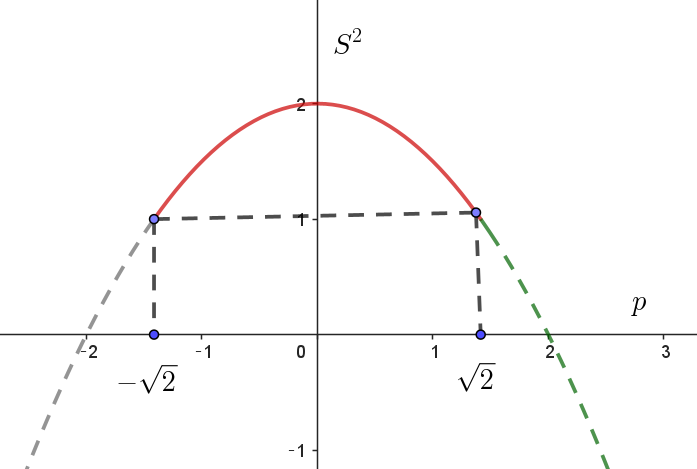
$-\sqrt{2} \leqq p \leqq \sqrt{2}$
$S^2=p^2+3(1-\dfrac{p^2}{2})-1=-\dfrac{1}{2}p^2+2$
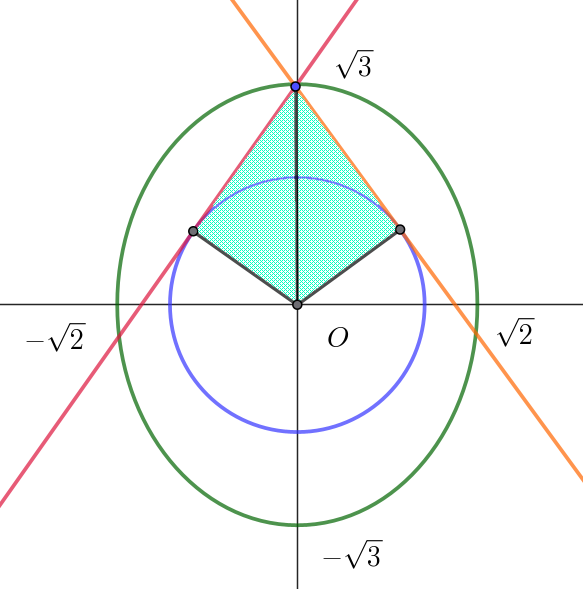
$p=0 \ \ のとき \quad q=\pm \sqrt{3}\ \ で最大値 \ \ S=\sqrt{2}$
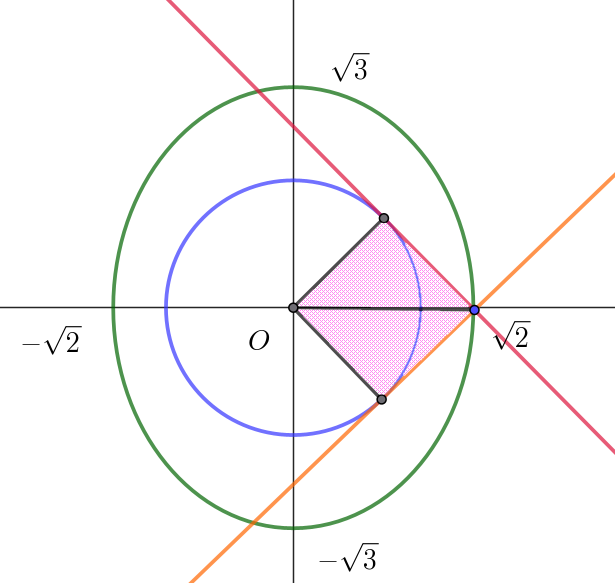
$p=\pm \sqrt{2} \ \ のとき \quad q=0 \ \ で最小値 \ \ S=1$
$\hspace{10em} 最大値 \hspace{15em} 最小値$
メインメニュー に戻る