MY MATH NOTE

北海道大学(理系) 2024年　問題5

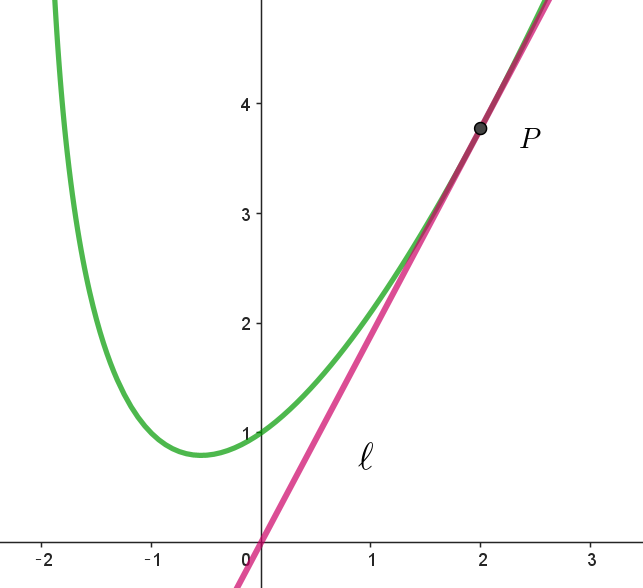
$関数 \ \ f(x)=x\log(x+2)+1 \ \ (x > -2)\ \ を考える。y=f(x)\ で表される曲線を \ C\ とする。C\ の接線のうち$
$傾きが正で原点を通るものを \ \ell \ とする。ただし、\log t \ は \ t\ の自然対数である。$
$(1)\ \ 直線 \ \ell \ の方程式を求めよ。$
$(2)\ \ 曲線 \ C\ は下に凸であることを証明せよ。$
$(3)\ \ C\ と \ \ell \ および \ y\ 軸で囲まれた部分の面積を求めよ。$

(1)

　
$f'(x)=\log (x+2)+\cfrac{x}{x+2} \quad だから$

$接点をP(a,\ f(a))\ \ (a > -2)\ \ とおくと点P\ における接線は$

$y=\big(\log (a+2)+\cfrac{a}{a+2}\big)(x-a)+a\log (a+2)+1$

$y=\big(\log (a+2)+\cfrac{a}{a+2}\big)x- \cfrac{a^2}{a+2}+1$

$原点を通るから \quad 0=- \cfrac{a^2}{a+2}+1$

$\cfrac{a^2}{a+2}=1 \qquad a^2=a+2$

$a^2-a-2=0 \qquad (a+1)(a-2)=0 \qquad \therefore \ \ a=-1,\ \ 2$

(i)$\ \ a=-1 \quad のとき$

$\quad f'(-1)=\log 1 - \cfrac{1}{-1+2}=-1 \quad 接線の傾きは負だから不適$

(ii)$\ \ a=2 \quad のとき$

$\quad f'(2)=\log 4 + \cfrac{2}{2+2}=2\log 2 + \cfrac{1}{2} \quad 接線の傾きは正だから適す$

$よって\quad \ell \ \ は \quad y=(2\log 2+\cfrac{1}{2})x $

(2)

(3)

　
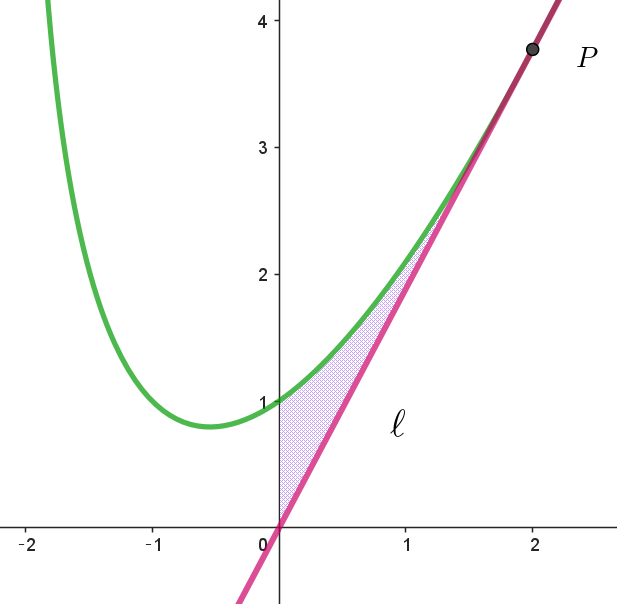
$下に凸なグラフは、曲線は接線の上側にある。$

$このことについては($曲線の凹凸$)をご覧ください。$

$求める面積 \ S\ は$
\begin{eqnarray*} S &=&\int_0^2\big\{x\log(x+2)+1-(2\log 2+\dfrac{1}{2})x\big\}dx\\ \\ &=&\big[\dfrac{x^2}{2}\log(x+2)\big]_0^2-\int_0^2\dfrac{x^2}{2} \times \dfrac{1}{x+2}dx +\big[x-(2\log 2+\dfrac{1}{2})\dfrac{x^2}{2}\big]_0^2\\ \\ &=&2\log 4 -\dfrac{1}{2}\int_0^2 \dfrac{x^2}{x+2}dx + 2-2(2\log 2+\dfrac{1}{2})\\ \\ &=&4\log 2 + 2-4\log 2-1 -\dfrac{1}{2}\int_0^2 \dfrac{x^2}{x+2}dx \\ \\ &=&1 -\dfrac{1}{2}\int_0^2 \dfrac{x^2-4+4}{x+2}dx \\ \\ &=&1 -\dfrac{1}{2}\int_0^2 \big(x-2+\dfrac{4}{x+2}\big)dx \\ \\ &=&1 -\dfrac{1}{2}\big[\dfrac{x^2}{2}-2x+4\log(x+2)\big]_0^2\\ \\ &=&1 -\dfrac{1}{2}(2-4+4\log 4 -4\log 2)\\ \\ &=&2(1-\log 2) \end{eqnarray*}

ページの先頭へ↑