MY MATH NOTE

北海道大学(理系) 2024年　問題4

$三角形 \ OAB\ が \ |\vec{OA}|=3,\ \ |\vec{AB}|=5,\ \ \vec{OA}\cdot \vec{OB}=10\ \ をみたしているとする。三角形 \ OAB\ の内接円の$
$中心を \ I\ とし、この内接円と辺 \ OA\ の接点を \ H\ とする。$
$(1)\ \ 辺 \ OB\ の長さを求めよ。$
$(2)\ \ \vec{OI}\ を \ \vec{OA}\ と \ \vec{OB}\ を用いて表せ。$
$(3)\ \ \vec{HI}\ を \ \vec{OA}\ と \ \vec{OB}\ を用いて表せ。$

(1)

　
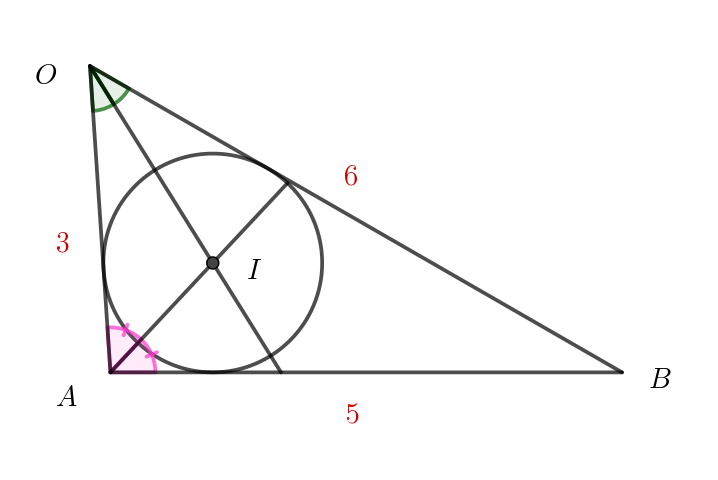
$\vec{OA}\cdot \vec{OB}=10\ \ より \quad |\vec{OA}||\vec{OB}|\cos \angle AOB =10$

$3 \times OB \times \cos \angle AOB =10$

$\triangle OABに余弦定理を用いて$

\begin{eqnarray*} \cos \angle AOB &=&\cfrac{OA^2+OB^2-AB^2}{2OA \cdot OB}\\ \\ &=&\cfrac{9+OB^2-25}{2\times 3 \times OB}\\ \\ &=&\cfrac{OB^2-16}{6OB}\\ \end{eqnarray*} $これを上式に代入して$

$3 \times OB \times \cfrac{OB^2-16}{6OB}=10$

$OB^2-16=20$

$\therefore \ \ OB=6$

(2)

　
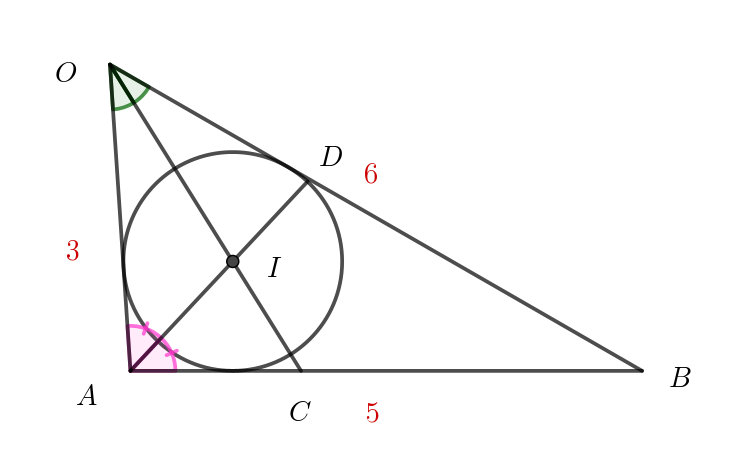
$OI\ の延長と辺 \ AB\ の交点を \ C,$

$AI\ の延長と辺 \ OB\ の交点を \ D\ とする。$

$\triangle OAB \ \ において$

$OA:OB=AC:CB \quad だから \quad AC:CB=3:6=1:2$

$\vec{OC}=\cfrac{2\vec{OA}+\vec{OB}}{1+2}=\cfrac{2}{3}\vec{a}+\cfrac{1}{3}\vec{b}$

$AB=5 \quad だから \quad AC=5 \times \cfrac{1}{3}=\cfrac{5}{3}$

$\triangle ACO \ \ において$

$AO:AC=OI:IC \quad だから \quad OI:IC=3:\dfrac{5}{3}=9:5$

$\vec{OI}=\cfrac{9}{14}\vec{OC}=\cfrac{9}{14}\big(\cfrac{2}{3}\vec{a}+\cfrac{1}{3}\vec{b}\big)=\cfrac{3}{7}\vec{a}+\cfrac{3}{14}\vec{b}$

(3)

　
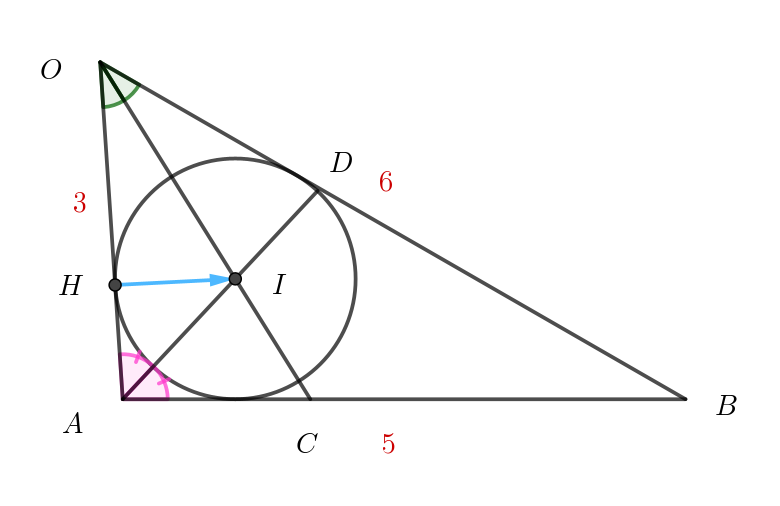
$\vec{OH}=m\vec{OA}=m\vec{a} \quad とおく$

$OA \perp HI \quad だから \quad \vec{OA} \cdot \vec{HI}=0$

$\vec{OA} \cdot (\vec{OI}- \vec{OH})=0$

$\vec{a} \cdot \big((\cfrac{3}{7}\vec{a}+\cfrac{3}{14}\vec{b}) -m\vec{a}\big)=0$

$\vec{a} \cdot \big((\cfrac{3}{7}-m)\vec{a}+\cfrac{3}{14}\vec{b}\big)=0$

$(\cfrac{3}{7}-m)|\vec{a}|^2 + \cfrac{3}{14}\vec{a} \cdot \vec{b}=0$

$9(\cfrac{3}{7}-m) + \cfrac{3}{14} \times 10 =0$

$m=\cfrac{2}{3} \qquad \therefore \ \ \vec{OH}=\cfrac{2}{3}\vec{a} $

$\vec{HI}=\vec{OI}-\vec{OH}=\big(\cfrac{3}{7}\vec{a}+\cfrac{3}{14}\vec{b}\big)-\cfrac{2}{3}\vec{a}=-\cfrac{5}{21}\vec{a}+\cfrac{3}{14}\vec{b}$


$(別解)$

　
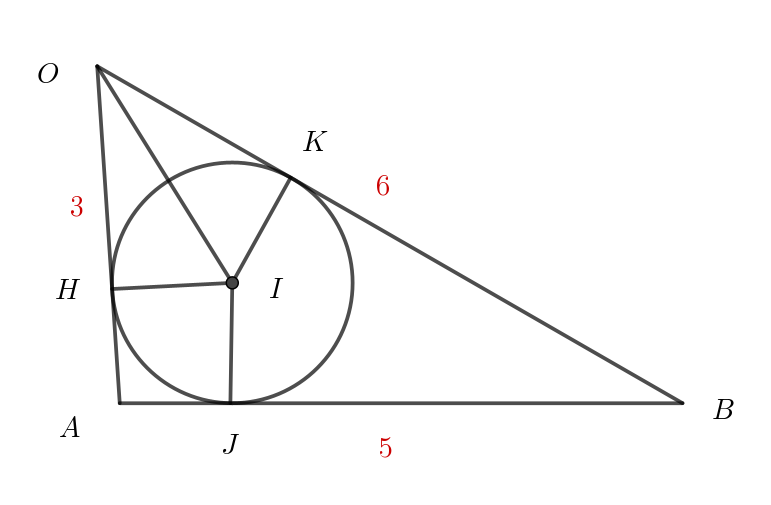
$辺 \ AB,\ \ OB\ と内接円の接点をそれぞれ点 \ J,\ K\ とおく。$

$\triangle OHI \ \ と \ \ \triangle OKI \quad において$

$\angle OHI=\angle OKI=90°$

$このことについては($円の接線$)をご覧ください。$

$OI\ は共通で、\angle HOI=\angle KOI$

$よって \quad \triangle OHI \equiv \triangle OKI $

$したがって \quad OH=OK$

$同様にして \quad AH=AJ, \quad BJ=BK $

$OH=l,\ \ AH=m.\ \ BJ=n \quad とおくと$

$l+m=OA=3 \hspace{5em}①$

$m+n=AB=5 \hspace{5em}②$

$n+l=OB=6 \hspace{5em}③$

$辺々加えて \quad 2(l+m+n)=14$

$l+m+n=7 \hspace{5em}④$

$④-②\ \ より \quad l=2$

ページの先頭へ↑