北海道大学(理系) 2024年 問題2
$各面に \ 1\ つずつ数が書かれた正八面体のさいころがある。「1」,「2」,「3」が書かれた面がそれぞれ \ 1\ つ$
$ずつあり、残りの \ 5\ つの面には「0」が書かれている。このさいころを水平な床面に投げて、出た面に$
$書かれた数を持ち点に加えるという試行を考える。最初の持ち点は \ 0\ とし、この試行を繰り返す。例えば、$
$3\ 回の試行を行ったとき、出た面に書かれた数が「0」,「2」,「3」であれば、持ち点は \ 5\ となる。なお、$
$さいころが水平な床面にあるとき、さいころの上部の水平な面を出た面とよぶ。また、さいころを投げる$
$とき、各面が出ることは同様に確からしいとする。$
$(1)\ \ この試行を \ n\ 回行ったとき、持ち点が \ 2\ 以下である確率を求めよ。ただし、n\ は \ 2\ 以上の自然数とする。$
$(2)\ \ この試行を \ 4\ 回行って持ち点が \ 10\ 以上であったときに、さらにこの試行を \ 2\ 回行って持ち点が \ 17\ 以上$
$\quad である条件付き確率を求めよ。$
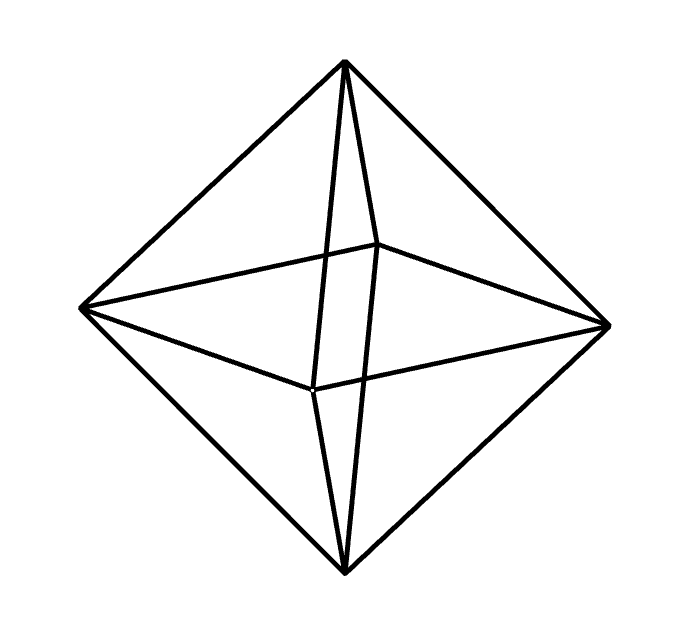
$正八面体は通常左側の図のように表示されますので、これを水平な床面に投げて、上部の水平な面を$
$出た面にするイメージがわきにくいですが、これが右側の図です。$

(1)
$n\ 回の試行での持ち点を \ S\ とする。S が \ 2\ 以下であるのは$
(i)$\ \ S=0\ \ のとき$
$\quad 0\ が \ n\ 回出ることだから、その確率は \quad p_1=\big(\cfrac{5}{8}\big)^n$
(ii)$\ \ S=1\ \ のとき$
$\quad 1\ が \ 1回、0\ が \ (n-1)\ 回出ることだから、その確率は \quad p_2={}_nC_1\big(\cfrac{1}{8}\big)\big(\cfrac{5}{8}\big)^{n-1}$
(iii)$\ \ S=2 \ \ のとき$
$\quad 1\ が \ 2\ 回、0\ が \ (n-2)\ 回出るか、または \ 2\ が \ 1\ 回、0\ が \ (n-1)\ 回が出ることで、これらは互いに排反だから、$
$\quad その確率は \quad p_3={}_nC_2\big(\cfrac{1}{8}\big)^2\big(\cfrac{5}{8}\big)^{n-2}+ {}_nC_1\big(\cfrac{1}{8}\big)\big(\cfrac{5}{8}\big)^{n-1}$
(i),(ii),(iii)$\ \ は互いに排反だから求める確率 \ P\ は$
\begin{eqnarray*} P &=&p_1+p_2+p_3\\ \\ &=&\big(\cfrac{5}{8}\big)^n + {}_nC_1\big(\cfrac{1}{8}\big)\big(\cfrac{5}{8}\big)^{n-1}+ {}_nC_2\big(\cfrac{1}{8}\big)^2\big(\cfrac{5}{8}\big)^{n-2}+ {}_nC_1\big(\cfrac{1}{8}\big)\big(\cfrac{5}{8}\big)^{n-1}\\ \\ &=&\big(5^2+5n+\dfrac{n(n-1)}{2}+5n \big) \times \cfrac{5^{n-2}}{8^n}\\ \\ &=&\cfrac{1}{2}(n^2+19n+50) \times \cfrac{5^{n-2}}{8^n}\\ \\ &=&\cfrac{1}{128}(n^2+19n+50) \big(\cfrac{5}{8}\big)^{n-2}\\ \end{eqnarray*}
(2)
$4\ 回行って持ち点が \ 10\ 以上である事象をA、さらにこの試行を \ 2\ 回行って持ち点が \ 17\ 以上である事象をBとする。$
$事象 \ A\ は次の \ 4\ 通りの場合がある。$
(i)$\ \ \{3,\ 3,\ 3,\ 3\}\ \ の数字が出る場合で、この確率は \quad \big(\cfrac{1}{8}\big)^4 \quad で、持ち点は \ 12\ 点$
(ii)$\ \ \{3,\ 3,\ 3,\ 2\}\ \ の数字が出る場合で、この確率は \quad {}_4C_1\big(\cfrac{1}{8}\big)^4 \quad で、持ち点は \ 11\ 点$
(iii)$\ \ \{3,\ 3,\ 3,\ 1\}\ \ の数字が出る場合で、この確率は \quad {}_4C_1\big(\cfrac{1}{8}\big)^4 \quad で、持ち点は \ 10\ 点$
(iv)$\ \ \{3,\ 3,\ 2,\ 2\}\ \ の数字が出る場合で、この確率は \quad {}_4C_2\big(\cfrac{1}{8}\big)^4 \quad で、持ち点は \ 10\ 点$
$これらは互いに排反だから$
$P(A)=\big(\cfrac{1}{8}\big)^4 + {}_4C_1\big(\cfrac{1}{8}\big)^4 + {}_4C_1\big(\cfrac{1}{8}\big)^4 + {}_4C_2\big(\cfrac{1}{8}\big)^4=\cfrac{15}{8^4} $
$事象 \ \ A \cap B \ \ は次の \ 3\ 通りの場合がある。$
(i)$\ \ \{3,\ 3,\ 3,\ 3\} \ \ \{3,\ 3\}\ \ の数字が出る場合で、この確率は \quad \big(\cfrac{1}{8}\big)^6 \quad で、持ち点は \ 18\ 点$
(ii)$\ \ \{3,\ 3,\ 3,\ 3\} \ \ \{3,\ 2\}\ \ の数字が出る場合で、この確率は \quad {}_2C1\big(\cfrac{1}{8}\big)^6 \quad で、持ち点は \ 17\ 点$
(iii)$\ \ \{3,\ 3,\ 3,\ 2\} \ \ \{3,\ 3\}\ \ の数字が出る場合で、この確率は \quad {}_4C1\big(\cfrac{1}{8}\big)^6 \quad で、持ち点は \ 17\ 点$
$これらは互いに排反だから$
$P(A \cap B)=\big(\cfrac{1}{8}\big)^6 + {}_2C_1\big(\cfrac{1}{8}\big)^6 + {}_4C_1\big(\cfrac{1}{8}\big)^6 =\cfrac{7}{8^6} $
$したがって、事象 \ A\ が起こったときに、事象 \ B\ が起こる条件付き確率は$
$P_A(B)=\cfrac{P(A \cap B)}{P(A)}=\cfrac{7}{8^6} \times \cfrac{8^4}{15}=\cfrac{7}{15 \times 8^2}=\cfrac{7}{960}$
メインメニュー に戻る