北海道大学(理系) 2024年 問題1
$t\ を実数とし、xy\ 平面上の点P(\cos 2t,\ \cos t) \ \ および点Q(\sin t,\ \sin 2t)\ \ を考える。$
$(1)\ \ 点P\ と点Q\ が一致するような \ t\ の値をすべて求めよ。$
$(2)\ \ t\ が \ \ 0 < t < 2\pi \ \ の範囲で変化するとき、点P\ の軌跡を \ xy\ 平面上に図示せよ。ただし、x\ 軸、y\ 軸との$
$\quad 共有点がある場合は、それらの座標を求め、図中に示せ。$
(1)
$点P\ と点Q\ が一致するような \ t\ の値は次の連立方程式の解である。$
\[ \left\{ \begin{array}{l} \cos 2t =\sin t \hspace{5em} ①\\ \cos t=\sin 2t \hspace{5em} ②\\ \end{array} \right. \]
$①より \quad 1-2\sin ^2t=\sin t$
$2\sin ^2t +\sin t-1=0$
$(2\sin t-1)(\sin t+1)=0$
$\sin t=\cfrac{1}{2},\ \ -1$
$②より \quad \cos t=2\sin t\cos t$
$\cos t(2\sin t-1)=0$
$\cos t=0,\quad \sin t=\cfrac{1}{2}$
(i)$\ \ \sin t=\cfrac{1}{2}\ \ は \ ①\ ②\ を満たすから解である。$
$\quad これを解いて \quad t=\cfrac{\pi}{6}+2n\pi,\quad \cfrac{5}{6}\pi+2n\pi$
(ii)$\ \ \sin t=-1 \quad かつ \quad \cos t=0 \ \ は \ ①\ ②\ を満たすから解である。$
$\quad これを解いて \quad t=\cfrac{3}{2}+2n\pi$
(i),(ii)$\ \ より\ \ 点P\ と点Q\ が一致するような \ t\ の値は$
$t=\cfrac{\pi}{6}+2n\pi,\quad \cfrac{5}{6}\pi+2n\pi,\quad \cfrac{3}{2}+2n\pi \ \ (n\ は任意の整数)$
$(注意)$
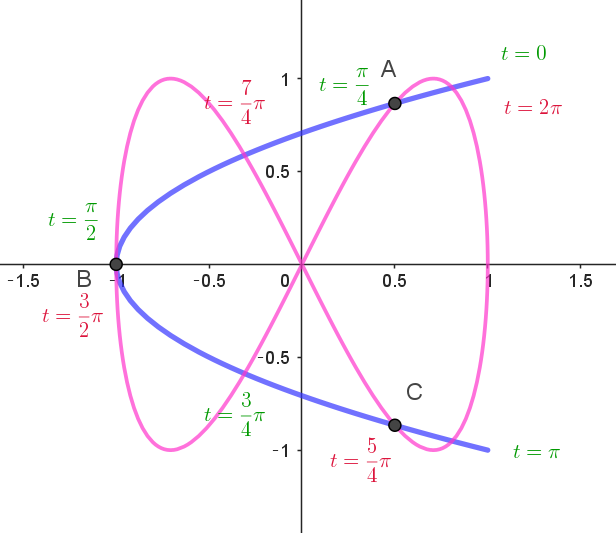
$次の(2)に関連しますが、点Pと点Qの描く軌跡は右図のようになり、交点は7個あります。$
$そのうち点A,B,C の3個だけが同一のtの値による交点です。$
(2)
$x=\cos 2t , \quad y=\cos t \quad とおくと$
$x=2\cos ^2t -1 \quad だから$
$x=2y^2-1$
$x\ 軸との交点は \ \ y=0 \ \ とおいて \quad x=-1$
$このとき \ \ \cos t=0 \ \ より \quad t=\cfrac{\pi}{2}, \quad \cfrac{3}{2}\pi$
$y\ 軸との交点は \ \ x=0 \ \ とおいて \quad y^2=\cfrac{1}{2} \qquad y=\pm \cfrac{1}{\sqrt{2}}$
$このとき \ \ \cos 2t=0 \ \ より \ \ 0 < 2t < 4\pi \ \ だから$
$2t=\cfrac{\pi}{2},\quad \cfrac{3}{2}\pi, \quad \cfrac{5}{2}\pi,\quad \cfrac{7}{2}\pi$
$したがって \quad t=\cfrac{\pi}{4},\quad \cfrac{3}{4}\pi, \quad \cfrac{5}{4}\pi,\quad \cfrac{7}{4}\pi$
$ただし$
$t=\cfrac{\pi}{4},\ \ \cfrac{7}{4}\pi \quad のときは \quad y=\cfrac{1}{\sqrt{2}}$
$t=\cfrac{3}{4}\pi,\ \ \cfrac{5}{4}\pi \quad のときは \quad y=-\cfrac{1}{\sqrt{2}}$
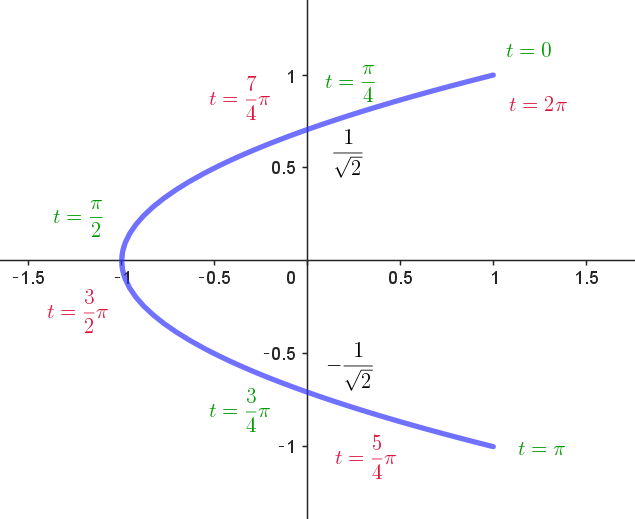
$グラフは右図のような放物線で、\pi < t < 2\pi \ \ では、0 < t < \pi \ \ の軌跡を逆方向にたどる。$
$(補充)$
$(1)の注意で示しましたが、点Q\ の軌跡について考えてみましょう。$
$x=\sin t,\quad y=\sin 2t=2\sin t \cos t =2x\cos t$
$(2x\sin t)^2+(2x\cos t)^2=(2x^2)^2+y^2$
$4x^2=4x^4+y^2$
$y^2=4x^2(1-x^2)$
$x \geqq 0,\ \ y \geqq 0 \ \ で \ \ y=2x\sqrt{1-x^2}$
$このグラフは増減を調べることによって描くことができますが、さらに \ x\ 軸、y\ 軸に関して対称にかきます。$
$(1)で描いたピンク色のグラフになります。$
$一般に \quad x=\sin at,\ \ y=\sin bt \ \ (a,\ b\ は正の整数)\ \ の表すグラフを「リサージュ図形」といいます。$
$\hspace{5em} a=1,\ \ b=3 \hspace{12em}a=2,\ \ b=3 \hspace{12em}a=3,\ \ b=4$
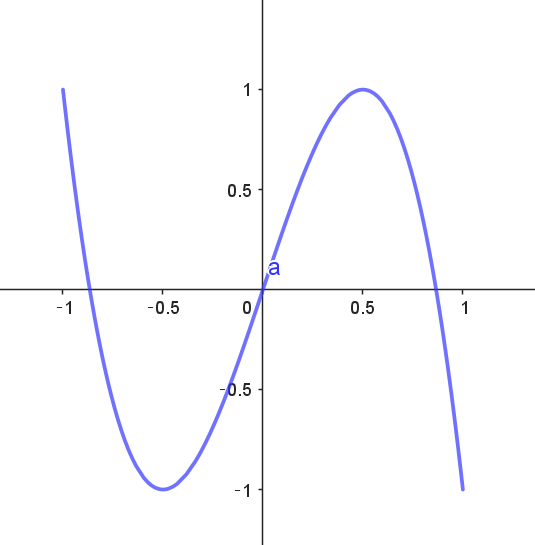
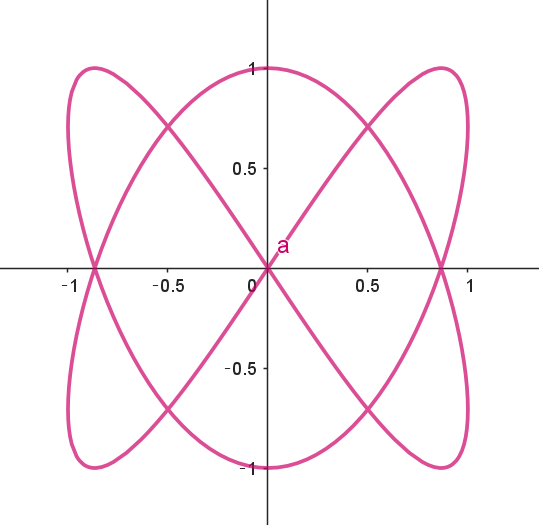
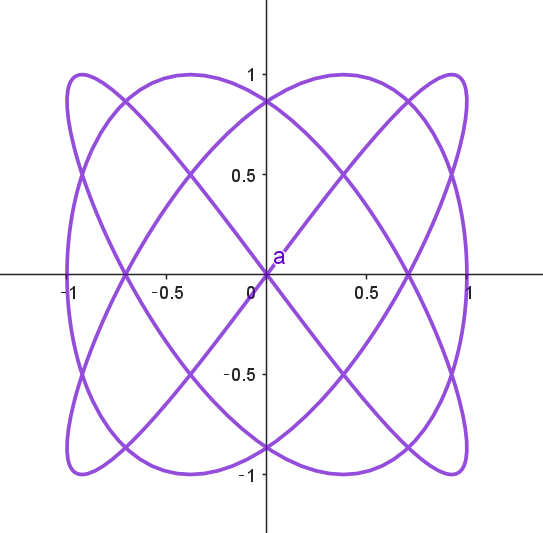
$a=1,\ \ b=3\ \ は \ 3\ 次関数のグラフですが、一般の \ a,\ b\ について、x,\ y\ 表示は困難です。$
メインメニュー に戻る