北海道大学(理系) 2018年 問題3
$数字の \ 2\ が書かれたカードが \ 2\ 枚、同様に、数字の \ 0,\ 1,\ 8\ が書かれたカードがそれぞれ \ 2\ 枚、$
$あわせて \ 8\ 枚のカードがある。これから \ 4\ 枚を取り出し、横一列に並べてできる自然数を \ n\ とする。$
$ただし、0\ のカードが左から \ 1\ 枚または \ 2\ 枚現れる場合は、n\ は \ 3\ 桁または \ 2\ 桁の自然数と$
$それぞれ考える。例えば、左から順に \ 0,\ 0,\ 1,\ 1\ の数字のカードが並ぶ場合の \ n\ は \ 11\ である。$
$(1)\ \ a,\ b,\ c,\ d\ は整数とする。1000a+100b+10c+d\ \ が \ 9\ の倍数となることと \ a+b+c+d\ が$
$\quad 9\ の倍数になることは同値であることを示せ。$
$(2)\ \ n\ が \ 9\ の倍数である確率を求めよ。$
$(3)\ \ n\ が偶数であったとき、n\ が \ 9\ の倍数である確率を求めよ。$
$(解説)$
$(1)\ \ どの教科書にも載っている整数論の基本事項です。$
$(2)\ \ 4\ つの数字の和が \ 9\ または \ 18\ になる組合せを探します。$
$(3)\ \ n\ が偶数である事象の余事象である \ n\ が奇数となる確率を求めた方が簡単です。$
(1)
$N=1000a+100b+10c+d=9(111a+11b+c)+a+b+c+d$
$\quad 111a+11b+c=k\ \ (kは整数)\ \ とおくと \qquad N=9k+a+b+c+d$
(i)$\ \ N\ が \ 9\ の倍数ならば \quad N=9l \ \ (lは整数)とおけるから$
$\qquad 9l=9k+a+b+c+d \qquad $
$\qquad \therefore \ \ a+b+c+d=9(l-k) \quad となって \quad a+b+c+d \ \ は \ 9\ の倍数$
(ii)$\ \ a+b+c+d \ \ が \ 9\ の倍数ならば \quad a+b+c+d=9m \ \ (mは整数)とおけるから$
$\qquad N=9k+9m=9(k+m) \quad となって \quad N\ は \ 9\ の倍数$
(i),(ii)$より、1000a+100b+10c+d \ \ が \ 9\ の倍数となることと \ \ a+b+c+d\ が \ 9\ の倍数になることは$
$同値である。$
(2)
$(1)より \ n\ が \ 9\ の倍数である事象は、a+b+c+d\ \ が \ 9\ の倍数である事象と同じである。$
$a+b+c+d \ \ が \ 9\ の倍数となる事象は$
(i)$\ \ \{0,\ 0,\ 1,\ 8\}\ の数字の組合せのカードが出た場合$
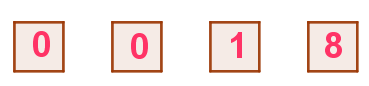 $\qquad 1\ と \ 8\ のカードの取り出し方はそれぞれ \ 2\ 通りあり、数字の並び方は$
$\qquad 1\ と \ 8\ のカードの取り出し方はそれぞれ \ 2\ 通りあり、数字の並び方は$
$\hspace{3em} \ 4!\ 通りだから$
$\hspace{15em} 2 \times 2 \times 4! \ \ 通り$
(ii)$\ \ \{0,\ 2,\ 8,\ 8\}\ の数字の組合せのカードが出た場合$
 $\qquad 0\ と \ 2\ のカードの取り出し方はそれぞれ \ 2\ 通りあり、数字の並び方は$
$\qquad 0\ と \ 2\ のカードの取り出し方はそれぞれ \ 2\ 通りあり、数字の並び方は$
$\hspace{3em} \ 4!\ 通りだから$
$\hspace{15em} 2 \times 2 \times 4! \ \ 通り$
(iii)$\ \ \{1,\ 1,\ 8,\ 8\}\ の数字の組合せのカードが出た場合$
 $\qquad 数字の並び方は \ 4!\ \ 通り$
$\qquad 数字の並び方は \ 4!\ \ 通り$
$よって全部で \quad 2 \times 2 \times 4!+ 2 \times 2 \times 4!+4!=9 \times 4! \ \ 通り$
$すべてのカードの出し方、すなわち \ n\ の個数は \quad _8P_4 \ \ 通りだから求める確率は$
$\qquad P=\cfrac{9 \times 4!}{_8P_4 }=\cfrac{9 \times 4!}{8 \times 7 \times 6 \times 5}=\cfrac{9}{70}$
(3)
$n\ が偶数である事象を \ E\ とすると、その余事象 \ \overline{E}\ は奇数である。$
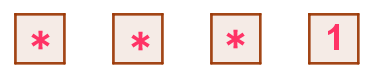 $\qquad 奇数となるのは \ 1\ 桁目が \ 1\ の場合で、残りはどの数字でもよい。$
$\qquad 奇数となるのは \ 1\ 桁目が \ 1\ の場合で、残りはどの数字でもよい。$
$\qquad 1\ のカードの取り出し方は \ 2\ 通りあり、他の数字の並び方は \ \ _7P_3 \ \ 通りだから$
$\hspace{3em} P(\overline{E})=\cfrac{_7P_3 \times 2 }{_8P_4}=\cfrac{7 \times 6 \times 5 \times 2}{8 \times 7 \times 6 \times 5}=\cfrac{1}{4}$
$よって P(E)=1-P(\overline{E})=1-\cfrac{1}{4}=\cfrac{3}{4}$
$偶数かつ \ 9\ の倍数となる事象は$
(i)$\ \ \{0,0,1,8\}\ の数字の組合せのカードが出た場合$
 $\qquad 1\ 桁目の0が \ 2\ 通り、1\ と \ 8\ のカードの取り出し方はそれぞれ \ 2\ 通りあり、$
$\qquad 1\ 桁目の0が \ 2\ 通り、1\ と \ 8\ のカードの取り出し方はそれぞれ \ 2\ 通りあり、$
$\hspace{3em} 数字の並び方は \ 3!\ \ 通りだから$
$\hspace{15em} 2 \times 2 \times 2 \times 3! \ \ 通り$
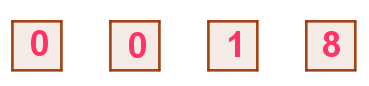 $\qquad 1\ 桁目の \ 8\ が \ 2\ 通り、1\ のカードの取り出し方は \ 2\ 通りあり、数字の並び方は$
$\qquad 1\ 桁目の \ 8\ が \ 2\ 通り、1\ のカードの取り出し方は \ 2\ 通りあり、数字の並び方は$
$\hspace{3em} 3!\ \ 通りだから$
$\hspace{15em} 2 \times 2 \times 3! \ \ 通り$
(ii)$\ \ \{0,\ 2,\ 8,\ 8\}\ の数字の組合せのカードが出た場合$
 $\qquad 0,\ 2,\ 8\ は偶数であるからどの数字が \ 1\ 桁目にきてもよい。0\ と \ 2\ のカードの$
$\qquad 0,\ 2,\ 8\ は偶数であるからどの数字が \ 1\ 桁目にきてもよい。0\ と \ 2\ のカードの$
$\hspace{3em} 取り出し方はそれぞれ \ 2\ 通りあり、数字の並び方は \ 4!\ 通りだから$
$\hspace{15em} 2 \times 2 \times 4! \ \ 通り$
(iii)$\ \ \{1,\ 1,\ 8,\ 8\}\ の数字の組合せのカードが出た場合$
 $\qquad 1\ 桁目の \ 8\ が \ 2\ 通り、数字の並び方は \ 3!\ 通りだから$
$\qquad 1\ 桁目の \ 8\ が \ 2\ 通り、数字の並び方は \ 3!\ 通りだから$
$\hspace{5em} 2 \times 3! \ \ 通り$
$よって全部で \qquad 2 \times 2 \times 2 \times 3!+ 2 \times 2 \times 3!+ 2 \times 2 \times 4!+ 2 \times 3!=2 \times 3! \times (4+2+8+1)=2 \times 3! \times 15 \ \ 通り$
$すべてのカードの出し方、すなわち \ n\ の個数は \quad _8P_4 \ \ 通りだから$
$n\ が \ 9\ の倍数である事象を \ A\ とすると、n\ が偶数かつ \ 9\ の倍数である確率は$
$\qquad P(E \cap A)=\cfrac{2 \times 3! \times 15}{_8P_4 }=\cfrac{2 \times 3! \times 15 }{8 \times 7 \times 6 \times 5}=\cfrac{3}{28}$
$したがって、n\ が偶数であったとき、n\ が \ 9\ の倍数である条件付き確率 \ P_E(A)\ は$
$\qquad P_E(A)=\cfrac{P(E \cap A)}{P(E)}=\cfrac{3}{28} \times \cfrac{4}{3}=\cfrac{1}{7}$
メインメニュー に戻る