北海道大学(理系) 2018年 問題2
$z+\cfrac{4}{z}\ が実数となるような \ 0\ と異なる複素数 \ z\ の全体をDとする。$
$(1)\ \ Dを複素数平面上に図示せよ。$
$(2)\ \ k\ を実数とする。Dに属する \ z\ で方程式 \ \ k(z+\cfrac{4}{z}+8)=i(z-\cfrac{4}{z})\ \ を満たすものが存在するような$
$\quad k\ の値の範囲を求めよ。ただし、i\ は虚数単位を表す。$
$(解説)$
$(1)は複素数で与えられた式が実数となる関係式を導き、グラフをかく問題です。$
$(2)は \ z\ を極形式で表し、偏角の問題として処理すればよい。4パターンの解答を示します。$
(1)
$実数となる条件は \quad z+\cfrac{4}{z}=\overline{z+\cfrac{4}{z}} \quad だから$
$z+\cfrac{4}{z}=\overline{z}+\cfrac{4}{\overline{z}} \hspace{8em} z-\overline{z}+4(\cfrac{1}{z}-\cfrac{1}{\overline{z}})=0$
$z\overline{z}(z-\overline{z})+4(\overline{z}-z)=0 \hspace{5em} (z-\overline{z})(z\overline{z}-4)=0$
$z=\overline{z},\quad z\overline{z}=4$
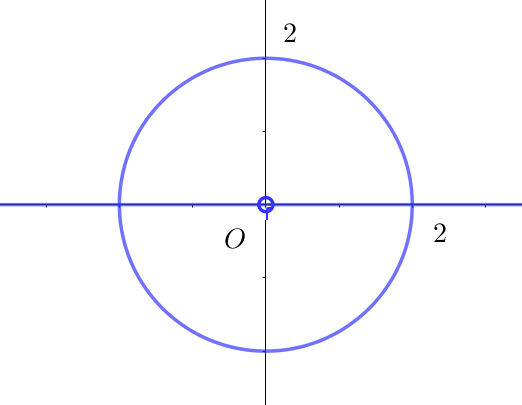
(i)$\ \ z=\overline{z} \ \ のとき \ \ z\ は実数 \ \ (ただし \ \ z \ne 0)$
(ii)$\ \ z\overline{z}=4 \ \ のとき $
$\qquad |z|^2=4 \quad より \quad |z|=2 \quad これは原点中心、半径 \ 2\ の円を表す。$
$Dは右図のとおり$
(2)
(i)$\ \ zが実数 のとき \quad z=x \quad (ただし \ \ x \ne 0 \ は実数)$
$\quad k(x+\cfrac{4}{x}+8)=i(x-\cfrac{4}{x}) \qquad 左辺は実数だから \quad x-\cfrac{4}{x}=0$
$\quad x^2=4 \quad より \quad x=\pm 2$
$\quad このとき左辺は$
$\qquad x=2 \ \ のとき \quad 12k=0 \qquad k=0$
$\qquad x=-2 \ \ のとき \quad 4k=0 \qquad k=0$
$\quad よって \quad k=0$
(ii)$\ \ |z|=2 \quad のとき $
$\quad z=2(\cos \theta +i\sin \theta) \ \ とおくと \quad \cfrac{1}{z}=\cfrac{1}{2}(\cos \theta -\sin \theta)$
$\quad k\{2(\cos \theta +i\sin \theta)+2(\cos \theta -i\sin \theta)+8\}=i\{2(\cos \theta +i\sin \theta) -2(\cos \theta -i\sin \theta)\}$
$\quad k(4\cos \theta +8)=i \times 4i\sin \theta$
$\quad k(\cos \theta + 2)=-\sin \theta$
$\quad \sin \theta + k\cos \theta =-2k$
$これを満たす\theta が存在するためのkの値の範囲を、次の \ 4\ 通りの方法で示しますが、$
$ここからはもう複素数の話ではなく、実数の領域になります。$
$解法1 \quad (三角関数の合成)$
$\quad \sin \theta + k\cos \theta =-2k \quad より$
$\quad \sqrt{1+k^2}\sin (\theta + \alpha )=-2k \quad ただし \quad \cos \alpha =\cfrac{1}{\sqrt{1+k^2}},\quad \sin \alpha =\cfrac{k}{\sqrt{1+k^2}}$
$\quad \sin (\theta + \alpha )=-\cfrac{2k}{\sqrt{1+k^2}} \quad より \quad |\cfrac{2k}{\sqrt{1+k^2}}| \leqq 1$
$\quad |2k| \leqq |\sqrt{1+k^2}| \quad 両辺平方して \quad 4k^2 \leqq 1+k^2$
$\quad k^2 \leqq \cfrac{1}{3} \qquad \therefore -\cfrac{1}{\sqrt{3}} \leqq k \leqq \cfrac{1}{\sqrt{3}}$
$\quad この範囲には \ k=0 \ が含まれている。$
$解法2 \quad (2次方程式の解の存在範囲)$
$\quad \sin \theta + k\cos \theta =-2k \quad より \quad \sin \theta =- k(2+\cos \theta)$
$\quad \sin ^2\theta +\cos ^2\theta =1 \quad に代入して \qquad k^2(2+\cos \theta)^2+\cos ^2\theta =1$
$\quad (k^2+1)\cos ^2\theta +4k^2\cos \theta +4k^2-1=0 \qquad \cos \theta =t \quad とおくと \quad (k^2+1)t^2 +4k^2t +4k^2-1=0$
$\quad これが \ \ [-1,\ 1]\ \ で実数解をもつ条件は$
(i)$\ \ 実数解をもつから$
$\quad \cfrac{D}{4}=(2k^2)^2-(k^2+1)(4k^2-1) \geqq 0$
$\quad 3k^2-1 \leqq 0 \qquad \therefore -\cfrac{1}{\sqrt{3}} \leqq k \leqq \cfrac{1}{\sqrt{3}}$
$\quad f(t)=(k^2+1)t^2 +4k^2t +4k^2-1 \quad とおくと$
(ii)$\ \ f(1) \geqq 0 \quad より$
$\quad (k^2+1)+4k^2+4k^2-1 \geqq 0 \qquad 9k^2 \geqq 0 \quad となり、すべての実数 \ k\ で成りたつ$
(iii)$\ \ f(-1) \geqq 0 \quad より$
$\quad (k^2+1)-4k^2+4k^2-1 \geqq 0 \qquad k^2 \geqq 0 \quad となり、すべての実数\ k\ で成りたつ$
(iv)$\ \ 軸について $
$\quad -1 < -\cfrac{2k^2}{k^2+1} < 1$
$\quad 左側の不等号 \quad k^2+1 > 2k^2 \quad より \qquad k^2< 1 \qquad \therefore -1 < k < 1$
$\quad 右側の不等号 \quad -2k^2 < k^2+1 \quad より \quad 3k^2+1 > 0 \qquad すべての実数 \ k\ で成りたつ$
(i)~(iv)$\ \ より \qquad -\cfrac{1}{\sqrt{3}} \leqq k \leqq \cfrac{1}{\sqrt{3}}$
$また$
$\quad \sin \theta + k\cos \theta =-2k \quad より \quad k=-\cfrac{\sin \theta}{2+\cos \theta} \quad と解くと$
$\quad f(\theta)=-\cfrac{\sin \theta}{2+\cos \theta} \quad の最大値と最小値を求めることから \ k\ の範囲を求めることができる。$
$\quad この方法には、微分法でグラフをかく方法と図形的に求める方法がある。$
$解法3 \quad (グラフをかく方法)$
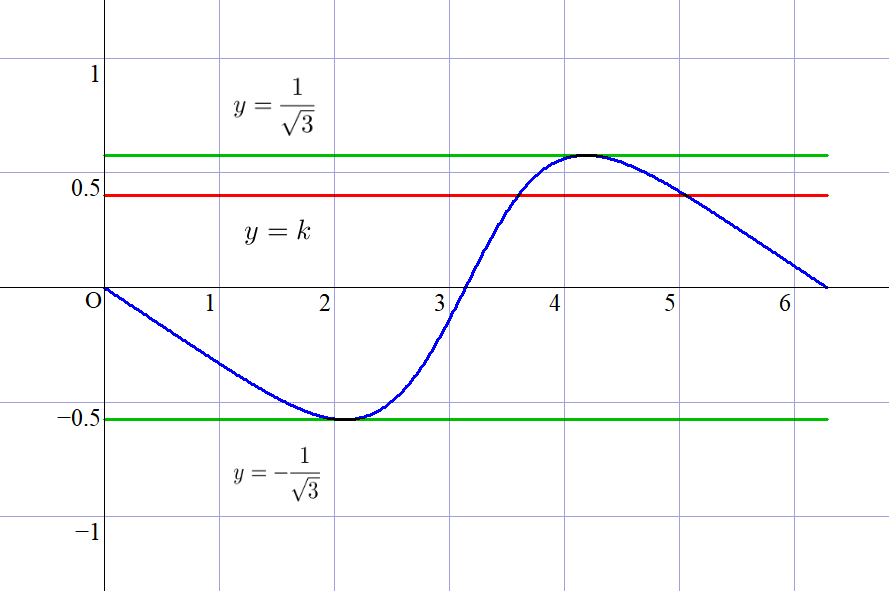
$\quad y=f(\theta)=-\cfrac{\sin \theta}{2+\cos \theta} \quad は \ 2\pi\ を周期とする周期関数であるから区間 \ [0,\ 2\pi]\ のグラフを考えればよい。$
$\quad y'=-\cfrac{\cos \theta(2+\cos \theta)+\sin ^2\theta}{(2+\cos \theta)^2}=-\cfrac{1+2\cos \theta}{(2+\cos \theta)^2}$
\[
\begin{array}{c||c|c|c|c|c}
\hline
\theta & 0 & \cdots & \cfrac{2\pi}{3} & \cdots & \cfrac{4\pi}{3}& \cdots &2\pi\\
\hline
y' & & - & 0 & + & 0 & - & \\
\hline
y & 0 & \searrow & 極小 & \nearrow & 極大 & \searrow & 0 \\
\end{array}
\]
$\quad y=f(\theta)\ は$
$\quad x =\cfrac{2\pi}{3} \ \ で極小かつ最小、最小値は \quad y=-\cfrac{1}{\sqrt{3}}$
$\quad x =\cfrac{4\pi}{3} \ \ で極大かつ最大、最大値は \quad y=\cfrac{1}{\sqrt{3}}$
$\quad グラフは右のとおりで、このグラフと \ y=k \ が交点をもつのは \qquad -\cfrac{1}{\sqrt{3}} \leqq k \leqq \cfrac{1}{\sqrt{3}} \quad のとき$
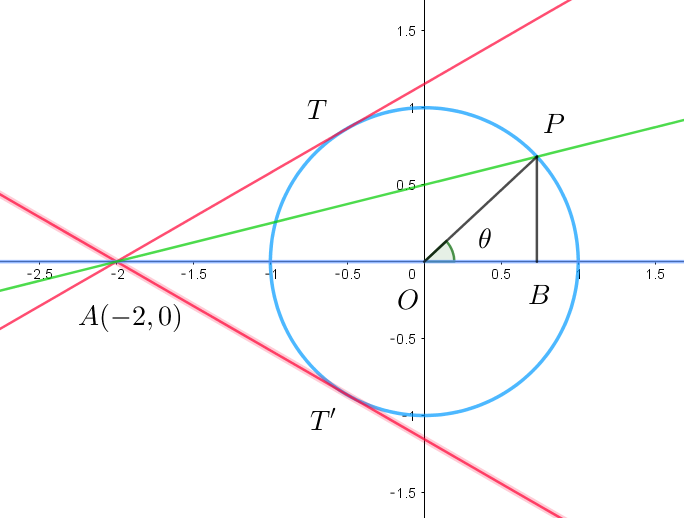
$解法4 \quad (図形的に求める方法)$
$原点Oを中心とし、半径1の円周上に点Pをとり、$
$点Pからx軸に下ろした垂線の足をBとする。$
$\angle POB=\theta \ \ とし、 \quad 点A(-2,0)\ \ をとる。$
$\quad OB=\cos \theta ,\quad PB=\sin \theta ,\quad AB=2+\cos \theta \quad だから$
$\cfrac{\sin \theta}{2+\cos \theta} =\cfrac{PB}{AB} \quad となり、これは直線APの傾きである。$
$点Pが円周上を動いたとき、この直線の傾きの最大と最小は直線APが円の接線のときである。$
$接点をT,T'とすると$
$\quad OA=2,\quad OT=OT'=1 ,\quad AT \perp OT,\quad AT' \perp OT' $
$したがって \quad \angle OAT=\angle OAT'=\cfrac{\pi}{6}$
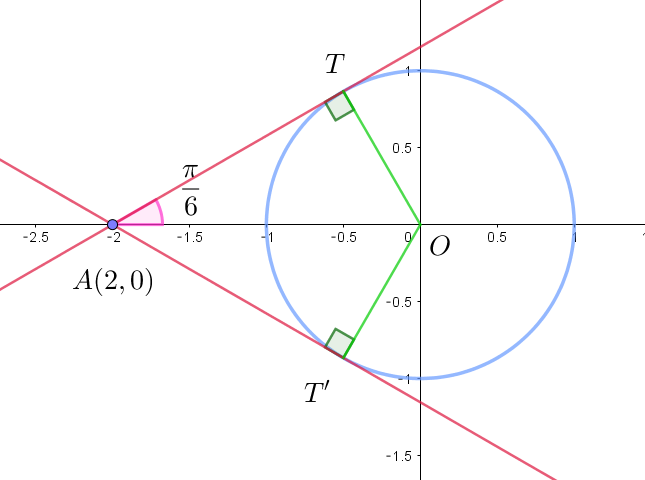
$\quad 直線ATの傾きは \quad \tan \cfrac{\pi}{6}=\cfrac{1}{\sqrt{3}}$
$\quad 直線AT'の傾きは \quad -\tan \cfrac{\pi}{6}=-\cfrac{1}{\sqrt{3}}$
$よって \qquad -\cfrac{1}{\sqrt{3}} \leqq k \leqq \cfrac{1}{\sqrt{3}}$
メインメニュー に戻る