一橋大学 2025年 問題4
$原点を \ O\ とする座標空間内の \ 2\ 点A(0,\ 3,\ -5),\ \ B(5,\ -2,\ 10)\ \ に対して \quad \vec{OP}=s\big\{(1-t)\vec{OA}+t\vec{OB}\big\}$
$ s \geqq 0,\ \ \dfrac{1}{5} \leqq t \leqq \dfrac{3}{5}\ \ で定まる点P\ が存在する範囲を \ D\ とする。D\ に含まれる半径 \ 10\sqrt{2} \ の円のうち、その$
$中心と原点との距離が最小となるものを \ C\ とする。円C\ の中心の座標を求めよ。$
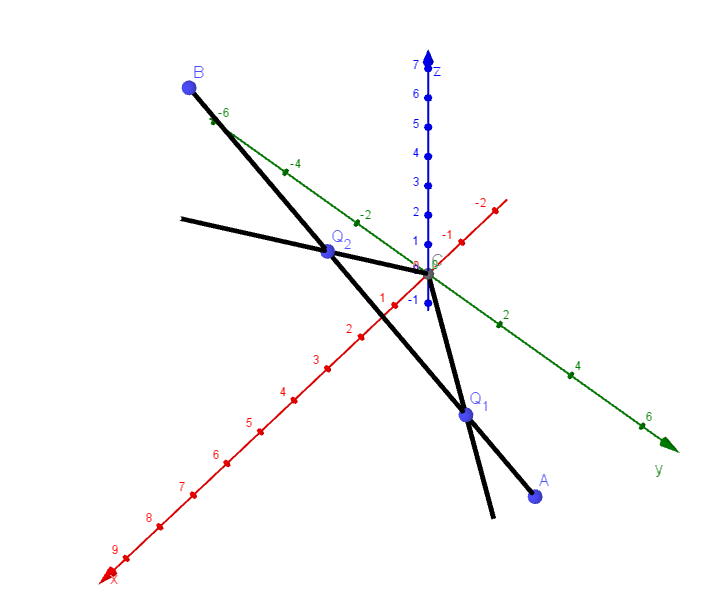
$\vec{OQ_1}=\dfrac{4}{5}(0,\ 3,\ -5)+\dfrac{1}{5}(5,\ -2,\ 10)=(1,\ 2,\ -2)$
$\vec{OQ_2}=\dfrac{2}{5}(0,\ 3,\ -5)+\dfrac{3}{5}(5,\ -2,\ 10)=(3,\ 0,\ 4)$
$\vec{OQ_1} \ と \ \vec{OQ_2}\ のなす角を \ 2\alpha \quad (0 < \alpha < \dfrac{\pi}{2})\quad とおくと$
$\cos 2\alpha =\dfrac{\vec{OQ_1} \cdot \vec{OQ_2}}{|\vec{OQ_1}||\vec{OQ_2}|}=\dfrac{3-8}{\sqrt{9} \times \sqrt{25}}=-\dfrac{1}{3}$
$\sin ^2\alpha=\dfrac{1}{2}(1-\cos 2\alpha)=\dfrac{1}{2}(1+\dfrac{1}{3})=\dfrac{2}{3}$
$\therefore \sin \alpha =\sqrt{\dfrac{2}{3}}$
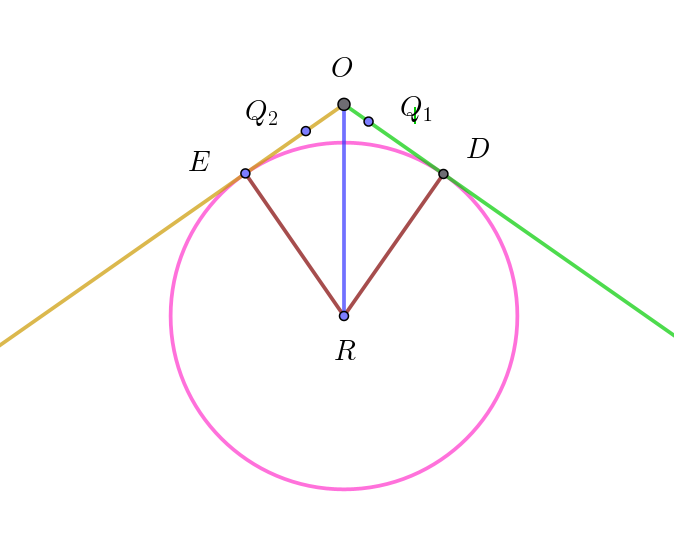
$円C\ の中心と原点との距離が最小となるのは$
$円C\ が直線OQ_1,\ \ OQ_2 \ \ に接する場合だから$
$(ロートを逆さまにして、ビー玉を入れるとどうなるか考えればわかる。)$
$接点をそれぞれ \ \ D,\ \ E ,\ \ 円C\ の中心を \ R\ とすると$
$RD \perp OD,\quad RE \perp OE$
$\triangle ORD \equiv \triangle ORE \quad だから \quad \angle ROD=\angle ROE=\alpha $
$OR=\dfrac{RD}{\sin \alpha}=10\sqrt{2} \times \sqrt{\dfrac{3}{2}}=10\sqrt{3}$
$OD=OE=\sqrt{OR^2-RD^2}=\sqrt{300-200}=10$
$OQ_1=3,\quad OQ_2=5 \quad だから$
$\vec{OD}=\dfrac{10}{3}\vec{OQ_1}=\dfrac{10}{3}(1,\ 2,\ -2),\qquad \vec{OE}=\dfrac{10}{5}\vec{OQ_2}=2(3,\ 0,\ 4)$
$対称性から、\vec{OD}+\vec{OE}\ は \ OR\ 方向のベクトルである。$
\begin{eqnarray*} \vec{OR} &=&k(\vec{OD}+\vec{OE})\\ \\ &=&k\big((\dfrac{10}{3},\dfrac{20}{3},-\dfrac{20}{3})+(6,\ 0,\ 8)\big)\\ \\ &=&k(\dfrac{28}{3},\dfrac{20}{3},\dfrac{4}{3})\\ \\ &=&\dfrac{4}{3}k(7,\ 5,\ 1)\\ \end{eqnarray*}
$|\vec{OR}|=\dfrac{4}{3}k \sqrt{7^2+5^2+1^2}=\dfrac{20\sqrt{3}}{3}k$
$OR=10\sqrt{3} \quad だから \quad \dfrac{20\sqrt{3}}{3}k=10\sqrt{3} \qquad \therefore \ \ k=\dfrac{3}{2}$
$\vec{OR}=\dfrac{4}{3} \times \dfrac{3}{2} (7,\ 5,\ 1)=(14,\ 10,\ 2)$
$よって、中心と原点との距離が最小となる円C\ の中心の座標は\ \ (14,\ 10,\ 2)$
メインメニュー に戻る