一橋大学 2025年　問題3


\[等式\ \ 6\int_0^2|x^2-a|dx=a^2-2a+k \quad が成り立つ実数 \ a\ がちょうど \ 4\ つ存在するような実数 \ k\ の範囲を求めよ。\]



\[I=\int_0^2|x^2-a|dx \ \ とおき、k=6I-a^2+2a \quad として　直線 \ \ y=k\ \ と \ \ y=f(a)=6I-a^2+2a \ \ の\]
$交点の個数を調べる。$

　

(i)$\ \ a \leqq 0 \quad のとき$

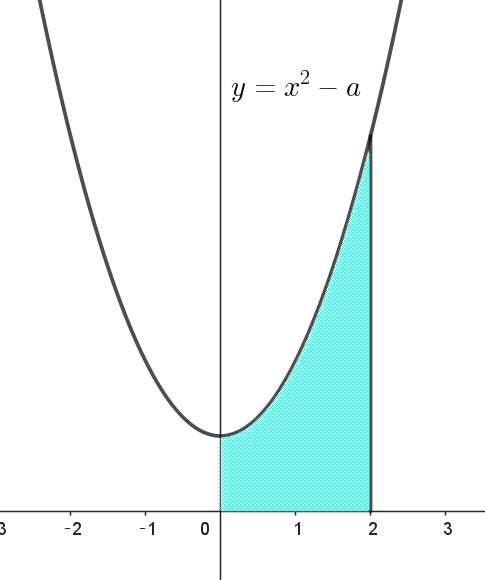
$0 \leqq x \leqq 2 \ \ で \quad |x^2-a|=x^2-a \quad だから$

\[I=\int_0^2 (x^2-a)dx=\big[\dfrac{x^3}{3}-ax\big]_0^2=\dfrac{8}{3}-2a\]
$f(a)=6(\dfrac{8}{3}-2a)-a^2+2a=-a^2-10a+16=-(a+5)^2+41$

　

(ii)$\ \ 0 < a < 4 \quad のとき$

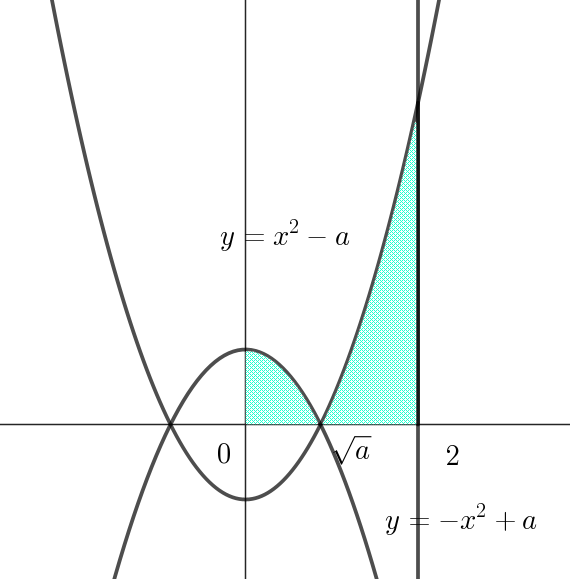
$0 \leqq x \leqq 2 \ \ で$
\[ |x^2-a|= \hspace{1em} \left\{ \begin{array}{l} -x^2+a \hspace{4em}(0 < x \leqq \sqrt{a})\\ x^2-a \hspace{5em}(\sqrt{a} < x \leqq 2)\\ \end{array} \right. \] \begin{eqnarray*} I &=&\int_0^{\sqrt{a}} (-x^2+a)dx+\int_{\sqrt{a}}^2 (x^2-a)dx\\ \\ &=&\big[-\dfrac{x^3}{3}+ax\big]_0^{\sqrt{a}}+\big[\dfrac{x^3}{3}-ax\big]_{\sqrt{a}}^2\\ \\ &=&\big(-\dfrac{a\sqrt{a}}{3} +a\sqrt{a}\big)+\big(\dfrac{8}{3}-2a\big)-\big(\dfrac{a\sqrt{a}}{3}-a\sqrt{a}\big)\\ \\ &=&\dfrac{4}{3}a\sqrt{a}-2a+\dfrac{8}{3} \end{eqnarray*}
$f(a)=6(\dfrac{4}{3}a\sqrt{a}-2a+\dfrac{8}{3})-a^2+2a=-a^2+8a\sqrt{a}-10a+16$

$\sqrt{a}=b\ \ (0 < b < 2) \ \ とおくと \ b\ は \ a\ の単調増加関数だから \ a\ の増減と \ b\ の増減は一致する。$

$g(b)=-b^4+8b^3-10b^2+16 \quad だから$

$g'(b)=-4b^3+24b^2-20b=-4b(b-1)(b-5)$

\[ \begin{array}{c||c|c|c|c|c} b & 0 & \cdots & 1 & \cdots & 2\\ \hline g'(b) & & - & 0 & + \\ \hline g(b) & & \searrow & 極小 & \nearrow & \\ \end{array} \]
$g(b)\ は \ b=1\ のとき極小値 \ \ g(1)=13\ \ をとるから、f(a)\ も \ a=1\ のとき$

$極小値 \ \ f(1)=13\ \ をとる。$

　

(iii)$\ \ a > 4 \quad のとき\ \ $

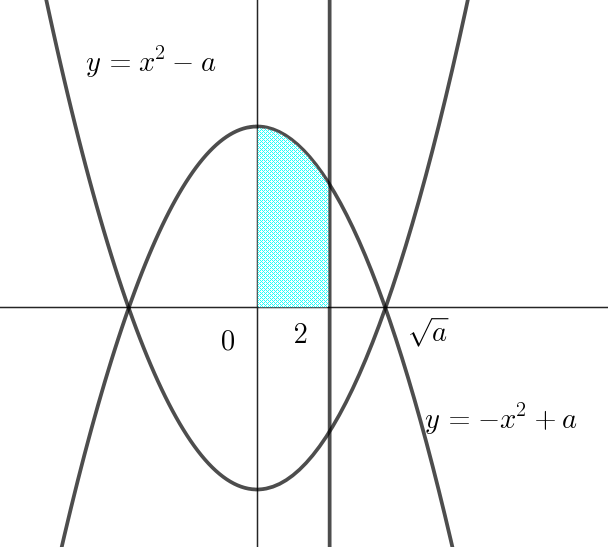
$0 \leqq x \leqq 2 \ \ で \quad |x^2-a|=-x^2+a \quad だから$

\[I=\int_0^2 (-x^2+a)dx=\big[-\dfrac{x^3}{3}+ax\big]_0^2=-\dfrac{8}{3}+2a\]
$f(a)=6(-\dfrac{8}{3}+2a)-a^2+2a=-a^2+14a-16=-(a-7)^2+33$


(i),(ii),(iii)$をまとめた\ \ y=f(a)\ のグラフは右図のとおり$

　

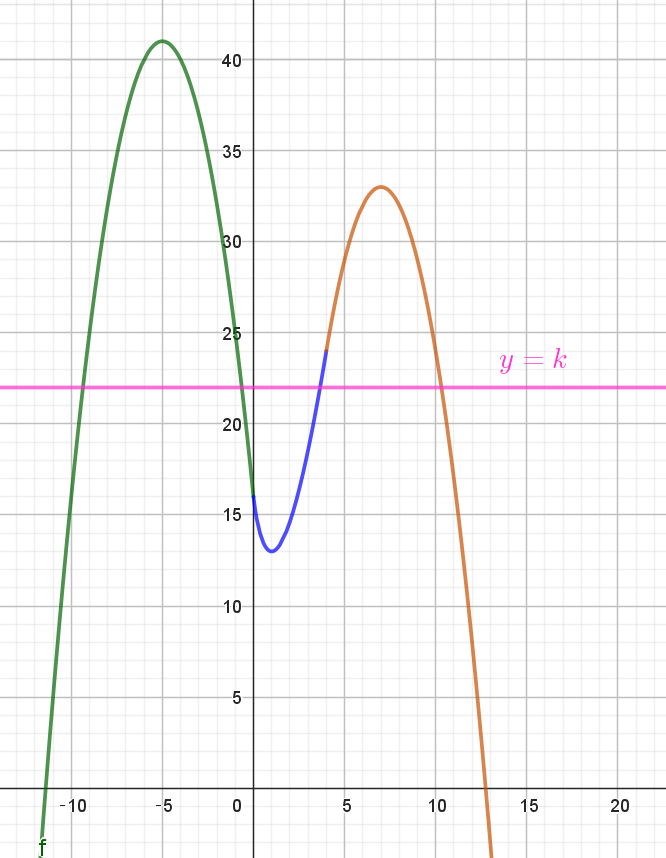
\[よって等式\ \ 6\int_0^2|x^2-a|dx=a^2-2a+k \quad が成り立つ\]
$実数 \ a\ がちょうど \ 4\ つ存在するような実数 \ k\ の範囲は$

$ 13 < k < 33$


ページの先頭へ↑




メインメニュー　に戻る