一橋大学 2025年　問題2


$座標平面上に原点を中心とする半径 \ 3\ の円C_1\ がある。また、直線 \ x=2\ 上の点P\ を中心とする半径 \ 1\ の$
$円をC_2\ とする。$
$(1)\ \ C_1\ と \ C_2\ が共有点を \ 2\ つ持つような \ P\ の \ y\ 座標の範囲を求めよ。$
$(2)\ \ C_1\ と \ C_2\ が共有点を \ 2\ つ持つとき、その \ 2\ つの共有点を通る直線を \ \ell \ とする。\ell \ に関して \ P\ と対称な$
$\quad 位置にある点を \ Q\ とする。ただし、P\ が \ \ell \ 上にあるときは \ Q=P\ とする。P\ の \ y\ 座標が(1)で求めた$
$\quad 範囲を動くとき、点Q\ の軌跡を求め、図示せよ。$


(1)

　

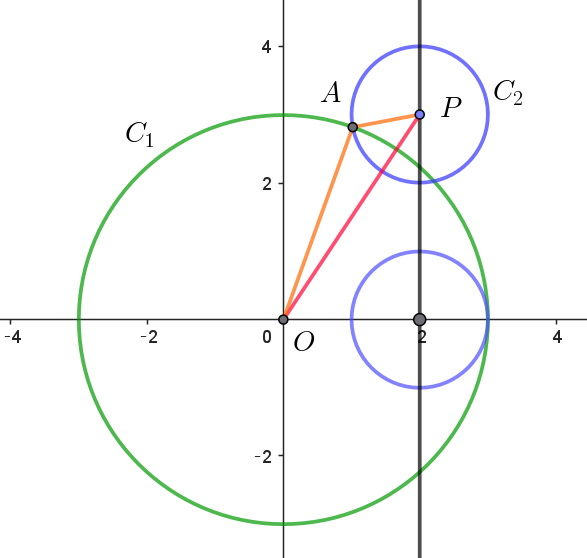
$P(2,\ p)\ \ とおくと、グラフは \ x\ 軸について対称だから \ \ p \geqq 0 とする。$

$C_1\ と \ C_2\ が共有点を \ 2\ つ持つとき、その \ 1\ つを \ A\ とすると$

$\triangle OAP \ \ において \quad OP < OA+AP \quad が成りたつから$

$\sqrt{2^2+p^2}<3+1$

$4+p^2 < 16$

$p<2\sqrt{3}$

$対称性から \quad -2\sqrt{3} < p <2\sqrt{3}$

$ただし、p=0 \ \ のときは右図のとおり、C_1\ と \ C_2\ は内接するから共有点は \ 1\ つである。$

$したがって \quad C_1\ と \ C_2\ が共有点を \ 2\ つ持つような \ P\ の \ y\ 座標の範囲は$

$-2\sqrt{3} < p <2\sqrt{3} \quad ただし \ \ p \ne 0$


(2)

　

$C_1\ と \ C_2\ の \ 2\ つの共有点を通る直線 \ \ell \ は$

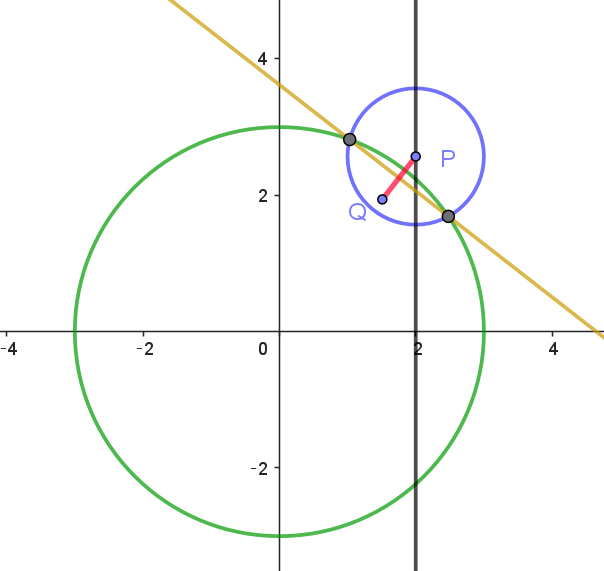
$C_1:x^2+y^2=9 \hspace{10em}①$

$C_2:(x-2)^2+(y-p)^2=1 \hspace{5em}②$

$①-②より$

$\ell : 4x+2py-p^2-12=0$

$Q(t,\ u)\ \ とおくと$

(i)$\ \ P,\ Q\ の中点 \ \ \big(\dfrac{2+t}{2},\ \dfrac{p+u}{2}\big) \ \ は \ \ell \ 上にあるから$

$\quad 4 \times \dfrac{2+t}{2}+2p \times \dfrac{p+u}{2}-p^2-12=0$

$\quad 2t+pu=8 \hspace{10em}③$

(ii)$\ \ PQ \perp \ell \quad だから$

$\quad \dfrac{u-p}{t-2} \times \big(-\dfrac{2}{p}\big)=-1$

$\quad 2(u-p)=p(t-2)$

$\quad 2u=pt \hspace{12em}④$

$p=\dfrac{2u}{t} \ \ を③に代入して$

$2t+\dfrac{2u^2}{t}=8$

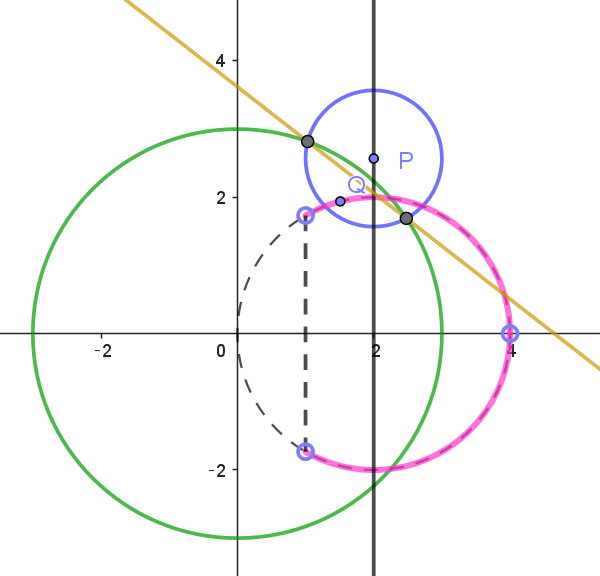
$t^2+u^2=4t$

$(t-2)^2+u^2=4$

　

$これが点Q\ の軌跡である。ただし \quad ④を③に代入して$

$2t+\dfrac{p^2}{2}t=8$

$p^2=\dfrac{16-4t}{t}$

$(1)より \quad 0 < p^2 < 12 \quad だから \quad 0 < \dfrac{16-4t}{t} < 12$

$t > 0 \quad だから \quad 0 < 16-4t<12t$

$\therefore \ \ 1 < t < 4$

$図は右図のピンク色の円の一部で、t=1,\ \ 4\ \ を除く$


ページの先頭へ↑




メインメニュー　に戻る