MY MATH NOTE

一橋大学 2018年　問題4

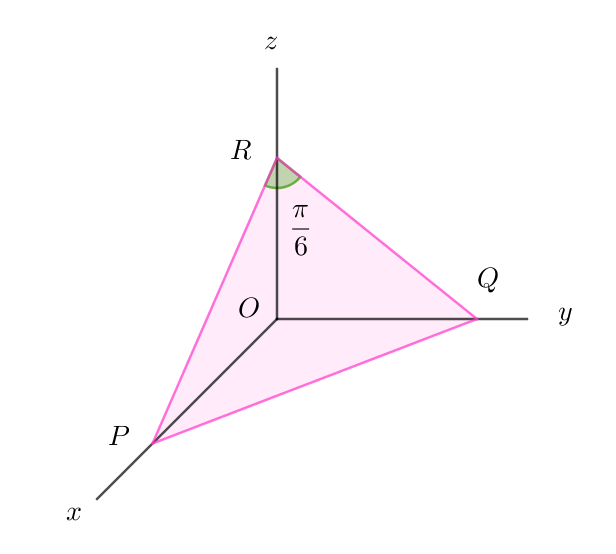
$p,\ q\ を正の実数とする。原点を \ O\ とする座標空間内の \ 3\ 点 \ P(p,\ 0,\ 0),\ Q(0,\ q,\ 0),\ R(0,\ 0,\ 1)\ は$
$\angle PRQ=\cfrac{\pi}{6}\ を満たす。四面体 \ OPQR\ の体積の最大値を求めよ。$

　
$四面体 \ OPQR\ の体積を \ V\ とすると$

$\quad V=\cfrac{1}{3} \times \triangle OPQ \times OR=\cfrac{1}{3} \times \cfrac{1}{2}pq \times 1=\cfrac{pq}{6} \hspace{5em}(1)$

$\triangle PQR\ に余弦定理を用いて$

$\quad PQ^2=PR^2+QR^2-2PR \cdot QR \cdot \cos \cfrac{\pi}{6}$

$\quad p^2+q^2=(p^2+1)+(q^2+1)-2\sqrt{p^2+1}\sqrt{q^2+1} \times \cfrac{\sqrt{3}}{2}$

$\quad 2-\sqrt{3}\sqrt{p^2+1}\sqrt{q^2+1}=0$

$\quad (p^2+1)(q^2+1)=\cfrac{4}{3}$

$\quad p^2q^2+p^2+q^2=\cfrac{1}{3} \hspace{10em}(2)$

$\quad p^2q^2+(p+q)^2-2pq=\cfrac{1}{3}$

$(1)より \quad pq=6V \quad を代入して$

$\quad (p+q)^2=-36V^2+12V+\cfrac{1}{3}$

$相加・相乗平均の不等式より$

$\quad (p+q)^2 \geqq 4pq \quad だから$

$\quad -36V^2+12V+\cfrac{1}{3} \geqq 4pq$

$\quad -36V^2+12V+\cfrac{1}{3} \geqq 24V$

$\quad 108V^2+36V-1 \leqq 0$

$\quad V \leqq \cfrac{-18+\sqrt{18^2+108}}{108}=\cfrac{-18+12\sqrt{3}}{108}=\cfrac{-3+2\sqrt{3}}{18}$

$よって　V\ の最大値は \quad \cfrac{-3+2\sqrt{3}}{18}$

$等号が成りたつのは \ \ p=q \quad のときだから(2)に代入して$

$\quad p^4+2p^2=\cfrac{1}{3} \quad より$

$\quad 3p^4+6p^2-1=0$

$\quad p^2=\cfrac{-3+\sqrt{9+3}}{3}=\cfrac{2\sqrt{3}-3}{3}$

$\quad \therefore \ \ p=q=\sqrt{\cfrac{2\sqrt{3}-3}{3}}\quad のとき$

ページの先頭へ↑