一橋大学 2018年 問題2
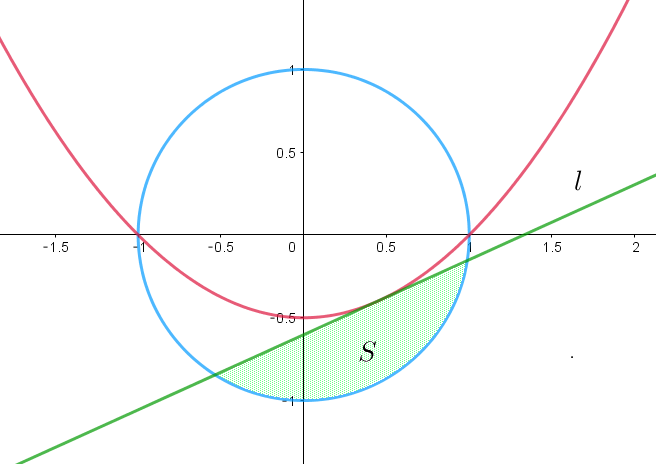
$-1 \leqq t \leqq 1 \ \ とし、曲線 \ \ y=\cfrac{x^2-1}{2}\ \ 上の点 \ (t,\ \cfrac{t^2-1}{2})\ における接線を \ l\ とする。半円 \ \ x^2+y^2=1 \ \ (y \leqq 0)$
$と \ l\ で囲まれた部分の面積を \ S\ とする。S\ のとりうる値の範囲を求めよ。$
$(解説)$
$S\ が最大となるのは \ t=0\ のときで、最小となるのは \ t=\pm 1 \ のときであることは図をかけばわかる。$
$しかし、これをきちんと説明するのは意外に難しい。$
$S\ が円の弓形の面積であることから、円の中心からの距離で \ S\ が決まることから説明がつきます。$
$放物線も円も \ y\ 軸について対象だから \ \ 0 \leqq t \leqq 1 \ \ で考えればよい。$
$点 \ (t,\ \cfrac{t^2-1}{2})\ における接線 \ l\ は$
$\quad y'=x \ \ より \quad y=t(x-t)+ \cfrac{t^2-1}{2} \qquad \therefore tx-y-\cfrac{t^2+1}{2}=0$
$直線と円で囲まれる部分の面積Sは、円の中心と直線との距離 \ h\ によって確定する。$
$すなわち、S\ は \ h\ の関数でもある。$
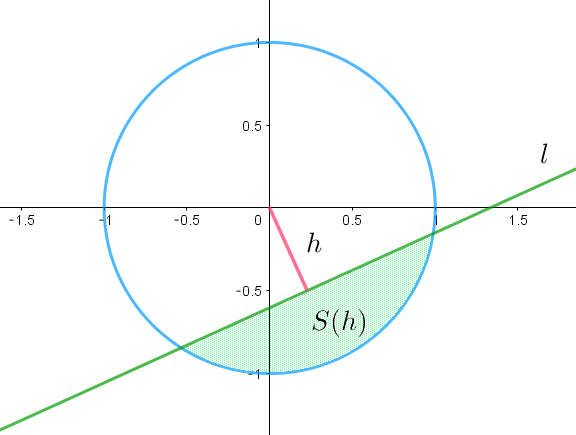
$原点 \ O\ と直線 \ l\ との距離は \quad h=\cfrac{\dfrac{t^2+1}{2}}{\sqrt{t^2+1}}=\cfrac{\sqrt{t^2+1}}{2}$
$\quad h'=\cfrac{t}{2\sqrt{t^2+1}} > 0 \quad だから \quad h\ は区間 \ [0,\ 1]\ で単調増加である。$
$\qquad (文系の受験生は、無理関数の微分法は習っていないと思いますので、$
$\qquad ここはカットしてもよいと思います。)$
$面積 \ S\ は \ h\ が増加すれば逆に減少するから、S\ は \ t\ の関数として区間 \ [0.\ 1]\ で単調減少となる。$
$(1)\ \ Sの最大$
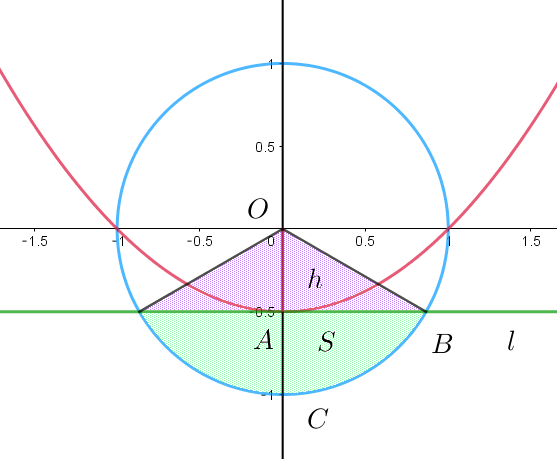
$\quad t=0\ \ のとき \ h\ は最小であるから、S\ は最大となり、最大値は$
$\qquad S=2\big(\pi \times 1^2 \times \cfrac{1}{6}-\cfrac{1}{2} \times \cfrac{1}{2} \times 1 \times \sin 60°\big)=\cfrac{\pi}{3}-\cfrac{\sqrt{3}}{4}$
$(2)\ \ Sの最小$
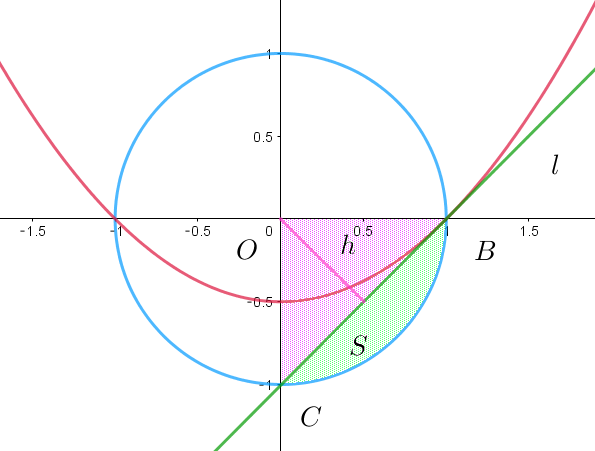
$\quad t=1\ \ のとき \ h\ は最大であるから、S\ は最小となり、最小値は$
$\qquad S=\pi \times 1^2 \times \cfrac{1}{4}-\cfrac{1}{2} \times 1 \times 1 =\cfrac{\pi}{4}-\cfrac{1}{2}$
$したがって、S\ のとりうる値の範囲は$
$\qquad \cfrac{\pi}{4}-\cfrac{1}{2} \leqq S \leqq \cfrac{\pi}{3}-\cfrac{\sqrt{3}}{4}$
メインメニュー に戻る