広島大学(理系) 2025年　問題3


$0 < \theta < \dfrac{\pi}{3} \ を満たす \ \theta \ に対し、座標平面上の原点 \ O(0,\ 0)\ を中心とする半径 \ 1\ の円上の \ 4\ 点 \ A(1,\ 0),$
$B(\cos \theta,\ \sin \theta),\ \ C(\cos 2\theta,\ \sin 2\theta),\ \ D(\cos 3\theta,\ \sin 3\theta)\ を考え、\triangle OAD \ の面積を \ S(\theta),\ \ \triangle ABC の面積をT(\theta),$
$\triangle ABD \ の面積を \ U(\theta)\ \ とする。次の問いに答えよ。$
\[(1)\ \ \lim_{\theta \rightarrow +0} \dfrac{S(\theta)}{\theta} \ \ を求めよ。\] \[(2)\ \ \lim_{\theta \rightarrow +0} \dfrac{T(\theta)}{\theta ^3} \ \ を求めよ。\] $(3)\ \ t=\cos \theta \ \ とおく。\dfrac{U(\theta)}{\sin \theta} \ \ を \ t\ の整式で表せ。$
\[(4)\ \ 関数 \ f(\theta) \ を \ f(\theta)=\dfrac{T(\theta)}{U(\theta)}\ \ と定義する。\lim_{\theta \rightarrow +0} f(\theta) を求めよ。また、\theta \ が \ \ 0 < \theta < \dfrac{\pi}{3}\ \ の範囲を動くとき、\] $\quad f(\theta) \ \ のとり得る値の範囲を求めよ。$


(1)

　

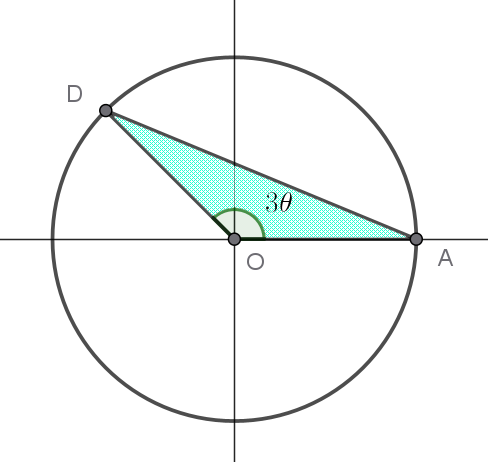
$S(\theta)=\triangle OAD=\cfrac{1}{2} \times OA \times OD \times \sin 3\theta=\cfrac{1}{2}\sin 3\theta$

$\cfrac{S(\theta)}{\theta}=\cfrac{\sin 3\theta}{2\theta}=\cfrac{3}{2} \times \cfrac{\sin 3\theta}{3\theta}$

$\theta \rightarrow +0 \ \ のとき \ \ \cfrac{\sin 3\theta}{3\theta} \longrightarrow 1 \ \ だから$

\[\lim_{\theta \rightarrow +0} \dfrac{S(\theta)}{\theta}=\cfrac{3}{2}\]

(2)

　

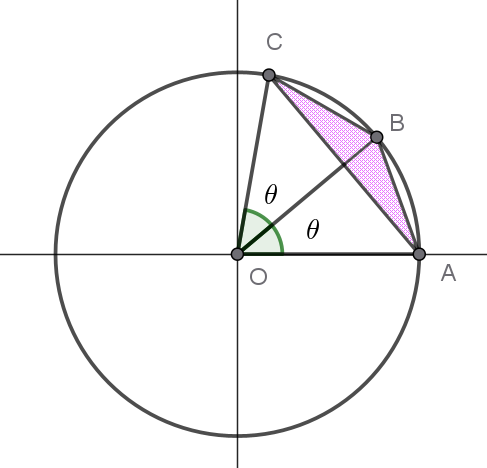
\begin{eqnarray*} T(\theta) &=&\triangle ABC\\ \\ &=&\triangle AOB + \triangle BOC - \triangle AOC\\ \\ &=&\dfrac{1}{2}\sin \theta +\dfrac{1}{2}\sin \theta - \dfrac{1}{2}\sin 2\theta \\ \\ &=&\sin \theta - \sin \theta \cos \theta\\ \\ &=&\sin \theta (1- \cos \theta)\\ \\ &=&2\sin \dfrac{\theta}{2}\cos \dfrac{\theta}{2} \times 2\sin ^2 \dfrac{\theta}{2}\\ \\ &=&4\sin ^3 \dfrac{\theta}{2}\cos \dfrac{\theta}{2}\\ \end{eqnarray*}
$\cfrac{T(\theta)}{\theta ^3}=\cfrac{4\sin ^3 \dfrac{\theta}{2}\cos \dfrac{\theta}{2}}{\theta ^3}= \cfrac{1}{2}\Big(\cfrac{\sin \dfrac{\theta}{2}}{\dfrac{\theta}{2}}\Big)^3 \cos \dfrac{\theta}{2}$

$\theta \rightarrow +0 \ \ のとき \ \ \cfrac{\sin \dfrac{\theta}{2}}{\dfrac{\theta}{2}} \longrightarrow 1 , \cos \dfrac{\theta}{2} \longrightarrow 1 \ \ だから$

\[\lim_{\theta \rightarrow +0} \dfrac{T(\theta)}{\theta ^3}=\cfrac{1}{2}\]

(3)

　

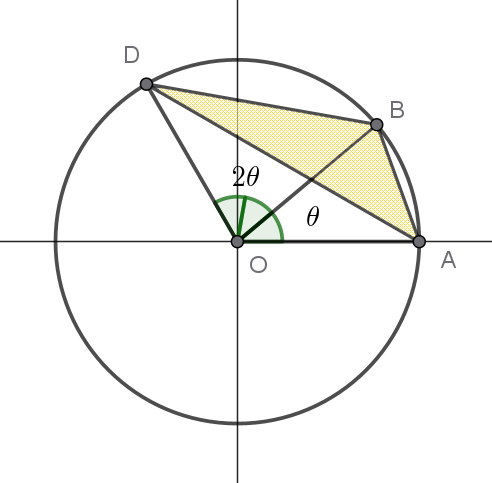
\begin{eqnarray*} U(\theta) &=&\triangle ABD\\ \\ &=&\triangle AOB + \triangle BOD - \triangle AOD\\ \\ &=&\dfrac{1}{2}\sin \theta +\dfrac{1}{2}\sin 2\theta - \dfrac{1}{2}\sin 3\theta \\ \\ &=&\dfrac{1}{2}(\sin \theta - \sin 3\theta )+ \dfrac{1}{2}\sin 2\theta \\ \\ &=&-\cos 2\theta \sin \theta + \sin \theta \cos \theta\\ \\ &=&\sin \theta (\cos \theta - \cos 2\theta)\\ \\ &=&\sin \theta (\cos \theta -(2\cos ^2 \theta -1)\\ \\ &=&\sin \theta (-2\cos ^2 \theta + \cos \theta +1)\\ \end{eqnarray*}
$\therefore \ \ \cfrac{U(\theta)}{\sin \theta }=-2\cos ^2 \theta + \cos \theta +1=-2t^2+t+1$


(4)


$(2)より \quad T(\theta)=\sin \theta (1- \cos \theta) \ \ だから$

\begin{eqnarray*} f(\theta) &=&\dfrac{T(\theta)}{U(\theta)}\\ \\ &=&\dfrac{\sin \theta (1- \cos \theta)}{\sin \theta (-2\cos ^2 \theta + \cos \theta +1)}\\ \\ &=&\dfrac{1- \cos \theta}{(1-\cos \theta)(1 + 2\cos \theta )}\\ \\ &=&\dfrac{1}{1+2\cos \theta}\\ \end{eqnarray*} \[\therefore \ \ \lim_{\theta \rightarrow +0} f(\theta) =\lim_{\theta \rightarrow +0} \dfrac{1}{1+2\cos \theta }=\cfrac{1}{3}\]

　

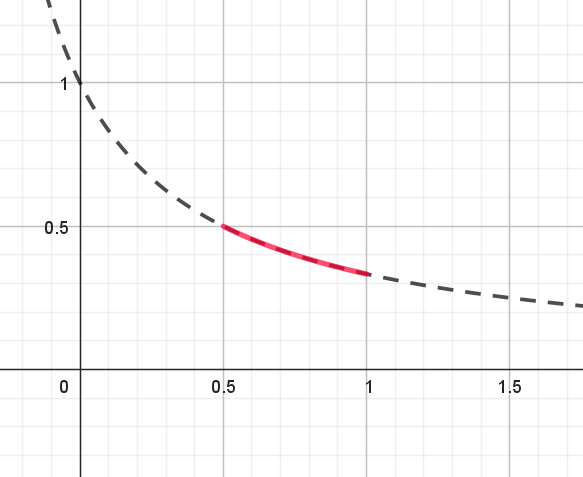
$t=\cos \theta \ \ とおくと \ \ 0 < \theta < \dfrac{\pi}{3}\ \ のとき \quad \dfrac{1}{2} < t < 1$

$g(t)=\dfrac{1}{1+2t} \ \ のグラフは右図のとおり$

$g(\dfrac{1}{2})=\dfrac{1}{2},\quad g(1)=\dfrac{1}{3} \ \ だから \quad \dfrac{1}{3} < g(t) < \dfrac{1}{2} $

$よって \quad \dfrac{1}{3} < f(\theta) < \dfrac{1}{2} $


ページの先頭へ↑




メインメニュー　に戻る