広島大学(理系) 2025年　問題2


$a > 0 \ とし、p\ を実数とする。座標平面上の \ 3\ 点A(0,\ a),\ B(-1,\ 0),\ C(1,\ 0)\ を考える。点P_n,\ Q_n,\ R_n$
$(n=1,\ 2,\ 3,\ \cdots)\ が以下の二つの条件を満たすとする。$
(i)$\ \ 点P_1\ は直線AB\ 上にあり、x\ 座標が \ p\ である。$
(ii)$\ \ 自然数 \ n\ に対し、$
$\qquad ・点P_n \ から \ x\ 軸に下した垂線と \ x\ 軸との交点が \ Q_n \ である。ただし、点P_n \ が \ x\ 軸にあるときは、$
$\hspace{3em} 点Q_n \ は \ P_n \ と同じ点であるとする。$
$\qquad ・点Q_n \ から直線AC\ に下した垂線と直線AC\ との交点がR_n \ である。ただし、点Q_n \ が直線AC\ 上に$
$\hspace{3em} あるときは、点R_n \ は \ Q_n \ と同じ点であるとする。$
$\qquad ・点R_n \ を通り、x\ 軸と平行な直線と直線AB\ との交点が \ P_{n+1}\ である。$
$点P_n \ の \ x\ 座標を \ x_n \ とする。次の問いに答えよ。$
$(1)\ \ 点R_1\ の座標を \ a,\ p\ を用いて表せ。$
$(2)\ \ 命題「点P_1\ が線分AB\ 上にあるならば、点R_1\ は線分AC\ 上にある」が真であるような \ a\ の値の範囲を$
$\quad 求めよ。ただし、線分は両端を含むものとする。$
$(3)\ \ x_n \ を \ a,\ n,\ p\ を用いて表せ。$
$(4)\ \ a=2,\ p=0\ であるとき、不等式 \ \ |x_{n+1} - x_n | < 10^{-10} \ \ を満たす最小の自然数 \ n\ を求めよ。ただし、$
$\quad \log _{10}2=0.3010 \ \ とする。$


(1)

　

$点P_1\ は直線AB\ 上にあり、x\ 座標が \ p\ だから \ \ Q_1(p,\ 0)$

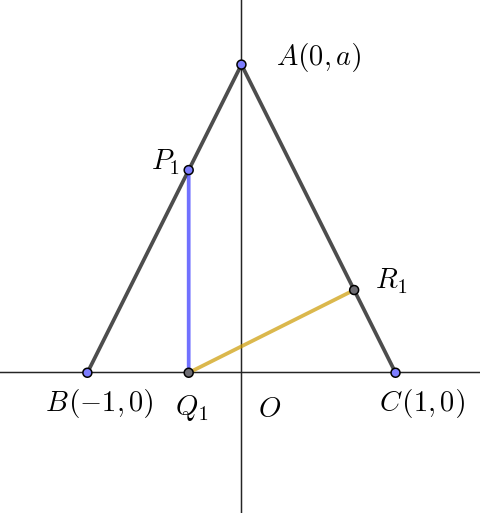
$直線 \ AC\ の傾きは \ -a\ だから、Q_1R_1\ の傾きは \ \ \cfrac{1}{a}$

$よって、直線 \ Q_1R_1\ の方程式は \ \ y=\cfrac{1}{a}(x-p)$

$直線 \ Q_1R_1\ と \ AC\ の交点が \ R_1\ \ だから$

$\cfrac{1}{a}(x-p)=-ax+a$

$(a+\cfrac{1}{a})x=a+\cfrac{p}{a}$

$(a^2+1)x=a^2+p \qquad \therefore \ \ x=\cfrac{a^2+p}{a^2+1}$

$y=-a \times \cfrac{a^2+p}{a^2+1}+a=\cfrac{a(1-p)}{a^2+1}$

$よって \quad R_1\big(\cfrac{a^2+p}{a^2+1},\ \cfrac{a(1-p)}{a^2+1}\big)$


(2)

　

$(研究)$

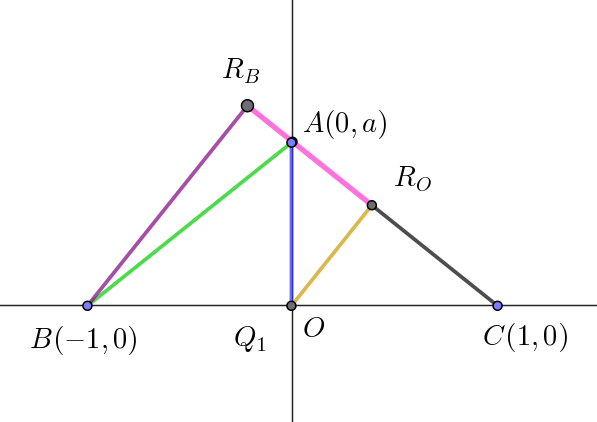
$点A(0,\ a) の位置によっては、右図のように、P_1 \ が \ A\ に一致する$

$ときは、Q_1=O\ だから \ O\ から直線 \ AC\ に下した垂線との交点 \ R_O \ は$

$線分 \ AC\ 上にある。P_1\ が \ B\ に一致するときは、Q_1=B \ だから \ B\ から$

$直線 \ AC\ に下した垂線との交点R_B は線分CAの延長上にある。$

$そこで、点P_1\ が線分AB\ 上にあるならば、点R_1\ が必ず線分AC\ 上にある$

$ような \ a\ の値の範囲を求めるのがこの問題である。$


$点P_1\ が線分AB\ 上にある条件は、-1 \leqq p \leqq 0$

$点P_1 \longrightarrow R_1 \ \ への対応を考え、とくにそれらの \ x\ 座標を対応させる写像を\ \varphi \ とする。$

$U=[-1,\ 0]\ の任意の実数 \ p\ に対して、(1)より\ \ \varphi(p)=\cfrac{a^2+p}{a^2+1}$

$両辺に \ a^2\ を加えて \quad a^2-1 \leqq a^2+p \leqq a^2$

$両辺を\ a^2+1 \ で割って \quad \cfrac{a^2-1}{a^2+1} \leqq \cfrac{a^2+p}{a^2+1} \leqq \cfrac{a^2}{a^2+1}$

$\therefore \ \ \cfrac{a^2-1}{a^2+1} \leqq \varphi(p) \leqq \cfrac{a^2}{a^2+1}$

$すなわち \quad \varphi(U)=\big\{\dfrac{a^2-1}{a^2+1} , \dfrac{a^2}{a^2+1}\big\} $

　

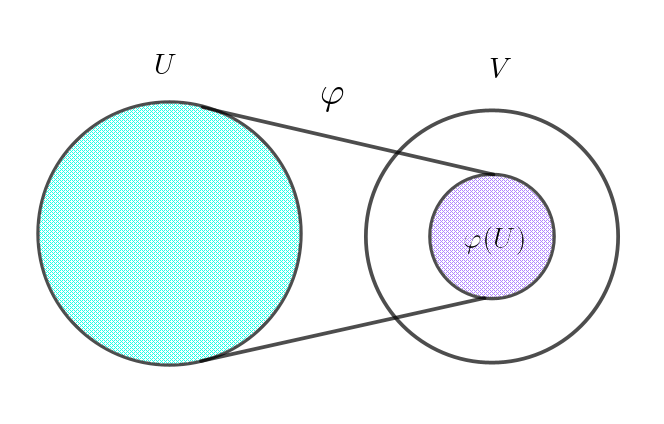
$点R_1\ が線分AC\ 上にある条件は \ \ 0 \leqq \varphi(p) \leqq 1 \ \ を満たすことであるから$

$V=[0,\ 1]\ とおくと$

$「点P_1\ が線分AB\ 上にあるならば、点R_1\ は線分AC\ 上にある」が真$

$であるとは \quad \varphi(U) \subset V \ \ が成りたつことである。$

$\dfrac{a^2}{a^2+1} < 1 \ \ だから \ \ 0 \leqq \dfrac{a^2-1}{a^2+1}\ \ であればよい。$

$0 \leqq a^2-1 \ \ より \quad a > 0 \ \ だから \quad a \geqq 1$


(3)

　

$P_n(x_n,\ y_n)\ とおくと(1) で求めた \ R_1 \ の \ x\ 座標で、p=x_n \ \ とおいて$

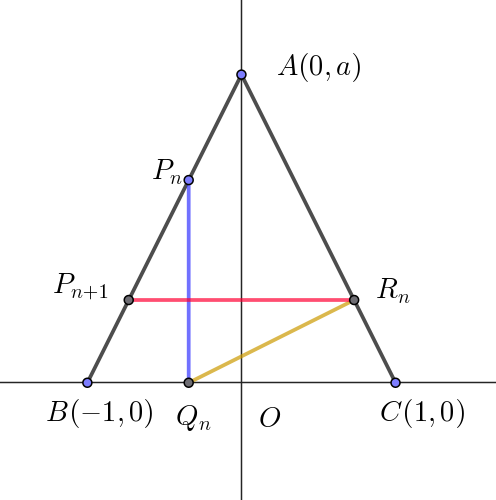
$R_n \ の \ x\ 座標は \ \ \cfrac{a^2+x_n}{a^2+1}$

$直線 \ AC\ と \ AB\ は \ y\ 軸に関して対称だから$

$点P_{n+1} \ と点 \ R_n \ は \ y\ 軸に関して対称である。$

$したがって \quad x_{n+1}=-\dfrac{a^2+x_n}{a^2+1}$

$x_{n+1}=-\dfrac{1}{a^2+1}x_n -\dfrac{a^2}{a^2+1}$

$t=-\dfrac{1}{a^2+1}t -\dfrac{a^2}{a^2+1} \ \ を解いて \ \ t=-\dfrac{a^2}{a^2+2}$

$辺々引いて$

$x_{n+1}+\dfrac{a^2}{a^2+2}=-\dfrac{1}{a^2+1}(x_n+ \dfrac{a^2}{a^2+2})$

$x_n+\dfrac{a^2}{a^2+2}=(x_1+ \dfrac{a^2}{a^2+2})(-\dfrac{1}{a^2+1})^{n-1}$

$x_1=p \ \ だから$
　
$x_n=(p+ \dfrac{a^2}{a^2+2})(-\dfrac{1}{a^2+1})^{n-1}-\dfrac{a^2}{a^2+2}$


(4)


$a=2,\ p=0\ \ のとき$

$x_n=\dfrac{4}{6}(-\dfrac{1}{5})^{n-1}-\dfrac{4}{6}=\dfrac{2}{3}(-\dfrac{1}{5})^{n-1}-\dfrac{2}{3}$

\begin{eqnarray*} & &x_{n+1}-x_n\\ \\ &=&\big\{\dfrac{2}{3}(-\dfrac{1}{5})^n-\dfrac{2}{3}\big\}-\big\{\dfrac{2}{3}(-\dfrac{1}{5})^{n-1}-\dfrac{2}{3}\big\}\\ \\ &=&\dfrac{2}{3}\{(-\dfrac{1}{5})^n- (-\dfrac{1}{5})^{n-1}\}\\ \\ &=&\dfrac{2}{3} \times \big\{(-\dfrac{1}{5})-1\big\} (-\dfrac{1}{5})^{n-1}\\ \\ &=&-\dfrac{4}{5} (-\dfrac{1}{5})^{n-1}\\ \\ &=&4(-\dfrac{1}{5})^n\\ \end{eqnarray*}
$|x_{n+1} - x_n | < 10^{-10} \ \ より$

$\cfrac{4}{5^n} < 10^{-10}$

$5^n > 4 \times 10^{10}$

$n\log 5 > 10+\log 4$

\begin{eqnarray*} n &>&\cfrac{10+\log 4}{\log 5}\\ \\ &=&\cfrac{10+2\log 2}{\log 10-\log 2}\\ \\ &=&\cfrac{10+2 \times 0.3010}{1-0.3010}\\ \\ &>&15.1 \end{eqnarray*}
$これを満たす最小の自然数 \ n\ は \quad n=16$


ページの先頭へ↑




メインメニュー　に戻る