広島大学(理系) 2025年 問題1
$次の問いに答えよ。ただし、\log \ は自然対数を表す。$
$(1)\ \ x > 0\ で定義された次の関数の最大値を求めよ。 \quad f(x)=\dfrac{\log x}{\sqrt{x}}$
$(2)\ \ 次の不定積分をそれぞれ求めよ。$
\[ \qquad \int \log x dx,\qquad \int (\log x)^2 dx\]
$(3)\ \ (1)で求めた最大値を \ a\ として、座標平面上の二つの曲線 \ C_1:y=a\sqrt{x},\ \ C_2: y=\log x \ \ を考える。$
$\quad x\ 軸と二つの曲線 \ C_1,\ C_2\ によって囲まれた図形を \ x\ 軸のまわりに \ 1\ 回転してできる立体の体積 \ V$
$\quad を求めよ。$
(1)
$f(x)=\dfrac{\log x}{\sqrt{x}} \quad より$
\begin{eqnarray*} f'(x) &=&\cfrac{\dfrac{1}{x} \times \sqrt{x} -\log x \times \dfrac{1}{2\sqrt{x}}}{x}\\ \\ &=&\cfrac{\dfrac{1}{\sqrt{x}} - \dfrac{\log x}{2\sqrt{x}}}{x}\\ \\ &=&\cfrac{2-\log x}{2x\sqrt{x}} \\ \end{eqnarray*}
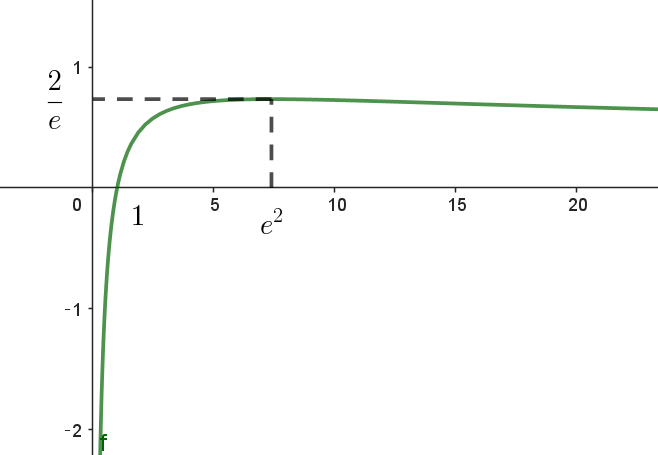
\[ \begin{array}{c||c|c|c|c|c} x& 0 & \cdots & e^2 & \cdots \\ \hline f'(x)& & + & 0 & - \\ \hline f(x)& & \nearrow & 極大 & \searrow & \\ \end{array} \] $f(x)\ は \ \ x=e^2\ \ で極大かつ最大となり、最大値は$
$f(e^2)=\cfrac{\log e^2}{\sqrt{e^2}}=\cfrac{2}{e}$
(2)
\begin{eqnarray*} \int \log x dx &=&x\log x -\int x \cdot \dfrac{1}{x}dx\\ \\ &=&x\log x -x +C \quad (C\ は積分定数) \end{eqnarray*}
\begin{eqnarray*} \int (\log x)^2 dx &=&x(\log x)^2 -\int x \cdot 2\log x \cdot \dfrac{1}{x}dx\\ \\ &=&x(\log x)^2 - 2\int \log x dx\\ \\ &=&x(\log x)^2 - 2(x\log x -x)+C\\ \\ &=&x(\log x)^2 - 2x\log x +2x +C \quad (C\ は積分定数) \end{eqnarray*}
(3)
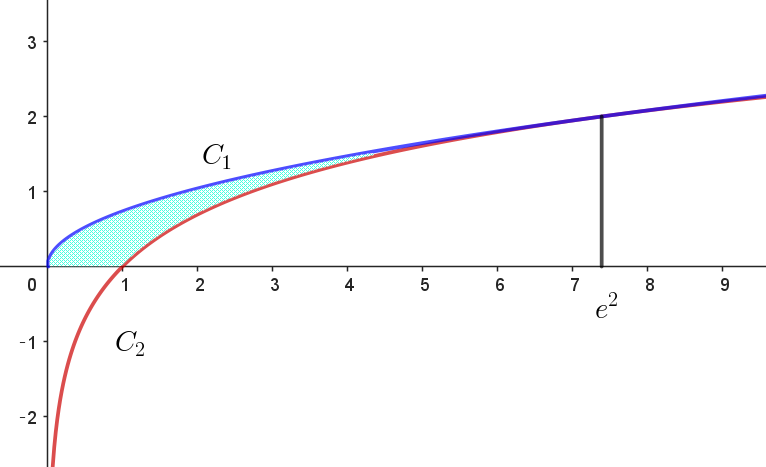
$C_1\ と \ C_2\ の共有点は \quad \cfrac{2}{e}\sqrt{x}=\log x$
$\cfrac{\log x}{\sqrt{x}}=\cfrac{2}{e}$
$(1) より \ \ f(x)=\cfrac{\log x}{\sqrt{x}}\ \ は \ \ x=~e^2 \ \ で最大値 \ \ y=\cfrac{2}{e}\ \ をもつから$
$これを満たす \ x\ はただ一つあり、x=e^2 \ \ である。$
$したがって求める回転体の体積 \ V\ は$
\begin{eqnarray*} V &=&\pi \int_0^{e^2} \big(\dfrac{2}{e}\sqrt{x}\big)^2dx - \pi\int_1^{e^2}(\log x)^2dx\\ \\ &=&\pi \int_0^{e^2} \dfrac{4}{e^2}xdx - \pi\int_1^{e^2}(\log x)^2dx \hspace{5em}(定積分は(2)より)\\ \\ &=&\cfrac{2\pi}{e^2}\big[x^2\big]_0^{e^2}-\pi\big[x(\log x)^2-2x\log x +2x\big]_1^{e^2}\\ \\ &=&\cfrac{2\pi}{e^2} \times e^4 -\pi\{e^2(\log e^2)^2-2e^2\log e^2 + 2e^2-2\}\\ \\ &=&2\pi e^2-\pi(4e^2-4e^2+2e^2-2)\\ \\ &=&2\pi \end{eqnarray*}
メインメニュー に戻る