広島大学(理系) 2018年 問題2
$複素数平面上の4点A(\alpha),B(\beta),C(\gamma),D(\delta)を頂点とする四角形ABCDを考える。$
$ただし、四角形ABCDは、すべての内角が180°より小さい四角形(凸四角形)であるとする。$
$また、四角形ABCDの頂点は反時計回りにA,B,C,Dの順に並んでいるとする。四角形ABCDの$
$外側に、4辺AB,BC,CA,DAをそれぞれ斜辺とする直角二等辺三角形APB,BQC,CRD,DSAを作る。$
$次の問いに答えよ。$
$(1)\ \ 点Pを表す複素数を求めよ。$
$(2)\ \ 四角形PQRSが平行四辺形であるための必要十分条件は、四角形ABCDがどのような$
$\qquad 四角形であるか答えよ。$
$(3)\ \ 四角形PQRSが平行四辺形であるならば、四角形PQRSは正方形であることを示せ。$
$(解説)$
$(1)\ \ 直角二等辺三角形という内容を複素数で表現します。$
$(2)\ \ (1)をつかって、四角形ABCDの向かい合う2辺のベクトルが等しいことを導きます。$
$(3)\ \ (1)と(2)をつかって、四角形PQRSが正方形であることを示せばよいのですが、複素数では何がいえれば$
$\qquad よいか考えます。$
(1)
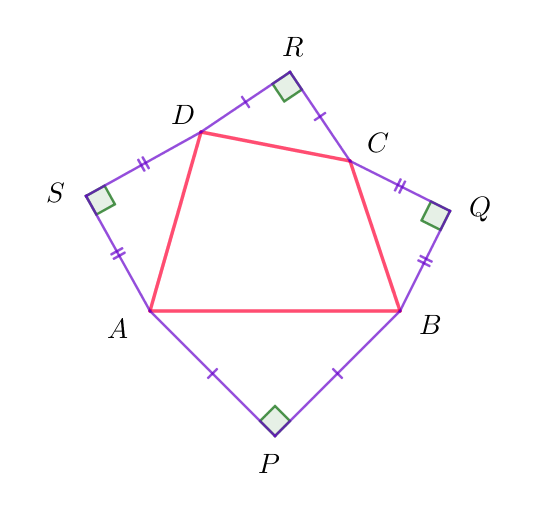
$\vec{PA}\ は \ \vec{PB}\ を点 \ P\ のまわりに \ 90°回転したものだから$
$\qquad \alpha -p=i(\beta -p)$
$\qquad (1-i)p=\alpha -i\beta$
\begin{eqnarray*}
p
&=&\cfrac{\alpha -i\beta}{1-i}\\
&=&\cfrac{1}{2}(\alpha -i\beta)(1+i)\\
&=&\cfrac{1}{2}\{\alpha + \beta +i(\alpha - \beta)\}\\
\end{eqnarray*}
(2)
$\vec{QB}\ は \ \vec{QC}\ を点 \ Q\ のまわりに、\vec{RC}\ は \ \vec{RD}\ を点 \ R\ のまわりに、\vec{SD}\ は \ \vec{SA}\ を点 \ S\ のまわりに$
$それぞれ \ \ 90°回転したものだから$
$(1)より \quad p=\cfrac{\alpha -i\beta}{1-i},\quad q=\cfrac{\beta -i\gamma}{1-i},\quad r=\cfrac{\gamma -i\delta}{1-i},\quad s=\cfrac{\delta -i\alpha}{1-i}$
$四角形PQRSが平行四辺形ならば \quad \vec{PQ}=\vec{SR} \qquad \therefore \ \ q-p=r-s $
$上の式を代入して$
$\cfrac{\beta -i\gamma}{1-i}-\cfrac{\alpha -i\beta}{1-i}=\cfrac{\gamma -i\delta}{1-i}-\cfrac{\delta -i\alpha}{1-i}$
$(\beta -i\gamma)-(\alpha -i\beta)=(\gamma -i\delta)-(\delta -i\alpha)$
$\alpha - \beta +i(\alpha - \beta)+\gamma -\delta +i(\gamma -\delta)=0$
$(1+i)(\alpha - \beta)+(1+i)(\gamma -\delta)=0$
$\alpha - \beta +\gamma -\delta =0$
$\alpha - \beta =\delta - \gamma$
$\vec{BA}=\vec{CD} \qquad よって 四角形ABCDは平行四辺形$
$逆をたどれるから、「四角形ABCDは平行四辺形」が必要十分条件である。$
(3)
$(2)より、四角形PQRSが平行四辺形ならば四角形ABCDは平行四辺形であるから$
$\quad \vec{BA}=\vec{CD} \quad より \quad \alpha - \beta =\delta - \gamma \quad \therefore \ \ \delta =\alpha -\beta +\gamma $
$また$
$(2)の \quad p=\cfrac{\alpha -i\beta}{1-i},\quad q=\cfrac{\beta -i\gamma}{1-i},\quad r=\cfrac{\gamma -i\delta}{1-i},\quad s=\cfrac{\delta -i\alpha}{1-i}\quad をつかって$
\begin{eqnarray*} s-p &=&\cfrac{\delta -i\alpha}{1-i}-\cfrac{\alpha -i\beta}{1-i}\\ &=&\cfrac{1}{1-i}(\delta -i\alpha -\alpha +i\beta)\\ &=&\cfrac{1}{1-i}((\alpha -\beta +\gamma )-i\alpha -\alpha +i\beta)\\ &=&\cfrac{1}{1-i}(-\beta +\gamma -i\alpha +i\beta)\\ \end{eqnarray*}
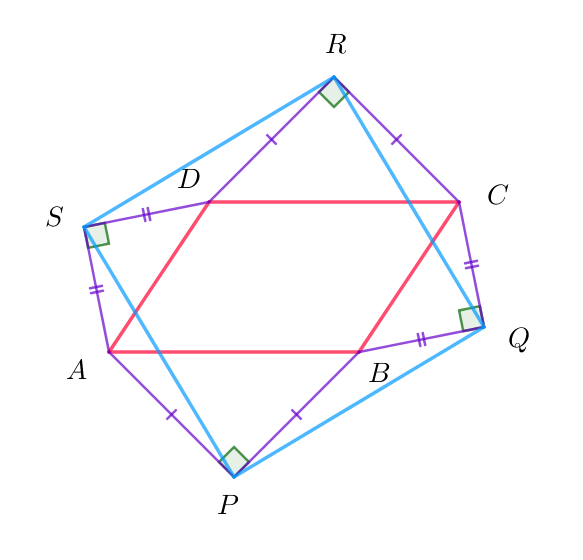
$また$
\begin{eqnarray*}
i(q-p)
&=&i\big(\cfrac{\beta -i\gamma}{1-i}-\cfrac{\alpha -i\beta}{1-i}\big)\\
&=&\cfrac{1}{1-i}(i\beta +\gamma -i\alpha -\beta)\\
&=&\cfrac{1}{1-i}(-\beta +\gamma -i\alpha +i\beta)\\
\end{eqnarray*}
$よって s-p=i(q-p)$
$\vec{PS}は\vec{PQ}を90°回転したものである。$
$四角形PQRSは平行四辺形で、かつ \ \ PQ=PS ,\ \ \angle QPS=90°\quad だから正方形である。$
$(研究)$
$この問題を定理に格上げし、幾何的に解いてみましょう。$
$定理 平行四辺形ABCDの外側に、各辺をそれぞれ斜辺とする直角二等辺三角形を作る。このとき$
$\hspace{3em} 4つの頂点を結んでできる四角形は正方形である。$
(i)
$直角二等辺三角形 ABP と直角二等辺三角形 CDR において$
$四角形ABCDは平行四辺形だから AB=CD$
$\angle BAP=\angle DCR=45°$
$\angle ABP=\angle CDR=45°$
$1辺と両端角が等しいので \triangle ABP \equiv \triangle CDR$
$よって AP=CR \hspace{10em}(1)$
$直角二等辺三角形 DAS と直角二等辺三角形 BCQ において$
$四角形ABCDは平行四辺形だから DA=BC$
$\angle ADS=\angle CBQ=45°$
$\angle DAS=\angle BCQ=45°$
$1辺と両端角が等しいので \triangle DAS \equiv \triangle BCQ$
$よって AS=CQ \hspace{10em}(2)$
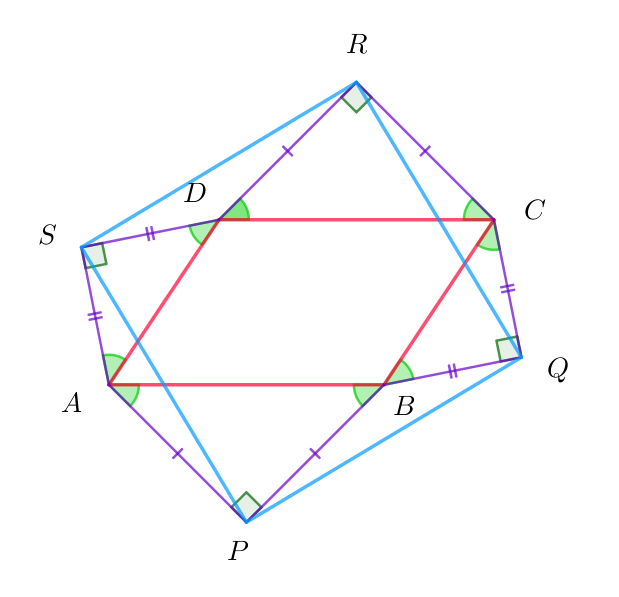
$\triangle APS と\triangle CRQ において$
$(1)より \quad AP=CR$
$(2)より \quad AS=CQ$
$\angle PAS=\angle PAB + \angle BAD +\angle DAS=45°+\angle BAD + 45°=90°+\angle BAD$
$また$
$\angle RCQ=\angle RCD + \angle DCB +\angle BCQ=45°+\angle DCB + 45°=90°+\angle DCB$
$四角形ABCDは平行四辺形だから \angle BAD=\angle DCB$
$よって \angle PAS=\angle RCQ \hspace{8em}(3)$
$(1),(2),(3)より、2辺とその間の角が等しいので \quad \triangle APS \equiv \triangle CRQ $
$よって \quad PS=RQ \hspace{10em}(4)$
(ii)
$\triangle PQB と\triangle RSD において$
$\triangle ABP \equiv \triangle CDR \quad より \quad BP=DR \hspace{4em}(5)$
$\triangle BCQ \equiv \triangle DAS \quad より \quad BQ=DS \hspace{4em}(6)$
$\angle PBQ=360°-\angle PBA - \angle ABC -\angle CBQ=360°-45°-\angle ABC - 45°=270°-\angle ABC$
$また$
$\angle RDS=360°-\angle RDC - \angle CBA -\angle ABS=360°-45°-\angle CBA - 45°=270°-\angle CBA$
$四角形ABCDは平行四辺形だから \angle ABC=\angle CBA$
$よって \angle PBQ=\angle RDS \hspace{10em}(7)$
$(5),(6),(7)より、2辺とその間の角が等しいので \quad \triangle PQB \equiv \triangle RSD $
$よって \quad PQ=RS \hspace{12em}(8)$
(iii)
$ \triangle BPQ と\triangle CRQ において$
$(5)より \quad BP=DR,\quad DR=CR \quad だから \quad BP=CR \hspace{3em}(9)$
$\triangle BCQ は直角二等辺三角形だから \quad BQ=CQ \hspace{6em}(10)$
$四角形ABCDは平行四辺形だから \angle ABC + \angle BCD=180°$
$\angle PBQ=360°-\angle PBA - \angle ABC -\angle CBQ=360°-45°- \angle ABC -45°=270°-\angle ABC$
$また$
$\angle QCR=\angle QCB + \angle BCD +\angle DCR=45°+\angle BCD +45°=90°+\angle BCD=90°+(180°-\angle ABC)=270°-\angle ABC$
$よって \quad \angle PBQ=\angle QCR \hspace{15em}(11)$
$(9),(10),(11)より、2辺とその間の角が等しいので \quad \triangle BPQ \equiv \triangle CRQ $
$\therefore PQ=RQ \hspace{10em}(12)$
$したがって (4),(8),(12)より、PQ=QR=RS=SP \quad となり四角形PQRS は正方形である。$
$おもしろい性質ですね。図形は奥が深いですね。!!$
メインメニュー に戻る