弘前大学(理系) 2024年　問題9


$i\ を虚数単位とする。次の問いに答えよ。$
$(1)\ \ 複素数平面上で、次の条件を満たす点 \ z\ はどのような図形をえがくか。$
$\hspace{5em} 条件 \ :\ \dfrac{(i-1)(z+2)}{iz} \ \ は実数である。$
$(2)\ \ 点 \ z\ が(1)の条件を満たしながら複素数平面上を動くとき、|iz-1|\ \ の最大値と最小値を求めよ。$


(1)


$\cfrac{(i-1)(z+2)}{iz} \ \ は実数だから$

$\cfrac{(i-1)(z+2)}{iz}=\overline{\Big(\dfrac{(i-1)(z+2)}{iz}\Big)}$

$\cfrac{(i-1)(z+2)}{iz}=\dfrac{(-i-1)(\overline{z}+2)}{-i\overline{z}}$

$\cfrac{(i-1)(z+2)}{iz}=\dfrac{(i+1)(\overline{z}+2)}{i\overline{z}}$

　

$(i-1)(z+2)\overline{z}=(i+1)(\overline{z}+2)z$

$i|z|^2+2i\overline{z}-|z|^2-2\overline{z}=i|z|^2+2iz+|z|^2+2z$

$|z|^2+(1+i)z+(1-i)\overline{z}=0$

$(z+1-i)(\overline{z}+1+i)=(1+i)(1-i)$

$(z+1-i)\overline{({z}+1-i)}=2$

$|z+1-i|=\sqrt{2}$

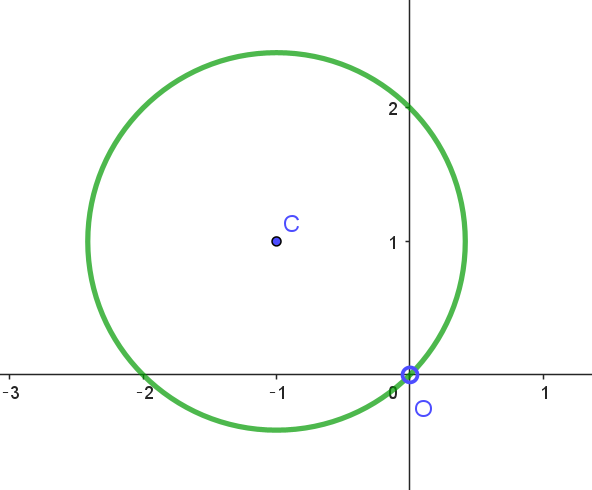
$よって\ \ z\ は \ \ 中心C(-1+i),\ \ 半径 \ \ \sqrt{2}\ \ の円をえがく。ただし \ \ z \ne 0$


(2)


$L=|iz-1|=|iz+i^2|=|i||z+i|=|z+i| \quad だから$

$L\ は点 \ z\ と点A(-i)\ の距離をあらわす。$

　

$(1)の円と直線ACの交点を右図のように \ B,\ D \ とおくと$

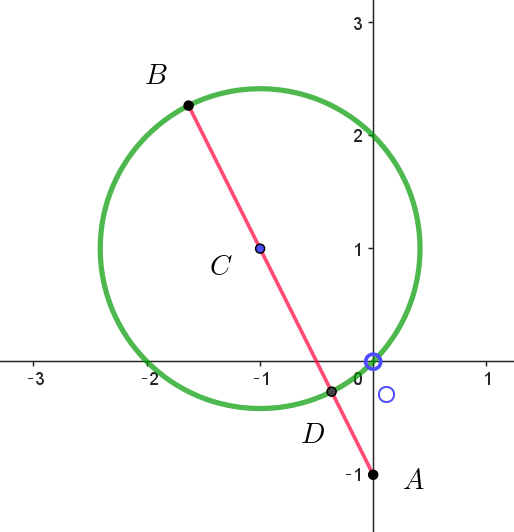
$点 \ z\ が(1)の円周上を動くとき、L\ の最大値は線分AB\ で、$

$最小値は \ AD\ である。$

$このとき、\vec{Az}=k\vec{AC}\ \ (k\ は実数)\ \ とおけるから$

$z+i=k((-1+i)+i)$

$z=-k+(2k-1)i$

$|z+1-i|=\sqrt{2} \ \ に代入して$

$|-k+(2k-1)i+1-i|=\sqrt{2} $

$|-(k-1)+2(k-1)i|=\sqrt{2} $

$|k-1||-1+2i|=\sqrt{2}$

$\sqrt{5}|k-1|=\sqrt{2}$

$|k-1|=\cfrac{\sqrt{2}}{\sqrt{5}}=\cfrac{\sqrt{10}}{5}$

$k-1=\pm \cfrac{\sqrt{10}}{5}$

$k=\cfrac{5 \pm \sqrt{10}}{5}$

$このとき$

$z+i=k(-1+2i)=\cfrac{5 \pm \sqrt{10}}{5}(-1+2i) \quad だから$

\begin{eqnarray*} L &=&|z+i|\\ \\ &=&\big|\cfrac{5 \pm \sqrt{10}}{5}(-1+2i)\big|\\ \\ &=&\big(\cfrac{5 \pm \sqrt{10}}{5}\big) \times \sqrt{5}\\ \\ &=&\cfrac{5 \pm \sqrt{10}}{\sqrt{5}}\\ \\ &=&\sqrt{5} \pm \sqrt{2}\\ \end{eqnarray*}
$よって、最大値は \ \ \sqrt{5} +\sqrt{2},\quad 最小値は \ \ \sqrt{5}-\sqrt{2}$

$なお、このときの \ z\ は、z=-k+(2k-1)i \quad だから$

$最大値は \quad z=-\cfrac{5 + \sqrt{10}}{5}+(2 \times \cfrac{5 \pm \sqrt{10}}{5} -1)i=-\cfrac{5 + \sqrt{10}}{5}+ \cfrac{5 +2\sqrt{10}}{5}i$

$最小値は \quad z=-\cfrac{5 - \sqrt{10}}{5}+(2 \times \cfrac{5 - \sqrt{10}}{5} -1)i=-\cfrac{5 - \sqrt{10}}{5}+ \cfrac{5 -2\sqrt{10}}{5}i$


ページの先頭へ↑



メインメニュー　に戻る