弘前大学(理系) 2024年 問題8
$関数 \ f(x)\ を \ \ f(x)=e^{\sqrt{2}\cos x} \sin x \ \ と定める。ただし、e\ は自然対数の底とする。次の問いに答えよ。$
$(1)\ \ 0 \leqq x \leqq 2\pi \ \ における \ f(x)\ の最大値と最小値を求めよ。また、そのときの \ x\ の値を求めよ。$
$(2)\ \ 0 \leqq x \leqq 2\pi \ \ の範囲において、曲線 \ y=f(x) \ と \ x\ 軸で囲まれた部分の面積を求めよ。$
(1)
$f(x)=e^{\sqrt{2}\cos x} \sin x \ \ の両辺の対数をとって$
$\log f(x)=\sqrt{2}\cos x + \log \sin x$
$両辺を微分して$
\begin{eqnarray*} \cfrac{f'(x)}{f(x)} &=&-\sqrt{2}\sin x + \cfrac{\cos x}{\sin x}\\ \\ &=&\cfrac{-\sqrt{2}\sin ^2x + \cos x}{\sin x}\\ \\ &=&\cfrac{-\sqrt{2}(1-\cos ^2x) + \cos x}{\sin x}\\ \\ &=&\cfrac{\sqrt{2}\cos ^2x + \cos x-\sqrt{2}}{\sin x}\\ \\ &=&\cfrac{(\sqrt{2}\cos x -1)(\cos x +\sqrt{2})}{\sin x}\\ \end{eqnarray*}
$\therefore \ \ f'(x)=(\sqrt{2}\cos x -1)(\cos x +\sqrt{2})e^{\sqrt{2}\cos x}$
$f'(x)=0 \quad より \quad \cos x=\cfrac{1}{\sqrt{2}}$
$0 \leqq x \leqq 2\pi \ \ の範囲で \quad x=\cfrac{\pi}{4},\quad \cfrac{7}{4}\pi$
\[ \begin{array}{c||c|c|c|c|c} x& 0 & \cdots & \dfrac{\pi}{4} & \cdots & \dfrac{7}{4}\pi & \cdots & 2\pi\\ \hline f'(x) & & + & 0 & - & 0 & + & \\ \hline f(x)& 0 & \nearrow & 極大 & \searrow & 極小 & \nearrow & 0\\ \end{array} \]
$f(0)=0,\quad f(2\pi)=0,\quad f(\dfrac{\pi}{4})=\cfrac{e} {\sqrt{2}},\quad f(\dfrac{7}{4}\pi)=-\cfrac{e}{\sqrt{2}}$
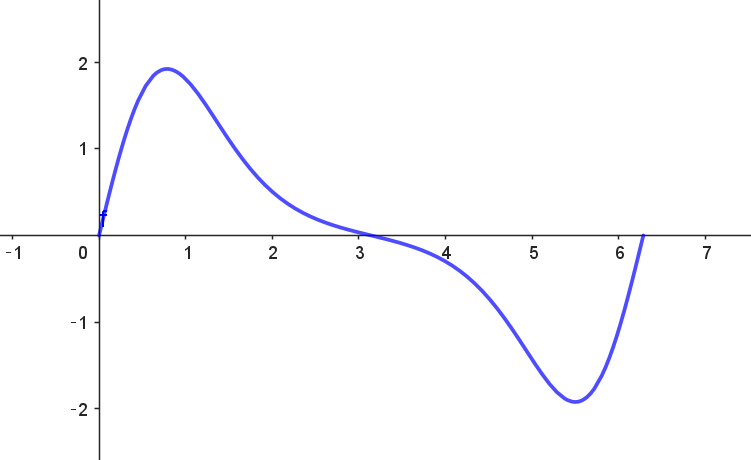
$x=\dfrac{\pi}{4}\ \ で極大かつ最大となり、最大値は\ \ f(\dfrac{\pi}{4})=\cfrac{e}{\sqrt{2}}$
$x=\dfrac{7}{4}\pi\ \ で極小かつ最小となり、最小値は\ \ f(\dfrac{7}{4}\pi)=-\cfrac{e}{\sqrt{2}}$
$(補充)$
$y=f(x)\ のグラフは右図のとおりであるが、点(\pi, \ 0)\ \ に関して点対称である。$
$(証明)$
$y=f(x)\ 上の点P(x,\ y)\ の点(\pi,\ 0)に関する対称点を \ (u,\ v)\ とおくと$
$\cfrac{x+u}{2}=\pi,\quad \cfrac{y+v}{2}=0$
$x=2\pi - u, \quad y=-v$
$y=e^{\sqrt{2}\cos x} \sin x \ \ に代入して$
$-v=e^{\sqrt{2}\cos (2\pi-u)} \sin (2\pi -u)$
$-v=e^{\sqrt{2}\cos ux}(- \sin u)$
$v=e^{\sqrt{2}\cos ux}\sin u$
$したがって \quad 点(u,\ v)\ は \ y=f(x)\ 上の点である。$
(2)
$求める部分の面積を \ S\ とおくと$
\begin{eqnarray*} S &=&\int_0^{\pi}e^{\sqrt{2}\cos x} \sin x dx -\int_{\pi}^{2\pi}e^{\sqrt{2}\cos x} \sin x dx\\ \\ & & \qquad \cos x=t \ \ とおくと \ \ -\sin x dx=dt\\ \\ &=&\int_1^{-1}e^{\sqrt{2}t} (-dt) -\int_{-1}^1e^{\sqrt{2}t}(-dt)\\ \\ &=&\int_{-1}^1e^{\sqrt{2}t}dt +\int_{-1}^1 e^{\sqrt{2}t}dt\\ \\ &=&2\int_{-1}^1e^{\sqrt{2}t}dt \\ \\ &=&\cfrac{2}{\sqrt{2}}\big[e^{\sqrt{2}t}\big]_{-1}^1 \\ \\ &=&\sqrt{2}\big(e^{\sqrt{2}}-e^{-\sqrt{2}}\big)\\ \end{eqnarray*}
$(注意)$
$(1)の補充で示したように、対称性を用いれば定積分は半分ですみます。$
メインメニュー に戻る