弘前大学(理系) 2024年 問題7
$a,\ b,\ c\ を実数とする。座標空間において、4\ 点 \ O(0,\ 0,\ 0),\ P(2,\ 0,\ a),\ Q(0,\ b,\ c),\ R(1,\ 2,\ 2)\ がある。$
$ただし、点Q\ は点O\ とは異なる。次の問いに答えよ。$
$(1)\ \ \cos \angle POQ \ \ を \ a,\ b,\ c\ を用いて表せ。$
$(2)\ \ 3\ 点 \ P,\ Q,\ R\ が一直線上にあるための \ a,\ b,\ c\ の条件を求めよ。$
$(3)\ \ 3\ 点 \ P,\ Q,\ R\ が一直線上にあるように点P,\ Q\ が動くとき、三角形OPQ\ の面積の最小値を求めよ。$
(1)
$\triangle PQR に余弦定理を用いて$
\begin{eqnarray*} & &\cos \angle POQ\\ \\ &=&\cfrac{OP^2+OQ^2-PQ^2}{2OP \cdot OQ}\\ \\ &=&\cfrac{(4+a^2)+(b^2+c^2)-(4+b^2+(a-c)^2)}{2\sqrt{4+a^2}\cdot \sqrt{b^2+c^2}}\\ \\ &=&\cfrac{ac}{\sqrt{4+a^2}\cdot \sqrt{b^2+c^2}}\\ \end{eqnarray*}
(2)
$3\ 点 \ P,\ Q,\ R\ が一直線上にあるための条件は$
$\vec{PQ}=k\vec{PR}\ \ (k\ は実数)\ \ が成りたつことだから$
$\vec{OQ}-\vec{OP}=k(\vec{OR}-\vec{OP})$
$(0,\ b,\ c)-(2,\ 0,\ a)=k\big((1,\ 2,\ 2)-(2,\ 0,\ a)\big)$
$(-2,\ b,\ c-a)=k(-1,\ 2,\ 2-a)$
\[ \hspace{1em} \left\{ \begin{array}{l} -2=-k \hspace{5.5em}①\\ b=2k \hspace{6.7em}②\\ c-a=k(2-a) \hspace{2.5em}③\\ \end{array} \right. \]
$①より \quad k=2$
$②に代入して \quad b=4$
$③に代入して \quad c-a=2(2-a) \qquad a+c=4$
$よって、3\ 点 \ P,\ Q,\ R\ が一直線上にあるための \ a,\ b,\ c\ の条件は \quad a+c=4,\ \ b=4$
(3)
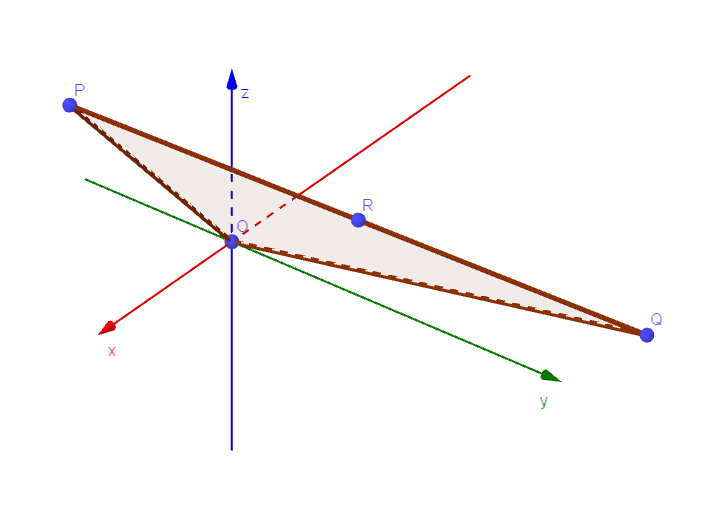
$点R\ は線分PQ\ の中点である。$
$したがって \quad \triangle OPQ\ の面積 \ S=2(\triangle OPR の面積)$
$\angle POR=\theta \ \ とおくと \ \ \cos \theta=\cfrac{\vec{OP}\cdot \vec{OR}}{|\vec{OP}||\vec{OR}|} \ \ だから$
\begin{eqnarray*} S &=&2\triangle OPR\\ \\ &=&2 \times \cfrac{1}{2} \times |\vec{OP}||\vec{OR}|\sin \theta\\ \\ &=&|\vec{OP}||\vec{OR}|\sqrt{1-\cos ^2 \theta}\\ \\ &=&|\vec{OP}||\vec{OR}|\sqrt{1-\cfrac{(\vec{OP}\cdot \vec{OR})^2}{|\vec{OP}|^2|\vec{OR}|^2}}\\ \\ &=&\sqrt{|\vec{OP}|^2|\vec{OR}|^2-(\vec{OP}\cdot \vec{OR})^2}\\ \\ &=&\sqrt{(4+a^2)\times 9 -(2+2a)^2}\\ \\ &=&\sqrt{5a^2-8a+32}\\ \\ &=&\sqrt{5(a-\dfrac{4}{5})^2+\dfrac{144}{5}}\\ \end{eqnarray*}
$よって、三角形OPQ\ の面積 \ S\ の最小値は \quad a=\cfrac{4}{5} \ \ のとき \ \ S=\sqrt{\dfrac{144}{5}}=\cfrac{12\sqrt{5}}{5}$
$なおこのとき、P(2,\ 0,\ \dfrac{4}{5}),\ \ Q(0,\ 4,\ \dfrac{16}{5})\ \ である。$
メインメニュー に戻る