弘前大学(理系) 2024年　問題6


$何も入っていない \ 2\ つの箱 \ A,\ B\ と \ 1\ 個の球がある。はじめに球を箱 \ A\ に入れて、1\ 個のさいころを \ 1\ 回$
$投げるごとに以下の規則に従って球を操作する。$
$\bullet \ \ 球が箱 \ A\ に入っているとき、さいころの出た目が \ 1\ から \ 4\ までのいずれかであれば球を箱 \ A\ から箱 \ B$
$\quad に移動させ、さいころの出た目が \ 5,\ 6\ のいずれかであれば球を箱 \ A\ から動かさない。$
$\bullet \ \ 球が箱 \ B\ に入っているとき、さいころの出た目が \ 1\ から \ 5\ までのいずれかであれば球を箱 \ B\ から箱 \ A$
$\quad に移動させ、さいころの出た目が \ 6\ であれば球を箱 \ B\ から動かさない。$
$n\ を自然数とし、さいころを \ n\ 回投げて球の操作を終えた時点で球が箱 \ A\ に入っている確率を \ a_n \ とする。$
$次の問いに答えよ。$
$(1)\ \ a_1,\ \ a_2\ \ を求めよ。$
$(2)\ \ a_{n+1}\ を \ a_n \ を用いて表せ。$
$(3)\ \ a_n \ を求めよ。$


(1)


$さいころを \ 1\ 回投げて、球が箱 \ A\ に入っている事象は球が移動しない場合だから$

$a_1=\cfrac{2}{6}=\cfrac{1}{3}$

　

$右の樹形図より$

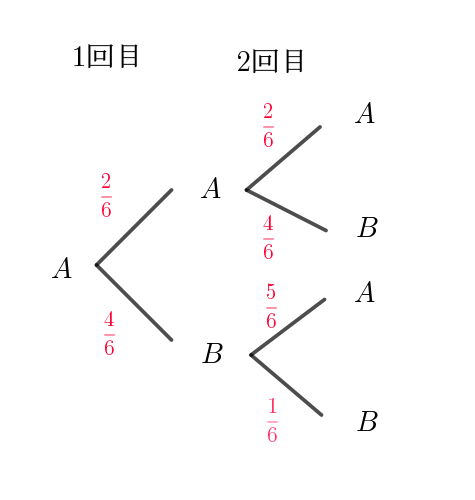
$a_2=\cfrac{2}{6} \times \cfrac{2}{6}+\cfrac{4}{6} \times \cfrac{5}{6}=\cfrac{24}{36}=\cfrac{2}{3}$


(2)


$さいころを \ n\ 回投げて球が箱 \ A\ に入っている事象の確率が\ a_n \ ならば$

$箱 \ B\ に入っている事象の確率はその余事象だから \quad 1-a_n \ $

$(n+1)\ 回投げて球が箱 \ A\ に入っている事象の確率\ a_{n+1} \ は$

$この樹形図は右のとおりで$

　

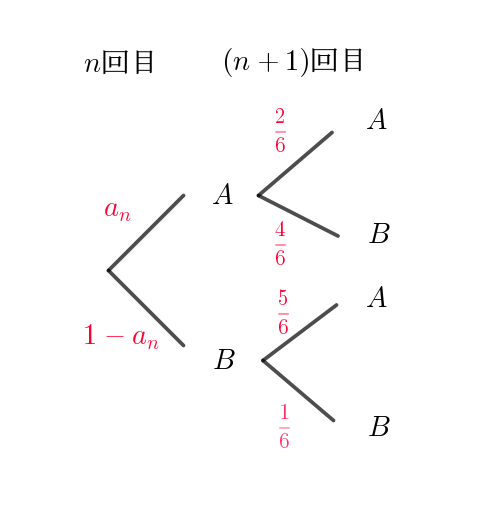
$a_{n+1}=a_n \times \cfrac{2}{6}+(1-a_n) \times \cfrac{5}{6}$

$a_{n+1}=-\cfrac{1}{2}a_n + \cfrac{5}{6}$


(3)


$a_{n+1}=-\cfrac{1}{2}a_n + \cfrac{5}{6}$

$この漸化式の特性方程式は$

$t=-\cfrac{1}{2}t+\cfrac{5}{6} \quad より \quad t=\cfrac{5}{9}$

$辺々引いて$

$a_{n+1}-\cfrac{5}{9}=-\cfrac{1}{2}\big(a_n-\cfrac{5}{9}\big)$
\begin{eqnarray*} a_n-\cfrac{5}{9} &=&\big(-\dfrac{1}{2}\big)^{n-1}\big(a_1-\dfrac{5}{9}\big)\\ \\ &=&\big(-\dfrac{1}{2}\big)^{n-1}\big(\dfrac{1}{3}-\dfrac{5}{9}\big)\\ \\ &=&-\cfrac{2}{9}\big(-\dfrac{1}{2}\big)^{n-1}\\ \end{eqnarray*} $\therefore\ \ a_n=\cfrac{5}{9} -\cfrac{2}{9}\big(-\dfrac{1}{2}\big)^{n-1}$


ページの先頭へ↑



メインメニュー　に戻る