弘前大学(理系) 2024年　問題5


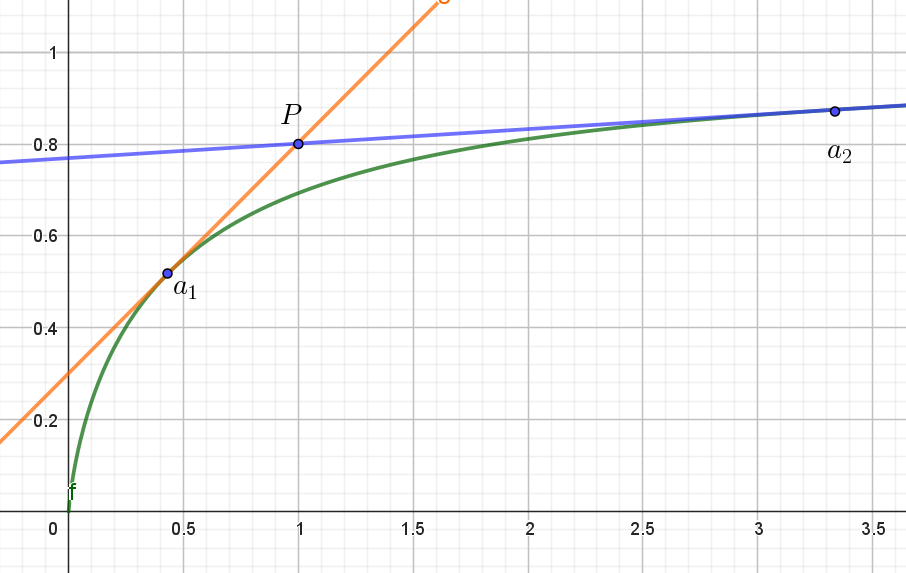
$x > 0\ に\ おいて、関数 \ f(x)\ を \ \ f(x)=x\log (1+\dfrac{1}{x}) \ \ と定める。また、a\ を正の実数とし、曲線 \ y=f(x)\ 上の$
$点(a,\ f(a))\ における接線を \ \ell _a \ とする。次の問いに答えよ。$
$(1)\ \ 直線 \ \ell _a \ の方程式を求めよ。$
$(2)\ \ 直線 \ \ell _a \ が点(1,\ \dfrac{4}{5})\ を通るような \ a\ はいくつあるか。必要ならば \ \ \log 2 < 0.7 \ \ であることを用いてよい。$


(1)

　

$f(x)=x\log (1+\dfrac{1}{x}) \ \ より$
\begin{eqnarray*} f'(x) &=&\log (1+\dfrac{1}{x})+x \times \cfrac{-\dfrac{1}{x^2}}{1+\dfrac{1}{x}}\\ \\ &=&\log (1+\dfrac{1}{x}) -\cfrac{1}{x+1}\\ \end{eqnarray*}
$点(a,\ f(a))\ における接線\ \ell _a \ は$

$y-a\log (1+\dfrac{1}{a})=\big(\log (1+\dfrac{1}{a}) -\cfrac{1}{a+1}\big)(x-a)$

$\therefore \ \ \ell_a : y=\big(\log (1+\dfrac{1}{a}) -\cfrac{1}{a+1}\big)x + \cfrac{a}{a+1}$


(2)


$\ell_a \ が点(1,\ \dfrac{4}{5})\ \ を通るから$

$\big(\log (1+\dfrac{1}{a}) -\cfrac{1}{a+1}\big) + \cfrac{a}{a+1}=\cfrac{4}{5}$

$\log (1+\dfrac{1}{a}) + \cfrac{a-1}{a+1}=\cfrac{4}{5}$

$\log (1+\dfrac{1}{a}) + \big(1-\cfrac{2}{a+1}\big)=\cfrac{4}{5}$

$\log (a+1)-\log a -\cfrac{2}{a+1} + \cfrac{1}{5} =0$

$g(a)=\log (a+1)-\log a -\cfrac{2}{a+1} + \cfrac{1}{5} \quad とおくと$
\begin{eqnarray*} g'(a) &=&\cfrac{1}{a+1} -\cfrac{1}{a} + \cfrac{2}{(a+1)^2}\\ \\ &=&\cfrac{a(a+1)-(a+1)^2+2a}{a(a+1)^2}\\ \\ &=&\cfrac{a-1}{a(a+1)^2}\\ \end{eqnarray*} $g'(a)=0 \ \ より \quad a=1$

$増減表$
\[ \begin{array}{c||c|c|c|c|c} a& 0 & \cdots & 1 & \cdots \\ \hline g'(a) & & - & 0 & + \\ \hline g(a)& & \searrow & 極小 & \nearrow & \\ \end{array} \]
$a=1\ で極小かつ最小となり、最小値は$

$g(1)=\log 2 -1+\cfrac{1}{5}=\log 2 -\cfrac{4}{5}< 0.7-0.8=-0.1$

$a \longrightarrow +0 \ \ のとき \quad g(a) \longrightarrow +\infty$

$a \longrightarrow +\infty \ \ のとき \quad g(a) \longrightarrow \cfrac{1}{5}$

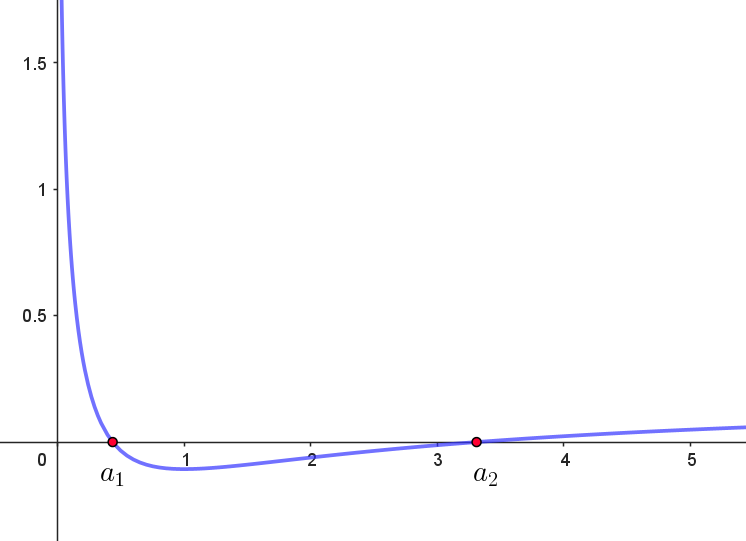
$g(a)\ のグラフは \ a\ 軸と \ 2\ 点で交わるから、直線 \ \ell _a \ が点(1,\ \dfrac{4}{5})\ を通るような \ a\ は \ 2\ つある。$

　

$(補充)$

$中間値の定理より$

$a \longrightarrow +0 \ \ のとき \quad g(a) \longrightarrow +\infty, \quad g(1) < 0\ \ だから$

$ 0 < a_1 < 1 $

$関数電卓を用いて計算すると$

$g(3)=\log 4-\log 3-\cfrac{1}{2}+\cfrac{1}{5}=\log \dfrac{4}{3}-\cfrac{3}{10}=0.287-0.3<0$

$g(4)=\log 5-\log 4-\cfrac{2}{5}+\cfrac{1}{5}=\log \dfrac{5}{4}-\cfrac{1}{5}=0.223-0.2>0$

$よって \quad 3 < a_2 < 4$

$なお、グラフ作成ソフトを使って描いたグラフは右図のとおりである。$


ページの先頭へ↑



メインメニュー　に戻る