群馬大学(理系) 2024年　問題6


$f(x)=x\log(1+x) \ とおく。ただし、\log x \ は \ x\ の自然対数を表す。以下の問に答えよ。$
$(1)\ \ 曲線 \ y=f(x)\ 上の点(0,\ 0)\ における接線の方程式を求めよ。$
$(2)\ \ 関数 \ f(x)\ の増減を調べ、極値を求めよ。$
$(3)\ \ 直線 \ y=x\ と曲線 y=f(x)\ で囲まれた部分の面積を求めよ。$


(1)

$f(x)=x\log(1+x) \quad より \quad f'(x)=\log(1+x)+\cfrac{x}{1+x}$

$f'(0)=0 , \quad f(0)=0 \quad だから$

$点(0,\ 0)\ における接線の方程式は \quad y=0$


(2)

　

$f'(x)=\log(1+x)+\cfrac{x}{1+x} \quad において$

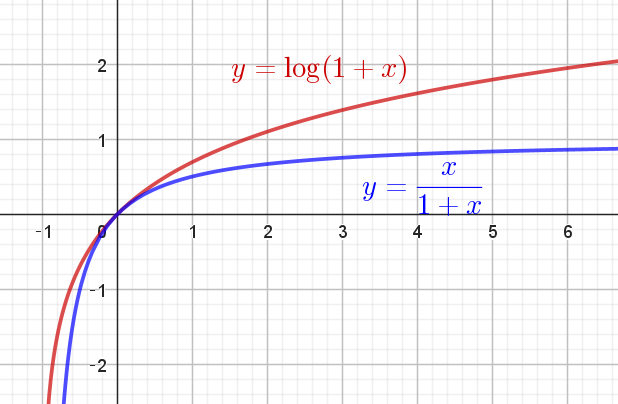
$y=\log (1+x)\ \ と \ \ y=\cfrac{x}{1+x}=1-\cfrac{1}{1+x} \ \ はともに$

$-1 < x < 0 \ \ のとき \ \ y < 0$

$x=0 \ \ のとき \ \ y=0$

$x > 0 \ \ のとき \ \ y > 0$

$したがって増減表は$

　

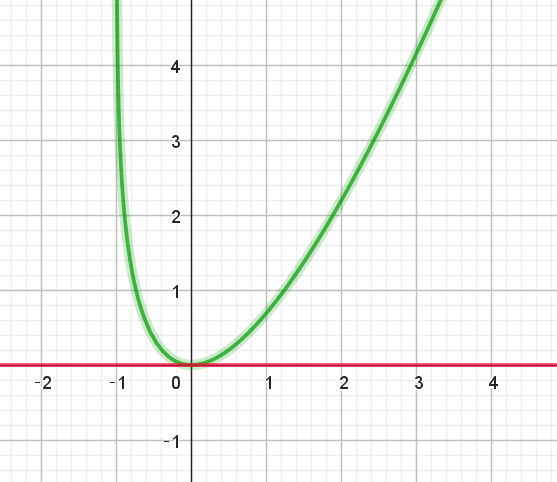
\[ \begin{array}{c||c|c|c|c|c} x& -1 & \cdots & 0 & \cdots \\ \hline f'(x) & & - & 0 & + & \\ \hline f(x) & & \searrow & 極小 & \nearrow & \\ \end{array} \] $x=0 \ \ のとき極小となり極小値は \quad f(0)=0$

$このことから \ \ y=f(x)\ のグラフは右図のとおりである。$

$なお、(1)で点(0,\ 0)\ における接線の方程式は \ y=0\ であったので$

$グラフでは、赤い直線で示してある。$


(3)

　

$y=x \ と \ y=f(x)\ の交点の \ x\ 座標は$

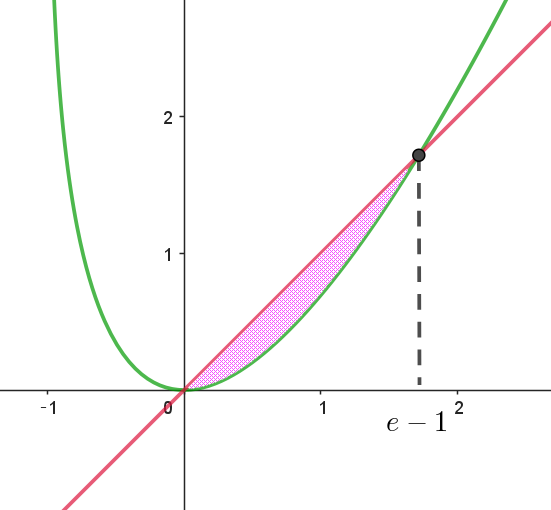
$x\log(1+x)=x　\qquad x(\log(1+x)-1)=0$

$x=0,\quad \log(1+x)=1 \ \ より \ \ x=e-1$

$y=x\ と \ y=f(x)\ で囲まれた部分の面積 \ S\ は$

\begin{eqnarray*} S &=&\int_0^{e-1} (x-x\log(1+x))dx\\ \\ &=&\int_0^{e-1} x(1-\log(1+x))dx\\ \\ &=&\big[\dfrac{x^2}{2}(1-\log(1+x))\big]_0^{e-1} -\int_0^{e-1} \dfrac{x^2}{2}(-\dfrac{1}{1+x})dx\\ \\ &=&\cfrac{1}{2}\int_0^{e-1} \dfrac{x^2}{1+x}dx\\ \\ &=&\cfrac{1}{2}\int_0^{e-1} \big(x-1+\dfrac{1}{1+x}\big)dx\\ \\ &=&\cfrac{1}{2}\big[\dfrac{x^2}{2}-x+\log(1+x)\big]_0^{e-1}\\ \\ &=&\cfrac{1}{2}\big\{\dfrac{1}{2}(e-1)^2-(e-1)+1\big\}\\ \\ &=&\cfrac{1}{4}(e^2-4e+5) \end{eqnarray*}

ページの先頭へ↑




メインメニュー　に戻る