群馬大学(理系) 2024年　問題5


$xy平面上において、連立不等式 \ \ y \leqq -x^2+4x , \ \ 2x+y \geqq 0 \ \ の表す領域を \ A\ とする。以下の問に答えよ。$
$(1)\ \ 領域 \ A\ の面積を求めよ。$
$(2)\ \ 点(x,\ y)\ が領域 \ A\ を動くとき、\dfrac{y+11}{x+6} の最大値と最小値を求めよ。$


(1)

　

$領域 \ A\ は右図のとおり$

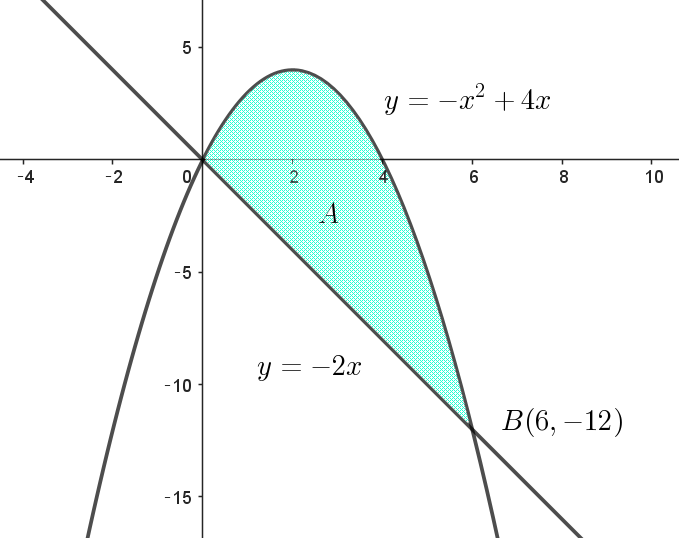
$y=-x^2+4x\ と \ y=-2x \ の交点の \ x\ 座標は$

$-x^2+4x=-2x$

$x(x-6)=0$

$x=0,\ \ 6$

$領域 \ A\ の面積 \ S\ は$
\begin{eqnarray*} S &=&\int_0^6\big(-x^2+4x-(-2x)\big)dx\\ \\ &=&\int_0^6(-x^2+6x)dx\\ \\ &=&\big[-\dfrac{1}{3}x^3+3x^2\big]_0^6\\ \\ &=&-\cfrac{6^3}{3}+3 \times 6^2\\ \\ &=&36 \end{eqnarray*}

(2)

　

$\cfrac{y+11}{x+6}=k \quad とおくと$

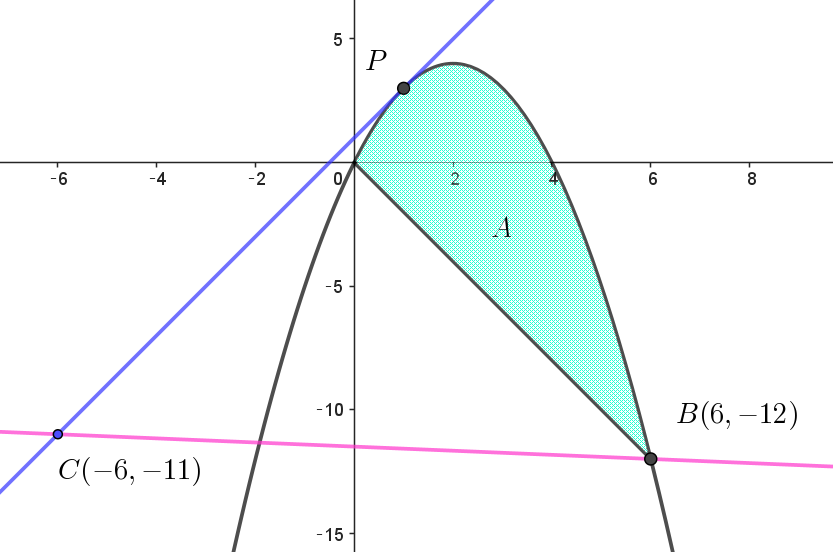
$y=k(x+6)-11$

$これは、点B(-6,-11)\ を通る傾き \ k\ の直線を表している。$

$領域 \ A\ を通るこの直線の傾きの最大値と最小値を$

$求めればよい。$

(i)$\ \ 最大値$

$\quad y=-x^2+4x とy=k(x+6)-11 \ \ が接するとき \ k\ は最大となる。$

$\quad -x^2+4x=k(x+6)-11$

$\quad x^2+(k-4)x+6k-11=0$

$\quad 接する条件は$

$\quad D=(k-4)^2-4(6k-11)=0$

$\quad k^2-32k+60=0$

$\quad (k-2)(k-30)=0$

$\quad k=2,30$

$\quad このとき、接点の \ x\ 座標は \quad x=-\cfrac{k-4}{2} \quad だから$

$\quad k=2 \ \ のとき \ \ x=1 \quad このとき \ \ y=3$

$\quad k=30 \ \ のとき \ \ x=-13 \quad これは領域 \ A\ の範囲外である。$

$\quad したがって 点P(1,\ 3)\ \ のとき \ k\ は最大値 \ 2\ をとる。$

(ii)$\ \ 最小値$

$\quad 点B(6,-12)\ を通るとき \ k\ は最小となる。$

$\quad このとき \quad k=\cfrac{-12+11}{6+6}=-\cfrac{1}{12}$


ページの先頭へ↑




メインメニュー　に戻る