群馬大学(理系) 2024年　問題4


$1\ 辺の長さが \ \sqrt{2}\ の正四面体 \ OABC\ がある。辺 \ AB\ を \ t:(1-t)\ に内分する点を \ P,辺 \ BC\ を \ t^2:(1-t^2)\ に$
$内分する点を \ Q\ とする。ただし、t\ は \ 0< t < 1\ を満たす実数とする。以下の問に答えよ。$
$(1)\ \ 内積 \ \vec{OP}\cdot \vec{OQ}\ を \ t\ を用いて表せ。$
$(2)\ \ 内積 \ \vec{OP}\cdot \vec{OQ}\ の最大値と、そのときの実数 \ t\ の値を求めよ。$


(1)

　

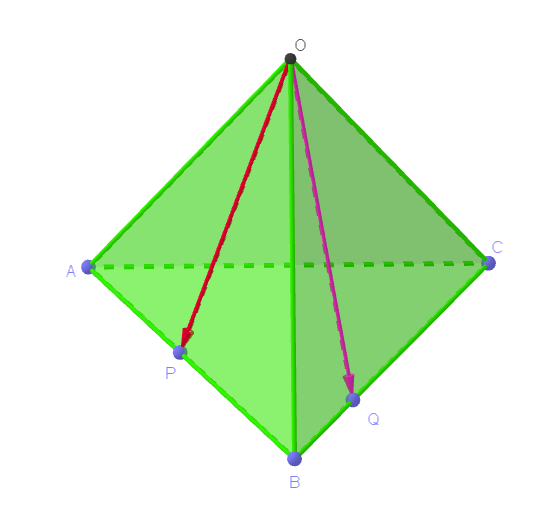
$\vec{OA}=\vec{a},\quad \vec{OB}=\vec{b} ,\quad \vec{OC}=\vec{c} \quad とおくと$

$正四面体 \ OABC\ の各面は、1\ 辺の長さが \ \sqrt{2}\ の正三角形だから$

$\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|\cos \dfrac{\pi}{3}=\sqrt{2} \times \sqrt{2} \times \cfrac{1}{2}=1$

$同様にして \quad \vec{b} \cdot \vec{c}=1,\quad \vec{c}\cdot \vec{a}=1$

$\vec{OP}=(1-t)\vec{a}+t\vec{b} $

$\vec{OQ}=(1-t^2)\vec{b}+t^2\vec{c} $

$このとき$
\begin{eqnarray*} & &\vec{OP}\cdot \vec{OQ}\\ \\ &=&\big\{(1-t)\vec{a}+t\vec{b}\big\} \cdot \big\{(1-t^2)\vec{b}+t^2\vec{c}\big\}\\ \\ &=&(1-t)(1-t^2)\vec{a}\cdot \vec{b} + (1-t)t^2\vec{a} \cdot \vec{c} + t(1-t^2)|\vec{b}|^2+t^3\vec{b} \cdot \vec{c}\\ \\ &=&(1-t)(1-t^2) + (1-t)t^2 + 2t(1-t^2)+t^3\\ \\ &=&-t^3+t+1 \end{eqnarray*}

(2)


$(1)より \quad \vec{OP}\cdot \vec{OQ}=-t^3+t+1 \quad だから$

$f(t)=-t^3+t+1 \ \ (0 < t < 1) \ \ とおくと$
　
$f'(t)=-3t^2+1=-3(t^2-\cfrac{1}{3})$

$f'(t)=0 \ \ より \ \ t=\cfrac{1}{\sqrt{3}}$

　

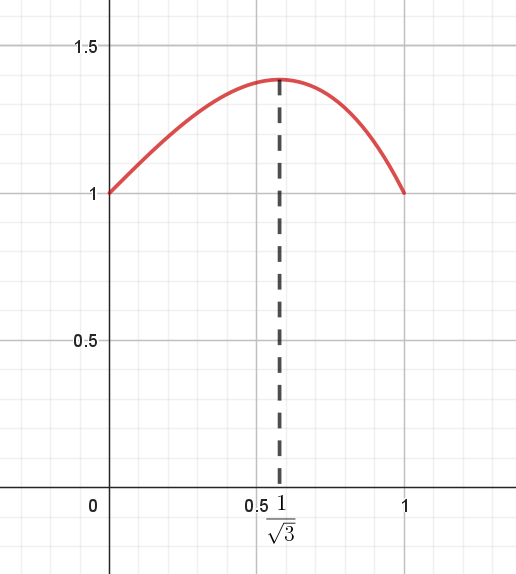
\[ \begin{array}{c||c|c|c|c|c} t& 0 & \cdots & \dfrac{1}{\sqrt{3}} & \cdots & 1\\ \hline f'(t)& & + & 0 & - & \\ \hline f(t)& & \nearrow & 極大 & \searrow & \\ \end{array} \]
$t=\cfrac{1}{\sqrt{3}}\ で \ f(t)\ は極大かつ最大となり、最大値は$

$f\big(\cfrac{1}{\sqrt{3}}\big)=-\cfrac{1}{3\sqrt{3}} + \cfrac{1}{\sqrt{3}} +1= -\cfrac{\sqrt{3}}{9}+ \cfrac{\sqrt{3}}{3}+1=1+\cfrac{2\sqrt{3}}{9}$

$なお、f(t)\ のグラフは右図のとおり$



ページの先頭へ↑




メインメニュー　に戻る