群馬大学(理系) 2024年　問題2


$a,\ b,\ c\ を実数の定数とする。x\ についての整式 \ A(x)\ と \ B(x)\ を$
$\quad A(x)=x^3-3ax^2+3bx+c ,\quad B(x)=x^2-2ax+b$
$とおく。3\ 次方程式 \ A(x)=0 \ は \ x=-1\ を解にもつとし、A(x)\ を \ x+1 \ で割った商を \ Q(x)\ とする。$
$以下の問に答えよ。$
$(1)\ \ Q(x)\ を求めよ。また、c\ を \ a\ と \ b\ を用いて表せ。$
$(2)\ \ 方程式 \ Q(x)=0\ が実数解をもつとき、方程式 \ B(x)=0 \ も実数解をもつことを示せ。$
$(3)\ \ 2\ つの方程式 \ Q(x)=0,\ \ B(x)=0\ がともに \ x=a+1\ を解にもつとき、定数 \ a\ の値を求めよ。$


(1)


$A(x)=0 \ は \ x=-1\ を解にもつから \ \ x+1 \ は \ A(x)\ の因数である。$

$A(x)\ を \ x+1 \ で割った商が \ Q(x)\ だから \ \ A(x)=(x+1)Q(x) \ \ とおける。$

　

$右のように筆算の割り算を行うと$

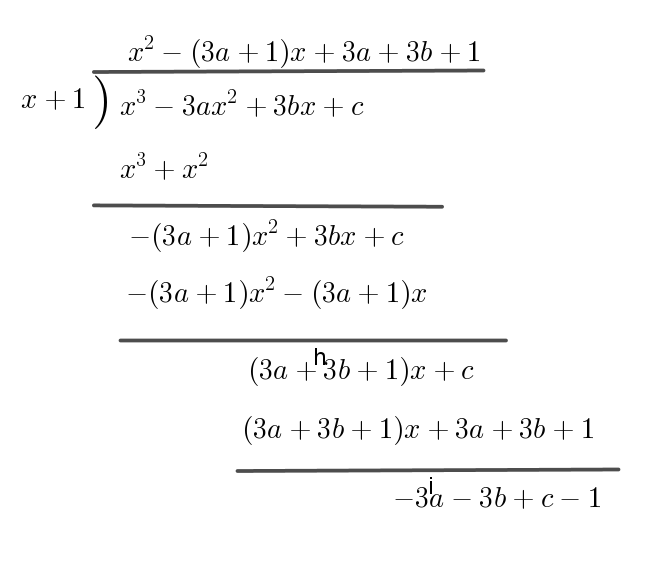
$A(x)\ を \ x+1\ で割った商\ Q(x)\ は$

$Q(x)=x^2-(3a+1)x+3a+3b+1$

$割り切れるから余りは \ 0$

$-3a-3b+c-1=0$

$\therefore \ \ c=3a+3b+1$


(2)


$Q(x)=x^2-(3a+1)x+3a+3b+1=0 \ \ が実数解をもつならば$

$D=(3a+1)^2-4(3a+3b+1) \geqq 0$

$9a^2-6a-12b-3 \geqq 0$

$\therefore \ \ -b \geqq -\cfrac{3}{4}a^2+ \cfrac{1}{2}a +\cfrac{1}{4}$

$このとき \quad B(x)=x^2-2ax+b=0 \quad の判別式は$

\begin{eqnarray*} \cfrac{D}{4} &=&a^2-b\\ \\ &\geqq& a^2 -\cfrac{3}{4}a^2+ \cfrac{1}{2}a +\cfrac{1}{4}\\ \\ &=&\cfrac{1}{4}a^2+ \cfrac{1}{2}a +\cfrac{1}{4}\\ \\ &=&\cfrac{1}{4}(a^2+ 2a + 1)\\ \\ &=&\cfrac{1}{4}(a + 1)^2\\ \\ &\geqq&0 \end{eqnarray*} $よって \quad B(x)=0 \ \ は実数解をもつ$


(3)


$B(x)=0 \ は\ x=a+1\ を解にもつから$

$B(a+1)=(a+1)^2-2a(a+1)+b=0$

$b=a^2-1 \hspace{5em}①$

$Q(x)=x^2-(3a+1)x+3a+3b+1=(x^2-2ax+b)-(a+1)x+3a+2b+1=B(x)-(a+1)x+3a+2b+1$

$Q(x)=0 \ も\ x=a+1\ を解にもつから$

$Q(a+1)=B(a+1)-(a+1)^2+3a+2b+1=0$

$-(a+1)^2+3a+2b+1=0$

$-a^2+a+2b=0$

$①を代入して$

$-a^2+a+2(a^2-1)=0$

$a^2+a-2=0$

$(a-1)(a+2)=0$

$\therefore \ \ a=1,\ \ -2$


ページの先頭へ↑




メインメニュー　に戻る