群馬大学(医学) 2024年　問題4


$以下の問に答えよ。$
$(1)\ \ 0 \leqq x \leqq \dfrac{\pi}{2} \ の範囲において、2\ つの関数 \ y=|\cos x|,\ \ y=|\cos 2x| \ のグラフのみで囲まれた部分の面積$
$\quad および \ 2\ つの関数 \ y=|\cos x|,\ \ y=|\cos 2x|\ のグラフと直線 \ x=\dfrac{\pi}{2} \ で囲まれた部分の面積の和を求めよ。$
$(2)\ \ 0 \leqq x \leqq \dfrac{\pi}{2} \ の範囲において、2\ つの関数 \ y=\cos x,\ \ y=\cos 2x \ のグラフと直線 \ x=\dfrac{\pi}{2} \ で囲まれた部分を$
$\quad x\ 軸のまらりに \ 1\ 回転させてできる立体の体積を求めよ。$


(1)


$0 \leqq x \leqq \dfrac{\pi}{2} \ の範囲において$

$y=\cos 2x \ と \ x\ 軸の交点は \quad \cos 2x=0 \ \ より \ \ 2x=\cfrac{\pi}{2} \qquad x=\cfrac{\pi}{4}$

$y=\cos x \ と \ y=-\cos 2x \ の交点は \quad \cos x=-\cos 2x \qquad \cos x=-(2\cos ^2x -1)$

$2\cos ^2x +\cos x -1=0 \qquad (2\cos x -1)(\cos x +1)=0$

$\cos x=\cfrac{1}{2} \quad より \quad x=\cfrac{\pi}{3}$

　

$2\ つのグラフは右図のようになるから、 y=|\cos x|,\ \ y=|\cos 2x| \ の$

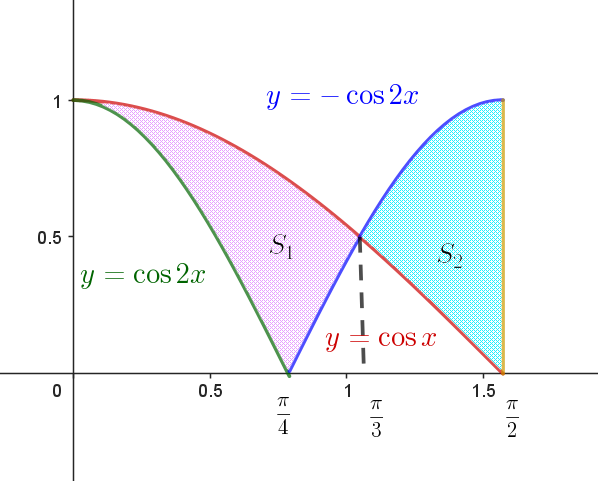
$グラフのみで囲まれた部分の面積を \ S_1,\ \ y=|\cos x|,\ \ y=|\cos 2x|\ の$

$グラフと直線 \ x=\dfrac{\pi}{2} \ で囲まれた部分の面積を \ S_2\ とおくと$

\begin{eqnarray*} S_1 &=&\int_0^{{\scriptsize\dfrac{\pi}{4}}}(\cos x -\cos 2x)dx +\int_{{\scriptsize\dfrac{\pi}{4}}}^{{\scriptsize\dfrac{\pi}{3}}}(\cos x +\cos 2x)dx \\ \\ &=&\int_0^{{\scriptsize\dfrac{\pi}{4}}}\cos xdx - \int_0^{{\scriptsize\dfrac{\pi}{4}}}\cos 2xdx + \int_{{\scriptsize\dfrac{\pi}{4}}}^{{\scriptsize\dfrac{\pi}{3}}}\cos x dx + \int_{{\scriptsize\dfrac{\pi}{4}}}^{{\scriptsize\dfrac{\pi}{3}}} \cos 2xdx \\ \\ &=&\int_0^{{\scriptsize\dfrac{\pi}{3}}}\cos x dx - \int_0^{{\scriptsize\dfrac{\pi}{4}}} \cos 2x dx +\int_{{\scriptsize\dfrac{\pi}{4}}}^{{\scriptsize\dfrac{\pi}{3}}} \cos 2xdx \\ \\ &=&\big[\sin x \big]_0^{{\scriptsize\dfrac{\pi}{3}}} - \cfrac{1}{2}\big[ \sin 2x\big]_0^{{\scriptsize\dfrac{\pi}{4}}} + \cfrac{1}{2}\big[\sin 2x \big]_{{\scriptsize\dfrac{\pi}{4}}}^{{\scriptsize\dfrac{\pi}{3}}}\\ \\ &=&\cfrac{\sqrt{3}}{2}-\cfrac{1}{2} \times 1 + \cfrac{1}{2}(\cfrac{\sqrt{3}}{2}-1)\\ \\ &=&\cfrac{3\sqrt{3}}{4}-1 \end{eqnarray*}
\begin{eqnarray*} S_2 &=&\int_{{\scriptsize\dfrac{\pi}{3}}}^{{\scriptsize\dfrac{\pi}{2}}}(-\cos 2x -\cos x)dx \\ \\ &=&\big[-\cfrac{1}{2} \sin 2x -\sin x ]_{{\scriptsize\dfrac{\pi}{3}}}^{{\scriptsize\dfrac{\pi}{2}}}\\ \\ &=&-1 + (\cfrac{\sqrt{3}}{4}+ \cfrac{\sqrt{3}}{2})\\ \\ &=&\cfrac{3\sqrt{3}}{4}-1 \end{eqnarray*} $よって$

$S_1+S_2=\big(\cfrac{3\sqrt{3}}{4}-1\big)+\big(\cfrac{3\sqrt{3}}{4}-1\big) =\cfrac{3\sqrt{3}}{2}-2$


(2)

　

$右の図は回転体を \ xy\ 平面で切断した断面図である。$

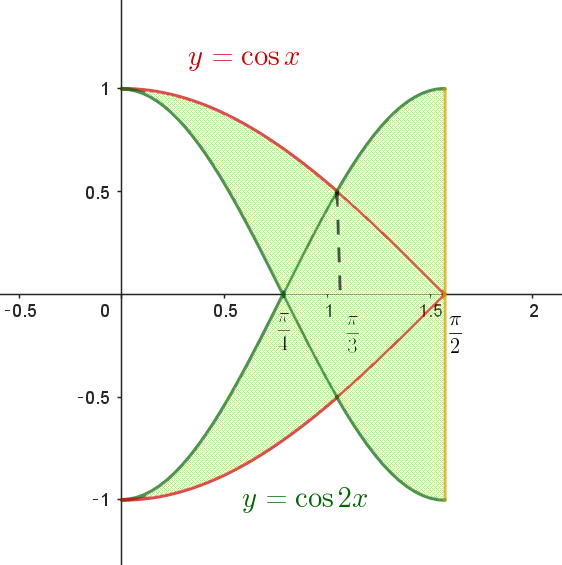
\begin{eqnarray*} V &=&\pi \int_0^{{\scriptsize\dfrac{\pi}{3}}}\cos ^2x dx - \pi \int_0^{{\scriptsize\dfrac{\pi}{4}}} \cos ^2 2x dx + \pi \int_{{\scriptsize\dfrac{\pi}{3}}}^{{\scriptsize\dfrac{\pi}{2}}} \cos ^2 2xdx \\ \\ &=&\cfrac{\pi}{2} \int_0^{{\scriptsize\dfrac{\pi}{3}}}(1+\cos 2x) dx -\cfrac{ \pi}{2} \int_0^{{\scriptsize\dfrac{\pi}{4}}} (1+\cos 4x) dx +\\ \\ & &\qquad \cfrac{\pi}{2} \int_{{\scriptsize\dfrac{\pi}{3}}}^{{\scriptsize\dfrac{\pi}{2}}} (1+\cos 4x)dx \\ \\ &=&\cfrac{\pi}{2}\big[x+\dfrac{1}{2}\sin 2x \big]_0^{{\scriptsize\dfrac{\pi}{3}}} - \cfrac{ \pi}{2} \big[x+\dfrac{1}{4}\sin 4x\big]_0^{{\scriptsize\dfrac{\pi}{4}}} + \cfrac{\pi}{2} \big[x+\dfrac{1}{4}\sin 4x\big]_{{\scriptsize\dfrac{\pi}{3}}}^{{\scriptsize\dfrac{\pi}{2}}} \\ \\ &=&\cfrac{\pi}{2}\big(\dfrac{\pi}{3}+ \dfrac{1}{2} \times \dfrac{\sqrt{3}}{2}\big) - \cfrac{ \pi}{2} \times \dfrac{\pi}{4} + \cfrac{\pi}{2} \big\{\dfrac{\pi}{2}- (\dfrac{\pi}{3}+ \dfrac{1}{4} \times \big(-\dfrac{\sqrt{3}}{2}) \big)\big\}\\ \\ &=&\cfrac{\pi}{16}(3\sqrt{3} + 2\pi )\\ \end{eqnarray*}

ページの先頭へ↑




メインメニュー　に戻る